分块个数就是交点个数 + 1
那么找到交点个数即可
我们把每一个up或者down看成区间修改,然后对于left或者right看成单点查询
也就是说,每一个up和down进行区间修改 + 1,然后对于每一个left和right进行单点查询,查看交点个数即可
比如这个图,把1 1 U这个当成区间修改,把y = 1到y = INF都进行 + 1操作,那么对于2 2 L,只需要查询y = 2这个点的值为几即可。
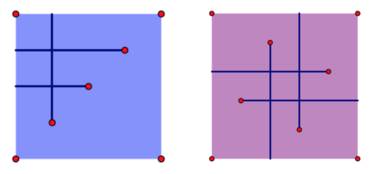
但需要先进行排序,按照x进行从小到大排序,那么对于L的查询,需要从小到大遍历,因为我的射线向左边的,需要把x小的先进行修改
对于R的查询,需要从大到小的查询,因为我的射线是向右边的,需要先把x轴大的先进行修改
- 离散化
- 区间加法
- 单点查询
#include <iostream>
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
const int N = 1e5;
struct Tree{
int l, r, sum;
#define l(p) tree[p].l
#define r(p) tree[p].r
#define sum(p) tree[p].sum
#define lson(p) p << 1
#define rson(p) p << 1 | 1
} tree[N * 4 + 100];
void build(int p, int l, int r) {
l(p) = l; r(p) = r; sum(p) = 0;
if(l == r) return;
int mid = (l + r) >> 1;
build(lson(p), l, mid);
build(rson(p), mid + 1, r);
}
void pushdown(int p){
if(sum(p)) {
sum(lson(p)) += sum(p);
sum(rson(p)) += sum(p);
sum(p) = 0;
}
}
ll Query(int p, int k){
if(l(p) == r(p)){
return sum(p);
}
pushdown(p);
int mid = (l(p) + r(p)) >> 1;
if(k <= mid)return Query(lson(p), k);
else return Query(rson(p), k);
}
void Modify(int p, int l, int r, int c) {
if(l(p) >= l && r(p) <= r) {
sum(p) += c; return;
}
pushdown(p);
int mid = (l(p) + r(p)) >> 1;
if(l <= mid) Modify(lson(p), l, r, c);
if(r > mid) Modify(rson(p), l, r, c);
}
struct Point{
int x, y;
char op;
bool operator < (const Point &b) const{
return x < b.x;
}
} p[N];
int a[N], b[N]; // 离散化
void solve(){
int n, m, k;
scanf("%d%d%d", &n, &m, &k);
for(int i = 1; i <= k; i++){
scanf("%d%d %c", &p[i].x, &p[i].y, &p[i].op);
a[i] = p[i].x, b[i] = p[i].y;
}
sort(a + 1, a + k + 1); sort(b + 1, b + k + 1);
int am = unique(a + 1, a + k + 1) - a - 1;
int bm = unique(b + 1, b + k + 1) - b - 1;
for(int i = 1; i <= k; i++) {
p[i].x = lower_bound(a + 1, a + am + 1, p[i].x) - a;
p[i].y = lower_bound(b + 1, b + bm + 1, p[i].y) - b;
}
sort(p + 1, p + k + 1);
build(1, 1, N);
ll ans = 1;
for(int i = 1; i <= k; i++) {
if(p[i].op == 'D') Modify(1, 1, p[i].y, 1);
if(p[i].op == 'U') Modify(1, p[i].y, N, 1);
if(p[i].op == 'L') ans += Query(1, p[i].y);
}
build(1, 1, N);
for(int i = k; i >= 1; i--) {
if(p[i].op == 'D') Modify(1, 1, p[i].y, 1);
if(p[i].op == 'U') Modify(1, p[i].y, N , 1);
if(p[i].op == 'R') ans += Query(1, p[i].y);
}
printf("%lld
", ans);
}
int main(){
int t; scanf("%d", &t);
while(t--) solve();
return 0;
}
cf类似的题
不同的地方在于是线段进行分割而不是射线
同理,分块数 = 交点数 + 1
此时注意一下,如果说有一条线段是连接两条边的,即直接把矩阵分成两块的,也算是一个交点