TREAP
treap(树堆)是指有一个随机附加值满足堆的性质的二叉搜索树,基本操作期望时间复杂度为O(logn),相比于其他平衡树,treap实现较简单,且能实现随机平衡。
在这里我就讲下小根堆的treap(大根堆一样),treap在SBT的性质上还附加了一个随机值(优先级),小根堆的话,当前节点的优先级一定小于其子树中的优先级;
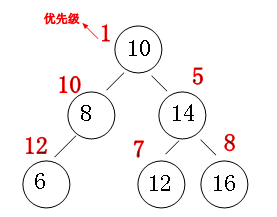
像上面就是一棵(小根堆)treap;
插入操作:按造要插入的数的KEY值来决定它要往当前节点的右子树走还是左子树走,找到合适位置后再来考虑它的随机值,维护堆的性质,递归实现即可;
旋转操作:其实和SBT是一样的:当我们插入一个数,在找到它的位置过程中,它的随机值可能不满足堆的性质,若它的随机值小于当前节点,我们需根据它的位置来进行相应
的左旋或右旋;
删除操作:删除值为x的值,从根开始找,找到x值后,我们需把它旋到叶子节点才能进行删除,通过判断x值的左右子树节点的随机值旋转,若x.l.rd<x.r.rd,进行右旋,否则左旋;
这些就是基本的操作啦,求前驱后继就不用我讲了吧;
luogu 3369:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 using namespace std; 5 6 struct TREAP{ 7 int l,r,val,sz,recy,rd; 8 }t[1000000]; 9 10 int m,size,root,ans; 11 12 void update(int k){ 13 t[k].sz=t[t[k].l].sz+t[t[k].r].sz+t[k].recy; 14 } 15 16 void left_rotate(int &k){ 17 int y=t[k].r;t[k].r=t[y].l;t[y].l=k; 18 t[y].sz=t[k].sz;update(k);k=y; 19 } 20 void right_rotate(int &k){ 21 int y=t[k].l;t[k].l=t[y].r;t[y].r=k; 22 t[y].sz=t[k].sz;update(k);k=y; 23 } 24 25 void insert(int &k,int x){ 26 if (k==0){ 27 ++size;k=size;t[k].sz=t[k].recy=1; 28 t[k].val=x;t[k].rd=rand();return ; 29 } 30 ++t[k].sz; 31 if (t[k].val==x) ++t[k].recy; 32 else if (x>t[k].val){ 33 insert(t[k].r,x); 34 if (t[t[k].r].rd<t[k].rd) left_rotate(k); 35 }else{ 36 insert(t[k].l,x); 37 if (t[t[k].l].rd<t[k].rd) right_rotate(k); 38 } 39 } 40 41 void del(int &k,int x){ 42 if (k==0) return ; 43 if (t[k].val==x){ 44 if (t[k].recy>1){ 45 --t[k].recy;--t[k].sz;return ; 46 } 47 if (t[k].l*t[k].r==0) k=t[k].l+t[k].r; 48 else if (t[t[k].l].rd<t[t[k].r].rd) 49 right_rotate(k),del(k,x); 50 else left_rotate(k),del(k,x); 51 } 52 else if (x>t[k].val) 53 --t[k].sz,del(t[k].r,x); 54 else --t[k].sz,del(t[k].l,x); 55 } 56 57 int atrank(int k,int x){ 58 if (k==0) return 0; 59 if (t[k].val==x) return t[t[k].l].sz+1; 60 else if (x>t[k].val) 61 return t[t[k].l].sz+t[k].recy+atrank(t[k].r,x); 62 else return atrank(t[k].l,x); 63 } 64 65 int rerank(int k,int x){ 66 if (k==0) return 0; 67 if (x<=t[t[k].l].sz) return rerank(t[k].l,x); 68 else if (x>t[t[k].l].sz+t[k].recy) 69 return rerank(t[k].r,x-t[k].recy-t[t[k].l].sz); 70 else return t[k].val; 71 } 72 73 void pred(int k,int x){ 74 if (k==0) return ; 75 if (t[k].val<x){ 76 ans=k;pred(t[k].r,x); 77 }else pred(t[k].l,x); 78 } 79 80 void succ(int k,int x){//找后缀 81 if (k==0) return ; 82 if (t[k].val>x){ 83 ans=k;succ(t[k].l,x); 84 }else succ(t[k].r,x); 85 } 86 87 int main(){ 88 int f,x; 89 scanf("%d",&m); 90 for (int i=1;i<=m;++i){ 91 scanf("%d%d",&f,&x);ans=0; 92 if (f==1) insert(root,x); 93 // printf("%d",root); 94 if (f==2) del(root,x); 95 // printf("%d",root); 96 if (f==3) printf("%d ",atrank(root,x)); 97 if (f==4) printf("%d ",rerank(root,x)); 98 if (f==5) {pred(root,x);printf("%d ",t[ans].val);} 99 if (f==6) {succ(root,x);printf("%d ",t[ans].val);} 100 } 101 return 0; 102 }
