A:https://www.nowcoder.com/acm/contest/139/A
题意:小花填矩阵,矩阵大小n*m 每个格子可以填{0,1,2},规则是每个格子里的数字必须小于等于右边格子的数字,并且小于等于下面格子的数字,求填满这个矩阵有多少种办法。数据范围n,m<=1000 测试样例1e5组 时间1s
思路:首先我们开场就开了这道题,但是到最后都没有写出来,队长思路是DP,但是我枚举了一下3*3的情况,发现转移方程行不通,因为每一个点决定着以他为右下角的一个矩阵的情况,这样的话,无论根据上面右边的点转移,还是根据左上角的点转移,前面的状态都有可能产生冲突,所以,转移方程行不通。
这样的话,我们就开始在分界线上下功夫,以简入难,当只能填0,1的时候,我们知道,他们两个之间一定存在一条线,将两部分分开,此时我们入了枚举起点终点的坑,然而,这样的话,起点终点可能在很多个点,几乎是n*m的复杂度,但是暂时忍了,当把第二条线段加进去的时候,发现即使第二条边的起点终点都在第一条边的下面也可能会出现重叠的可怕部分,遂卒,具体当时的想法如下图所示,黄色线代表0,1分界线,绿色线代表1,2分界线
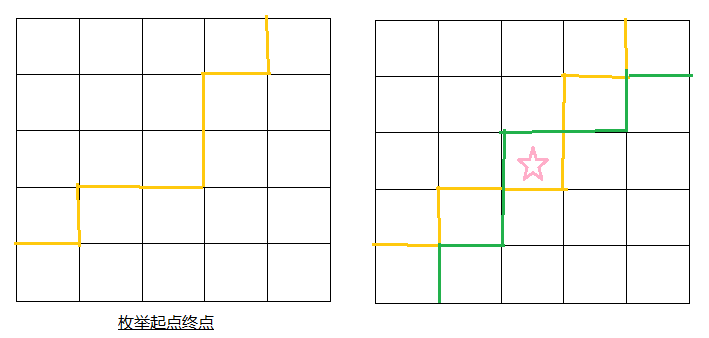
看题解很震惊,如同五月份省赛那天的震惊,因为这个题也是那个题演变来的,首先不需要枚举起点终点,因为每一个起点终点的路径我们都可以转化成从右上角到左下角的一条路径,如图所示
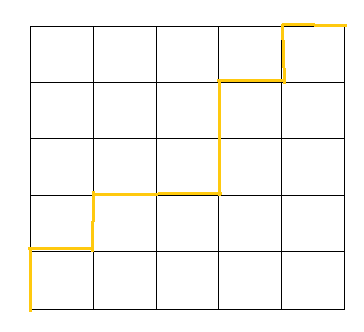
所以,此题就可以转换为求从右上角到左下角的两条完全不相交路径,完全不相交可以考虑到省赛的那道题,但是那道题是起点终点都不同,但是这个是起点终点都相同,怎么办呢,将一条线平移一下,向左上方平移一个格,于是,此题就转换成了省赛的起点终点都不同的两条不相交路径有多少种了,解法就是路径1*路径2-路径3*路径4 (路径3与路径4是路径1 2交换终点之后得到的)
代码如下:
#include<stdio.h> #include<iostream> using namespace std; long long n , m; long long ans; long long tmp; long long c[2010][1006]; const long long mod = 1000000007; void C() { c[1][0] = c[1][1] = 1; for(long long i=2 ; i<=2000; i++) { c[i][0] = 1; for(long long j=1; j<=min(i , (long long)1000); j++) { c[i][j] = (c[i-1][j]+c[i-1][j-1])%mod; } } } int main() { C(); while( scanf("%lld%lld" , &n , &m) != EOF ) { // printf("%lld....%lld.... " , c[2000][1000] , c[2000][999]); tmp = c[n+m][n]; ans = ((tmp*tmp)%mod-(c[n+m][n-1]*c[n+m][m-1])%mod+mod)%mod; printf("%lld " , ans); } return 0; }
D:https://www.nowcoder.com/acm/contest/139/D
题意:给你两个简单图,简单图,顾名思义,没有重边和自回路,于是对于每一条边,我们都可以根据两个端点唯一的进行编号确定,这一点对后面有用。然后给你两个图让你干嘛呢,两个图的点数相同,边数不同,让你从G2图中窜出多少种子图,可以与G1完全一致,点的编号可以不考虑(这在题目中它定义了映射、同构这么个概念,可以忽略),问有多少种子图,点的个数最多是8
思路:8个点,我们枚举所有的映射方式,即8的全排列,8!时间上乐意支持的住,对于每一种映射,假设i号结点映射带G2上的点是ans[i],因为没有自回路与环,对于G1中i,j之间的边,我们可以判断G2中,ans[i] ,ans[j]之间是否有边,如果都有,说明这种映射方式可行,我们就把所选的边的组合方式存起来,因为最多有64条边,所以我们根据long long的每一位来定义一条边,边的编号我们用端点号小的*8+编号大的,可以保证每条边的编号都不同(0~63),因为不同的映射方式,可能选的边是一样的,我们将边的集合转换成一个数字,然后存起来,最后需要去重,我们利用set存,可以完美的减少工作量。
代码如下:
#include<stdio.h> #include<iostream> #include<set> #include<algorithm> #include<string.h> using namespace std; unsigned long long n , m1 , m2; unsigned long long map1[10][10] , map2[10][10]; unsigned long long ans[10]; unsigned long long vis[10]; unsigned long long f[70]; set<long long>qq; void init() { memset(map1 , 0 , sizeof(map1)); memset(map2 , 0 , sizeof(map2)); memset(ans , 0 , sizeof(ans)); memset(vis , 0 , sizeof(vis)); qq.clear(); } void dfs(unsigned long long x) { unsigned long long tmp = 0; // int flag = 1; if(x == n) { // printf(" "); for(unsigned long long i=1; i<=n; i++) { // printf("%lld... " , ans[i]); for(unsigned long long j=1; j<=n; j++) { if(map1[i][j] == 1) { if(map2[ans[i]][ans[j]] != 1) { return ; // flag = 0; } int flag = min(ans[i]-1,ans[j]-1)*8+max(ans[i]-1,ans[j]-1); // printf("%lld...%lld... " , ans[i]-1 , ans[j]-1); // printf("%d.. " , flag); tmp += f[flag]; } } // tmp += f[ans[i]-1]; //不能这么加 这么加会有遗漏 //对边进行编号 编号为两个端点中小的那个值*9+大的那个值 检验可得 这样的编号方式不会有重复 } // printf("....%lld..... " , tmp); // if(flag == 1) qq.insert(tmp); } for(unsigned long long i=1; i<=n; i++) { if(vis[i] == 1) continue; vis[i] = 1; ans[x+1] = i; dfs(x+1); vis[i] = 0; } } void input() { unsigned long long a , b; for(unsigned long long i=1; i<=m1; i++) { scanf("%lld%lld" , &a , &b); map1[a][b] = 1; // map1[b][a] = 1; } for(unsigned long long i=1; i<=m2; i++) { scanf("%lld%lld" , &a , &b); map2[a][b] = 1; map2[b][a] = 1; } } int main() { f[0] = 1; for(int i=1; i<=63; i++) { f[i] = f[i-1]*2; } while( scanf("%lld%lld%lld" , &n , &m1 , &m2) != EOF ) { init(); // printf("..... "); input(); for(unsigned long long i=1; i<=n; i++) { ans[1] = i; vis[i] = 1; dfs(1); vis[i] = 0; } // set<long long>::iterator it; // for(it=qq.begin(); it!=qq.end(); it++) // printf("%lld++++ " , *it); printf("%d " , qq.size()); } return 0; }
J:https://www.nowcoder.com/acm/contest/139/J
题意:给出一个字符串,字符串的长度是1e5,给出1e5次询问,每次询问给你一个区间【L,R】,问你[1,l]+[r,n]区间内有多少个不同的数字
思路:这个题也是省赛一道题的变形,省赛是给出一个连续的区间,求不同的数字由多少个,现在就是将两个断开的区间变成一个连续的区间,办法就是将原数列接一个到后面去,这样的话数列长度就变成了2*n,但是两个区间也可以连在一起去了,于是莫队也好,树状数组也好,主席书也好,搞一波就好了,此处留坑:树状数组与主席书 啊 填坑很困难啊(主席书已填坑)
队长莫队代码如下,此处需要注意,块的大小普通开sqrt(n)是会超时的,我们需要开500以上才可以,我队英勇开了1000,过了,WA了三发,一发编译错误,两发块开小了
我队代码风格都不一样,我的代码运行时间都比队长长,抱队长大腿
#include<stdio.h> #include<string.h> #include<math.h> #include<algorithm> #define rep(i,j,k) for(int i=j;i<=k;++i) using namespace std; struct s { int id,ans; int l,r; } f[100005]; int a[200005],ff[100005]; bool cmp(s aa,s bb) { if(aa.l/1000==bb.l/1000) return aa.r<bb.r; return aa.l<bb.l; } bool cmp1(s aa,s bb) { return aa.id<bb.id; } int sum=0; void add(int x) { if(ff[a[x]]==0) sum++; ff[a[x]]++; } void del(int x) { ff[a[x]]--; if(ff[a[x]]==0) sum--; } int main() { int n,q; while(scanf("%d %d",&n,&q)!=EOF) { memset(ff,0,sizeof(ff)); rep(i,1,n) { scanf("%d",&a[i]); a[i+n]=a[i]; } // rep(i,1,2*n) // printf("%d++++++ ",a[i]); rep(i,0,q-1) { scanf("%d %d",&f[i].l,&f[i].r); f[i].id=i; f[i].l+=n; swap(f[i].l,f[i].r); // printf("%d %d %d+++++++++++++++ ",f[i].id,f[i].l,f[i].r); } sort(f,f+q,cmp); sum=0; int ll=1,rr=0; rep(i,0,q-1) { while(rr<f[i].r) add(++rr); while(ll>f[i].l) add(--ll); while(ll<f[i].l) del(ll++); while(rr>f[i].r) del(rr--); f[i].ans=sum; } sort(f,f+q,cmp1); rep(i,0,q-1) printf("%d ",f[i].ans); } }