一、图的定义:由顶点集和顶点间的关系集合E(边的集合)组成的一种数据结构,用二元组定义为:G1=(V1,E1)。
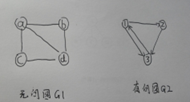
G1、G2的数据结构可以描述为:
1) G1 =(V1,E1),其中
V1 = {a,b,c,d},E1 = {(a,b),(a,c),(a,d),(b,d),(c,d)}
2) G2 = (V2,E2),其中
V2 = {1,2,3},E2={<1,3>,<1,2>,<2,3>,<3,1>}
二、基本术语
1、有向图和无向图—》方向性
2、完全图、稠密图、稀疏图
1)完全图 :
完全无向图:具有n个顶点,n(n-1)/2条边的图
完全有向图:具有n个顶点,n(n-1)条弧的图
一般无向图,顶点数为n,变数为e,啧0<= e <=n(n-1)/2
一般有向图,顶点数为n,变数为e,啧0<= e <=n(n-1)
2) 一个图接近完全图称为稠密图,反之则称为稀疏图
3) 度、出度、入度
一个顶点依附的边或弧的数目,称为该顶点的度。
有向图中,顶点依附的弧头数目称为该顶点的入度。弧尾数目称为出度。入度和出度的和,称为该顶点的度。
三、图的存储结构
顺序存储结构:数组表示法(领接矩阵)
链式存储结构:多重链表(邻接表和邻接多重表)
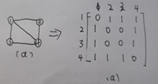
1、 第一类:领接矩阵
1)若(I,j)属于E(G)或 <I,j>属于E(G),则j行i列的元素为1,否则为0
n个顶点的矩阵大小为n*n

2)网(带权值的图称为网)
网的邻接矩阵表示为:
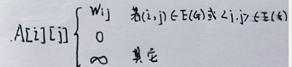
图&网的邻接矩阵数据类型描述
struct mpraph
{ 图中顶点数;
图中边数;
存放顶点信息V1,V2,Vn;
邻接矩阵
}
2、 第二类:邻接表(链式)表示法
对每个顶点Vi建立一个单链表,把与Vi有关联的边的信息链接起来
每个结点设三个域
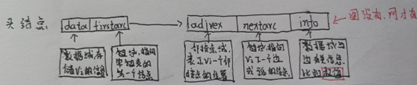
每个单链表有一个头结点(设两个域),存放Vi信息
1)无向图邻接表:

无向图的邻接表不唯一,图各边结点的链入顺序是任意的
2)有向图邻接表:

3、 邻接多重表
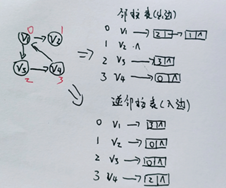
解析:
图有5条边,对应的邻接多重表就是10根线,ivex和jvex就是边的两个结点,ilink指向的是ivex结点的相邻边,jlink则是jvex的结点相邻的边。
四、图的遍历
分为深度优先遍历和广度优先遍历
1、 深度优先遍历
1) 先访问顶点i,并将其标记为访问过,即visited[i]=1;
2) 然后搜索与顶点i有边连结的下一个顶点j,若j未被访问过,则访问它,并将j标记为访问过,即visited[j]=1;,然后从j开始重复此过程,若j已被访问,再看与i有相连接的边的其它顶点。
3) 若与i有相连接的结点都被访问过,则回退一步,重复此过程。
4) 用栈记录访问过的边。
2、 广度优先遍历(队列)
1、 开始时要将其置空
2、 在每访问一个顶点时,要将其入队
3、 在访问一个顶点的所有后继时,要将其出队
4、 若队列空了,则访问完成
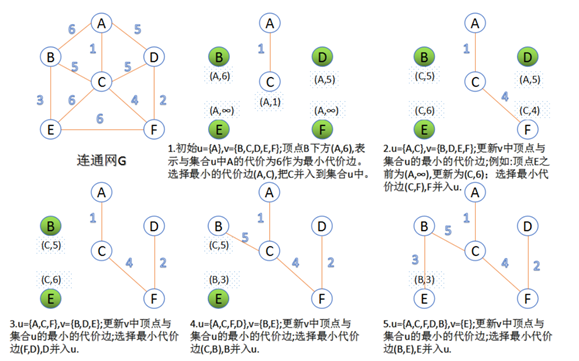
五、最短路径算法
迪杰斯特拉算法:
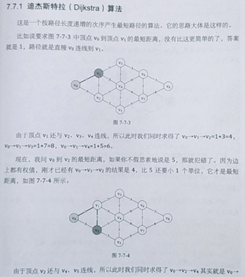

六、拓扑排序
入度为0的结点开始
输出一个入度为0的结点
然后与该结点相连的边消失
这时候得到一个新的图(并不是新的图,为了方便理解)
重新为该图写出邻接表,以此往复 答案也不唯
七、最小生成树
kruskl

prim