2018牛客网暑期ACM多校训练营（第二场）I-car

题意：

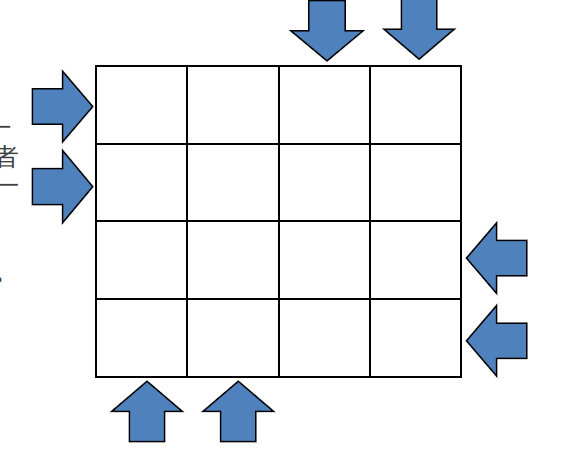
你要在一个n*n的矩形的边界上方若干辆车，所有车从同一
时刻出发，以同样的速度，从某一列的一侧开到另一侧或者
从某一行的一侧开到另一侧。问最多放多少量车使得存在一
种方式，这些车在行驶的过程中互不相撞。
（车可以视为质点）
同时还会有若干个格子被损坏车辆不能开进被损坏的格子。

先考虑所有格子全部完好的情况。
通过爆搜/脑洞，发现答案就是2n-(n mod 2)。
如何证明？
首先，一行一列最多只能放一辆车，同时如果n为奇数，则第(n+1)/2行和第(n+1)/2列不能都放车，所以刚刚
那个值是答案的上界。
同时我们也可以很容易地构造一组满足这个解的方案，得证。
有格子损坏时的情况也不难处理，就把那些行列去掉就好了。

代码：

/*
这题一开始做的时候并没有考虑好车子的分布
该矩阵可以把它分成四个小部分，分别对应相应的方向

*/

#include <bits/stdc++.h>

using namespace std;

const int maxn=1e5+10;

int n,m;
int x,y;
int s1[maxn],s2[maxn];

int main()
{
    cin>>n>>m;
    memset(s1,0,sizeof(s1));
    memset(s2,0,sizeof(s2));
    for(int i=0;i<m;i++)
    {
        cin>>x>>y;
        s1[x]++;
        s2[y]++;
    }
    int ans=2*n-n%2;
    for(int i=1;i<=n;i++)
    {
        if(s1[i]) ans--;
        if(s2[i]) ans--;
    }
     if(n%2==1&&s1[(n+1)/2]==1&&s2[(n+1)/2]==1) ans++;///多减了一次
    cout<<ans<<endl;
    return 0;
}