P1
题目描述:
给出一个二分图,选择互不相交的边,使得边覆盖的点权和最大。
solution:
简单DP,用树状数组维护最大值。
时间复杂度:$O(n log n) $
P2
题目描述:
给出N个或黑或白的元素,每个元素有与A集合和B集合相对应的A,B两个值,将N个元素分成A,B两个集合,使每个集合的前K大中的黑色元素的总和最大。
solution:
因为每个元素都有两个关键字,而且每个关键字只对对应的集合有用,所以必须对其中一个关键字进行固定。枚举A集合的第K大是哪个元素(i),因为只需要黑色元素总和最大,所以A值比A[i]大的黑色元素都归到A集合,A值比A[i]小的白色元素也归到A集合(防止该元素是B集合的前K大)。然后对黑色元素和剩下的白色元素进行DP,状态f[p][q]表示到前p个元素有q个元素分到了A集合的最大值。
时间复杂度:$ O(n^3) $
P3
题目描述:
给定一棵树。在线求路径点序列u -> ... -> v1,连续子序列a1,a2 ... ak满足a1<a2< ... <aj>aj+1 >aj+2 >.....>ak或者a1>a2>... >aj< aj+1<aj+2<.... <ak,1<=j<=k,求最大的 (k)。
solution:
关于树的算法不多,这题LCA就可以了,只是如何实现合并而已,我们对于LCA的每个区间记12个域:
区间左端:
- 递增
- 递减
- 先增后减
- 先减后增
区间右端:
- 递增
- 递减
- 先增后减
- 先减后增
- 区间左端编号
- 区间右端编号
- 区间长度
- 最大值
至于转移方程嘛……,自己推。
时间复杂度:$ O(n log n) $
P4
题目描述:
给出一个一开始为0的无穷栈,每次从栈顶拿出一个数(top),并把栈里剩下的元素最低位变成$ (Y+1) mod K ((Y为之前的最低位),然后用top与L相比,如果) top < L (,那么X减一,否则把)top+AK(复制K份放入栈中。当)X=0$时,结束操作,输出top。
solution:
这题的数据很大,因此应该是找规律的题目。观察可得,栈里面的数的变化只与出栈次数有关,如果要把栈里的某一个元素出栈,必须经历s次出栈,而( s%K=1).
令$ L=cAK+d (,而栈里的数i只可能是) i=pAK+p,(0leq pleq c+1, 0leq qleq d) (因此我们可以寻找循环节。例如)K=5,L=21,A=2$

这表格包含了所有可能的数字,从纵向来看,它代表某一个数加AK的值,横向来看,它代表每个数的变化。红色为死亡濒临线。对于第二行(从下向上数)的数来说,必须死13次才能将其出栈,对于第一行来说,必须要死135次才能将其出栈。如果要将第一行的全部出栈,必须死$ 135^2 $次。
再举一个例子:(K=5,L=26,A=2)
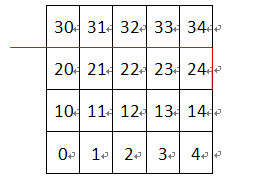
对于第三行要5次,第二行(52),第三行(53),……
再利用第一个例子研究答案:
30 31 32 33 34 * 31 32 33 34 30 * 22 23 24 *
31 32 33 34 30 * 22 23 24 * 30 31 32 33 34 *
22 23 24 * 30 31 32 33 34 * 31 32 33 34 30 *
23 24 * 30 31 32 33 34 * 31 32 33 34 30 * 22
24 * 30 31 32 33 34 * 31 32 33 34 30 * 22 23
31 32 33 34 30 * 22 23 24 * 30 31 32 33 34 *
22 23 24 * 30 31 32 33 34 * 31 32 33 34 30 *
23 24 * 30 31 32 33 34 * 31 32 33 34 30 * 22
24 * 30 31 32 33 34 * 31 32 33 34 30 * 22 23
30 31 32 33 34 * 31 32 33 34 30 * 22 23 24 *
22 23 24 * 30 31 32 33 34 * 31 32 33 34 30 *
23 24 * 30 31 32 33 34 * 31 32 33 34 30 * 22
24 * 30 31 32 33 34 * 31 32 33 34 30 * 22 23
30 31 32 33 34 * 31 32 33 34 30 * 22 23 24 *
31 32 33 34 30 * 22 23 24 * 30 31 32 33 34 *
……
规律显得,
当d<K时,每行有( (d+1)K+(K-d-1) )个元素,每一部分为一行出栈的死亡情况,所以答案的循环节(即整个表格死一次)为( ((d+1)K+(K-d-1))K^c )
算答案时令( t=(d+1)K+(K-d-1) ),把X拆成( X=a_{0}+sum_{i=1}{c}a_{i}tK{i-1} ),通过( (sum_{i=1}^{c}a_{i})%K )算出答案所在行,再利用( a_{0} )确定列。
当d>=K时,每行有K个元素,所以答案的循环节为( K^(c+2) ),计算答案就想一想好了。
废话不说(我也解释不清),上代码(和链接)
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <ctime>
#include <queue>
#include <deque>
#include <map>
#include <vector>
using namespace std;
typedef long long LL;
const LL oo=1e18;
int T;
LL X, K, L, A;
int main()
{
freopen("avenger.in", "r", stdin);
freopen("avenger.out", "w", stdout);
scanf("%d", &T);
while (T--)
{
scanf("%I64d%I64d%I64d%I64d", &X, &K, &L, &A);
LL AK=A*K;
LL c=L/AK, d=L-AK*c;
LL ans=0;
if (d>=K-1)
{
--X;
for (int i=1; X && i<=c+2; X/=K, ++i)
ans=(ans+X%K)%K;
printf("%I64d
", (c+1)*AK+ans);
}
else
{
LL t=(d+1)*K+(K-d-1);
--X;
LL a0=X%t;
X/=t;
for (int i=1; X && i<=c; X/=K, ++i)
ans=(ans+X%K)%K;
if (ans<d+1)//the last is in the front最后一行在前
{
if (a0<(d-ans+1)*K)//the last
{
LL tmp=a0%K;
a0/=K;
printf("%I64d
", (c+1)*AK+(ans+a0+tmp)%K);
}
else//the last but one倒数第二行
{
a0-=(d+1-ans)*K;
if (a0<K-1-d) printf("%I64d
", c*AK+d+1+a0);
else//the last最后一行
{
a0-=(K-1-d);
printf("%I64d
", (c+1)*AK+(a0%K+a0/K)%K);
}
}
}
else//the last but one is in the front倒数第二行在前
{
if (a0<(K-d-1)-(ans-d)+1)
printf("%I64d
", c*AK+a0+ans);
else//the last最后一行
{
a0-=(K-d-1)-(ans-d)+1;
if (a0<K*(d+1))
printf("%I64d
", (c+1)*AK+(a0/K+a0%K)%K);
else//the last but one倒数第二行
{
a0-=K*(d+1);
printf("%I64d
", c*AK+d+1+a0);
}
}
}
}
}
return 0;
}