利用ARIMA算法建立短期预测模型

　　周五福利日活动是电信为回馈老用户而做的活动，其主要回馈老用户的方式是让用户免费领取对应的优惠券，意在提升老用户的忠诚度和活跃度。今日，为保证仓库备货优惠券资源充足，特别是5元话费券等，需要对该类优惠券领取效果进行预测，从而指导备货。经研究选用ARIMA算法建立预测模型，对5元话费券进行日领取量的短期预测。数据集收集了2019年1月到2019年2月5元话费券的日领取量数据，并根据此数据做时间序列分析并建立预测模型。

　　1、进行数据的加载

from statsmodels.tsa.stattools import acf, pacf
import statsmodels.api as sm
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.stats as stats

receive=pd.read_excel(r'E:EringdataHF_5.xlsx')

　　2、进行一阶差分和检验一阶差分的效果

#设置一下时间索引并进行一阶差分
receive.index=pd.Index(pd.date_range('1/1/2019','31/3/2019',freq='1D'))
receive['number'].plot()
receive['number'].diff(1).plot() 

　　利用自相关系数的白噪声检验差分效果

# 利用自相关系数的白噪声检验差分后的数据是否是平稳序列：
r,q,p=sm.tsa.acf(receive['number'].diff(1).iloc[1:92].values.squeeze(),qstat=True) #squeeze: 除去size为1的维度
mat=np.c_[range(1,41),r[1:],q,p] #np.c_是按行连接两个矩阵，把两矩阵左右相加，要求行数相等，类似pandas的merge()
table=pd.DataFrame(mat,columns=['lag','AC','Q','Prob(>Q)'])
LB_result=table.iloc[[5,11,17]]
LB_result.set_index('lag',inplace=True)
LB_result

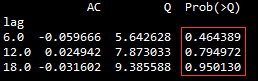
　　上图是自相关系数白噪声检验的结果，P值均大于0.05，表明白噪声检验不显著，所以数据经过一阶差分后平稳，故此知道一阶差分后所形成的序列是平稳序列。ARIMA算法的一个重要应用前提是保证算法入口的数据是平稳的。差分阶次对应ARIMA（p,d,q）中的d数值，因此本文中的d可以设置为1。

　　3、确定系数p和q

# 利用BIC最小的模型作为识别的依据,确定参数p和参数q：
order_p,order_q,bic=[],[],[]
model_order=pd.DataFrame()
for p in range(4):
    for q in range(4):
        arma_model=sm.tsa.ARMA(receive['number'].diff(1).iloc[1:89].dropna(),
                               (p,q)).fit()
        order_p.append(p)
        order_q.append(q)
        bic.append(arma_model.bic)
        print('The BIC of ARMA(%s,%s) is %s'%(p,q,arma_model.bic))

model_order['p']=order_p
model_order['q']=order_q
model_order['BIC']=bic
P=list(model_order['p'][model_order['BIC']==model_order['BIC'].min()])
Q=list(model_order['q'][model_order['BIC']==model_order['BIC'].min()])
print('最好的模型是ARMA(%s,%s)' %(P[0],Q[0]))

　　

　　根据BIC法则确定可知，当p值和q值分别为1和0的时候，可以取到模型的效果最好。

　　4、建立ARIMA预测模型

#建立ARIMA模型
model=sm.tsa.ARMA(receive['number'].diff(1).iloc[1:89].dropna(),(1,0)).fit(method='css') #使用最小二乘，‘mle’是极大似然估计
#画图比较一下预测值和真实观测值之间的关系
fig=plt.figure(figsize=(8,6))
ax=fig.add_subplot(111)
ax.plot(receive['number'].diff(1).iloc[1:89],color='blue',label='number')
ax.plot(model.fittedvalues,color='red',label='Predicted number')
plt.legend(loc='lower right')

　　

　　5、差分值转化为原始值

# 差分数据转化为原始值
def forecast(step,var,modelname):
    diff=list(modelname.predict(len(var)-1,len(var)-1+step,dynamic=True))
    prediction=[]
    prediction.append(var[len(var)-1])
    seq=[]
    seq.append(var[len(var)-1])
    seq.extend(diff)
    for i in range(step):
        v=prediction[i]+seq[i+1]
        prediction.append(v)

    prediction=pd.DataFrame({'Predicted number':prediction})
    return prediction[1:]  #第一个值是原序列最后一个值，故第二个值是预测值。
forecast(15,receive['number'][1:89],model)

　　如图是4月1-5号的预测值。

　　6、模型残差项的白噪声检验及正态性检验

# 模型残差项的白噪声检验：
resid=model.resid
r,q,p=sm.tsa.acf(resid.values.squeeze(),qstat=True)
mat_res=np.c_[range(1,41),r[1:],q,p] #np.c_是按行连接两个矩阵，把两矩阵左右相加，要求行数相等，类似pandas的merge()
table=pd.DataFrame(mat_res,columns=['to lag','AC','Q','Prob(>Q)'])
LB_result_res=table.iloc[[5,11,17,23]]
LB_result_res.set_index('to lag',inplace=True)
LB_result_res

　　

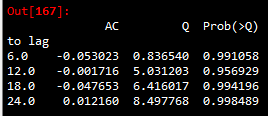
　　如果ARMA模型估计的好，应当使得估计值后的残差项是白噪声。上图是预测结果的残差的白噪声检验结果，分析可知Prob值均较大，查阅资料显示Prob值较大时，接受原假设-残差是白噪声Prob值接近于0时拒绝原假设；接近于1时接受原假设；Prob值为10%时，表示10%置信区间下通过。

　　至此模型建立完毕。