Data Structure and Algorithms Analysis in C Note (I)

 

Four basic rules of recursion:

• Base cases
• Making progress
• Design rules: Assume that all recursive calls work.
• Compound Interest Rule: Never duplicate work by solving the same instance of a problem in separate recursive calls.

Two most common ways of proving statements: by induction and by contradiction.

 

Modular Arithmetic:
A is congruent to B modulo N, written A ≡ B if N divides A – B(The remainder is the same when either A or B is divide by N.).

 

The term procedure refers to a function that returns void.

 

[X] is the largest integer that is less than or equal to X.

 

log X < X for all X > 0;     log2 = 1;     log1024 = 10;     log1048576 = 20.

 

Positive Constants: c, n0.         Precondition: N >= n0

1. T(N) = O(f(N)) such that T(N) <= cf(N)
2. T(N) = Ω(g(N)) such that T(N) >= cg(N)
3. T(N) = Θ(h(N)) if and only if T(N) = Θ(h(N)) and T(N) =Ω(h(N))
4. T(N) = o(p(N)) if T(N) = O(p(N)) and T(N) ≠ Θ(h(N))

Rule 1:

If T1(N) = O(f(N)) and T2(N) = O(g(N)), then

1. T1(N) + T2(N) = max(O(f(N)), O(g(N))
2. T1(N) * T2(N) = O(f(N) * g(N))

log平方——log-squared;        N——Linear;    

2的n次方——exponential;    N的2次方——quadratic;    

N的3次方——cubic;         k次多项式——polynomial of degree k.

Rule 2:

 

If T(N) is polynomial of degree k, then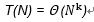

 

Rule 3:

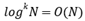for any constant k.

 

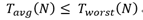
Generally, the quantity required is the worst-case time.

 

Efficient Algorithms: Time to read the input > Time required to solve the problem.

 

Big-Oh is the upper bound; Ω is a lower bound.

 

General rules:

• For loops: Running time = statements inside the for loop (including tests) * the number of iterations

  /* Ignore the costs of calling the function and returning. */

• Nested for loops: Analyze inside out.
• If / Else:

  if (Condition)
  
      S1;
  
  else
  
      S2;

  The running time <= The running time of the test + the larger of S1/S2

If there are function calls, these must be analyzed first.

 

When recursion is properly used, it's difficult to convert the recursion into a simple loop structure.

 

Don't compute anything more than once.

 

Divide and Conquer Strategy:

• Divide part: to split the problem into 2 roughly equal subproblems.
• Conquer stage: patch together the 2 solutions of the subproblems to arrive at a solution for the whole problem.

An algorithm is O(logN) if it takes constant O(1) time to the problem size by a fraction (usually 1/2); if constant time is required to merely reduce the problem by a constant amount, then the algorithm is O(N).

 

Theorem: If M > N, then M mod N < M/2.

 

Checking your analysis:

• Code up the program and observe the running time.
• Verify some program is O(f(N)) is to compute the T(N)/f(N) for a range of N.

  Computed Value : N+ (f(N) is tight), 0 (overestimate), ∞ ( wrong/underestimate)

Overestimate?

1. Needs to be tightened
2. Significantly less than the worst running time and no improvement in the bound is possible.