DAG有向无环图 拓扑排序(207,208)
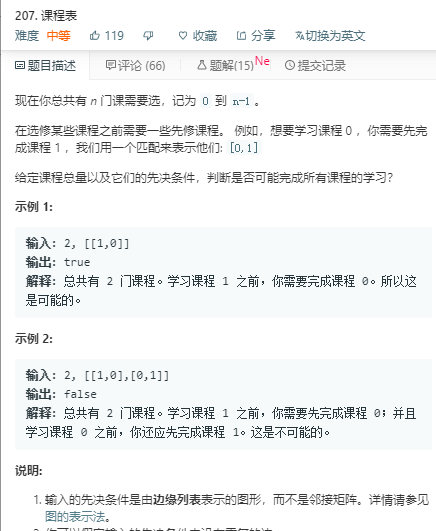
拓扑排序判断有无环。判断是否是有向无环图
方法1:DFS

思路:(自己多在演草纸上想想,把所有演草纸收集起来!)
题解:https://chenzhuo.blog.csdn.net/article/details/91127897
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> flag(numCourses,0);
vector<vector<int>> tmp(numCourses);
if(prerequisites.empty()) return true;
for(int i=0;i<prerequisites.size();i++){
tmp[prerequisites[i][0]].push_back(prerequisites[i][1]);
}
bool ans=true;
for(int i=0;i<numCourses;i++){
ans = ans&&DFS(i,flag,tmp);
}
return ans;
}
bool DFS(int i,vector<int> &flag,vector<vector<int>> &tmp){//注意要加上"&"
if(flag[i]==-1){
return false;
}
if(flag[i]==1){
return true;
}
//第一次的入口:
flag[i]=-1;
for(int j=0;j<tmp[i].size();j++){
if(DFS(tmp[i][j],flag,tmp)){
continue;
}
return false;
}
flag[i]=1;
return true;
}
};
解法2:
方法二:根据入度判断
课程先后顺序可以理解为一个有向图,有解的条件是此图无环。因此我们可以依据其先后顺序构造有向图,并统计每门课程的入度(即其前一门课程的数量)。
然后将入度为0的所有课程压入栈中,然后将这些课程的下一门课程的入度减1,减完后入度为0则入栈。重复上述操作直到栈为空。 如果最后存在入度不为为0的节点就说明有环,无解。
《算法笔记》也有这个算法
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> indegree(numCourses);
vector<vector<int>>Graph(numCourses);
queue<int> ZeroQ;
vector<int> ans,empty;//结果数组
int i,j,cnt=0;
int start,end;
//初始化邻接矩阵
for(i=0;i<prerequisites.size();i++){
start=prerequisites[i][0];
end=prerequisites[i][1];
Graph[end].push_back(start);
indegree[start]++;
}
//初始化队列
for(i=0;i<numCourses;i++){
if(indegree[i]==0){
ZeroQ.push(i);
}
}
while(!ZeroQ.empty()){
int v=ZeroQ.front();
ans.push_back(v);
ZeroQ.pop();
cnt++;
for(j=0;j<Graph[v].size();j++){
int u=Graph[v][j];
indegree[u]--;
if(indegree[u]==0){
ZeroQ.push(u);
}
}
}
if(cnt!=numCourses){
return false;
}
return true;
}
};
2019-09-28 09:44:28
简化到不能再简

class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> G(numCourses);
vector<int> degree(numCourses, 0), bfs;
for (auto& e : prerequisites)
G[e[1]].push_back(e[0]), degree[e[0]]++;
for (int i = 0; i < numCourses; ++i) if (!degree[i]) bfs.push_back(i);
for (int i = 0; i < bfs.size(); ++i)
for (int j: G[bfs[i]])
if (--degree[j] == 0) bfs.push_back(j);
return bfs.size() == numCourses;
}
};
第二天:

class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> graph(numCourses);
vector<int> inDegree(numCourses,0);
for(auto& edge : prerequisites){
graph[edge[1]].push_back(edge[0]);
++inDegree[edge[0]];
}
vector<int> result;
for(int i=0;i<numCourses;++i){
if(inDegree[i]==0) result.push_back(i);
}
for(int i=0;i<result.size();++i){
for(auto j : graph[result[i]]){
if(--inDegree[j]==0) result.push_back(j);
}
}
return result.size()==numCourses;
}
};
还是把自己想得太厉害了。然而自己并不能过目不忘。还是要多敲代码,多巩固,真的感觉到了如果能把自己做过的题保证大部分能做对,真的已经很厉害了。


这个题的代码和上个题完全一样。只是输出换了。
解法1:
队列
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> indegree(numCourses);
vector<vector<int>>Graph(numCourses);
queue<int> ZeroQ;
vector<int> ans,empty;//结果数组
if(numCourses==1){
empty.push_back(0);
return empty;
}
int i,j,cnt=0;
int start,end;
//初始化邻接矩阵
for(i=0;i<prerequisites.size();i++){
start=prerequisites[i][0];
end=prerequisites[i][1];
Graph[end].push_back(start);
indegree[start]++;
}
//初始化队列
for(i=0;i<numCourses;i++){
if(indegree[i]==0){
ZeroQ.push(i);
}
}
while(!ZeroQ.empty()){
int v=ZeroQ.front();
ans.push_back(v);
ZeroQ.pop();
cnt++;
for(j=0;j<Graph[v].size();j++){
int u=Graph[v][j];
indegree[u]--;
if(indegree[u]==0){
ZeroQ.push(u);
}
}
}
if(cnt!=numCourses){
return empty;
}
return ans;
}
};
简化版:
2019-09-28
10:32:15

class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> result;//最优答案
vector<int> empty;//空数组
queue<int> temp;//存储入度为0的节点
if(numCourses==0){
empty.push_back(0);
return empty;
}
vector<vector<int>> graph(numCourses);
vector<int> inDegree(numCourses,0);
for(auto& edge : prerequisites){
graph[edge[1]].push_back(edge[0]);
inDegree[edge[0]]++;
}
for(int i=0;i<numCourses;++i){
if(!inDegree[i]){
temp.push(i);
}
}
int cnt=0;
while(!temp.empty()){
int pre = temp.front();result.push_back(pre);temp.pop();
++cnt;
for(auto i : graph[pre]){
if(--inDegree[i]==0) temp.push(i);
}
}
if(cnt!=numCourses) return empty;
return result;
}
};
2019-09-30
09:21:49

染色问题。
看的评论:采用了贪心算法。
class Solution {
public:
vector<int> gardenNoAdj(int N, vector<vector<int>>& paths) {
vector<vector<int>> result(N);
vector<int> color(N,1);
for(auto path : paths){
result[max(path[0],path[1])-1].push_back(min(path[0],path[1])-1);
}
for(int i=1;i<N;++i){
set<int> set_color{1,2,3,4};
for(int j=0;j<result[i].size();++j){
set_color.erase(color[result[i][j]]);
}
color[i] = *set_color.begin();
}
return color;
}
};
2019-10-04
11:40:54

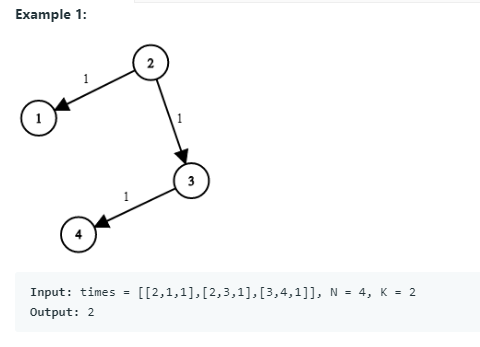
解法1:Dijkstra算法
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
vector<vector<int>> v(N+1,vector<int>(N+1,-1));
for(int i=0;i<times.size();i++){
v[times[i][0]][times[i][1]]=times[i][2];
}
vector<int> S(N+1,-1),T(N+1,-1);
for(int i=1;i<N+1;i++)
T[i]=v[K][i];
T[K]=0;
int min_val=-1,min_idx=-1;
for(int c=0;c<N;c++){
//find min_val of T
min_val=-1;
for(int i=1;i<T.size();i++){
if(T[i]!=-1&&S[i]==-1){
if(min_val==-1||T[i]<min_val){
min_idx=i;
min_val=T[i];
}
}
}
S[min_idx]=min_val;
//update
for(int i=1;i<T.size();i++){
if(v[min_idx][i]!=-1&&(min_val+v[min_idx][i]<T[i]||T[i]==-1)){
T[i]=min_val+v[min_idx][i];
}
}
}
int res=-1;
for(int i=1;i<S.size();i++){
if(S[i]==-1)
return -1;
res=max(res,S[i]);
}
return res;
}
};
解法2:
2019-10-09(第二次)
Bellman-Ford算法


class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
//Bellman-Ford算法
//存储图用邻接表,邻接矩阵需要遍历需要增加O(N)复杂度,将会升为O(N三次方)
vector<int> D(N+1,-1);
D[K] = 0;
for(int c=0;c<N-1;++c){ //只需要N-1 轮就可以,因为D[K] 为0,是已知的
for(int j=0;j<times.size();++j){
int src = times[j][0],des = times[j][1],d = times[j][2];
if(D[src]!=-1&&(D[src]+d<D[des]||D[des]==-1))
D[des]=D[src]+d;
}
}
int res = -1;
for(int i=1;i<D.size();i++){
if(D[i]==-1){
return -1;
}
else res = max(res,D[i]);
}
return res;
}
};
2019-10-05
09:40:27
解法3:
Bellman-Ford 算法的优化版——SPFA(Shorest path Faster Algorithm)算法

class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
vector<vector<int>> v(N+1,vector<int>(N+1,-1));
for(int i=1;i<v.size();++i){
v[i][i]=0;
}
for(int i=0;i<times.size();++i){
v[times[i][0]][times[i][1]] = times[i][2];
}
vector<int> D(N+1,-1);
D[K] = 0;
queue<int> q;
q.push(K);
while(!q.empty()){
auto temp = q.front();
q.pop();
for(int i=1;i<v.size();++i){
if(v[temp][i]!=-1 &&(v[temp][i]+D[temp]<D[i]||D[i]==-1)){
D[i] = v[temp][i] + D[temp];
q.push(i);
}
}
}
int res = 0;
for(int i=1;i<N+1;++i){
if(D[i]==-1){
return -1;
}
res = max(D[i],res);
}
return res;
}
};
解法4:
Floyd 算法,可用来解决全源最短路问题

class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
vector<vector<int>> v(N+1,vector<int>(N+1,-1));
for(int i=1;i<v.size();++i){
v[i][i]=0;
}
for(int i=0;i<times.size();++i){
v[times[i][0]][times[i][1]] = times[i][2];
}
for(int c=1;c<N+1;++c){
for(int i=1;i<N+1;++i){
for(int j=1;j<N+1;++j){
if(v[i][c]!=-1 && v[c][j]!=-1 &&(v[i][c]+v[c][j]<v[i][j]||v[i][j]==-1)){
v[i][j] = v[i][c]+v[c][j];
}
}
}
}
int res = 0;
for(int i=1;i<N+1;++i){
if(v[K][i]==-1){
return -1;
}
res = max(v[K][i],res);
}
return res;
}
};
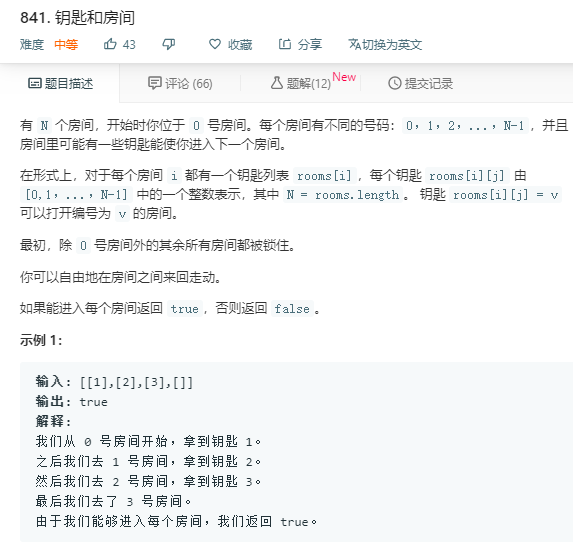
解法1:
自己写的广搜判断是否是连通图


class Solution {
public:
bool canVisitAllRooms(vector<vector<int>>& rooms) {
vector<vector<int>> temp(rooms.size());
for(int i=0;i<rooms.size();++i){//初始化图
for(int j=0;j<rooms[i].size();++j){
temp[i].push_back(rooms[i][j]);
}
}
queue<int> q;
q.push(0);
vector<int> result(rooms.size(),0);
result[0] = 1;
while(!q.empty()){
int c = q.front();
q.pop();
for(auto cnt : temp[c]){
if(result[cnt]!=1){
result[cnt] = 1;
q.push(cnt);
}
}
}
for(int i=0;i<rooms.size();++i){
if(result[i]==0){
return false;
}
}
return true;
}
};
精简版代码:
class Solution {
public:
bool canVisitAllRooms(vector<vector<int>>& rooms) {
queue<int> q;
unordered_set<int> visited;
q.push(0);
visited.insert(0);
while(!q.empty()){
int t = q.front();q.pop();
visited.insert(t);
for(auto key : rooms[t]){
if(visited.count(key)) continue;
q.push(key);
}
}
return visited.size() == rooms.size();
}
};
解法2:DFS
劣质粗糙代码:

class Solution {
public:
int count = 0;
void dfs(int x,int N,vector<int> &visited,vector<vector<int>> rooms){
visited[x] = 1;
++count;
for(int i=0;i<rooms[x].size();++i){
if(!visited[rooms[x][i]]){
dfs(rooms[x][i],N,visited,rooms);
}
}
}
bool canVisitAllRooms(vector<vector<int>>& rooms) {
int N = rooms.size();
vector<int> visited(N,0);
dfs(0,N,visited,rooms);
return count == rooms.size();
}
};

解法1:
自己:
找到出度为0和入度为N-1的点,此点即为法官。
思路:构建一个出度数组和一个入度数组。

class Solution {
public:
int findJudge(int N, vector<vector<int>>& trust) {
vector<int> inDegree(N+1,0);
vector<int> outDegree(N+1,0);
for(auto edge : trust){
inDegree[edge[1]]++;
outDegree[edge[0]]++;
}
for(int i=1;i<N+1;++i){
if(outDegree[i]==0 && inDegree[i]==N-1){
return i;
}
}
return -1;
}
};

解法1:看的评论,自己没想到,自己对DFS的掌握还是不够
思路:DFS染色法,判断拓扑排序中是否有环,并找出不在环内的点(感觉和207,208题有些类似哦,都是判断拓扑排序中是否存在环)
DFS一直往前走,却走回了走过的结点不就是有环了嘛.

代码如下:
#define CIRCLE 1
#define TERMINAL 2
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
int n = graph.size();
vector<int> v(n);
vector<int> cnt;
for(int i=0;i<n;++i){
if(dfs(graph,v,i)==TERMINAL){
cnt.push_back(i);
}
}
return cnt;
}
int dfs(vector<vector<int>>& g,vector<int>& v,int i){
if(v[i]) return v[i];
v[i] = CIRCLE;
for(auto edge : g[i]){
if(dfs(g,v,edge)==CIRCLE){
return CIRCLE;
}
}
return v[i] = TERMINAL;
}
};
解法2:
BFS,和DFS的思路有很大不同。感觉两种方法的着手点是截然不同的。BFS是从入度,出度考虑的。

class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
vector<int> res, outDegree(graph.size(),0);
vector<vector<int>> inDegree(graph.size());
for(int i=0;i<graph.size();++i){//初始化入队的vector<vector<int>>
for(int j : graph[i]){
inDegree[j].push_back(i);
outDegree[i]++;
}
}
for(int i=0;i<graph.size();++i){
if(outDegree[i]==0){
res.push_back(i);
}
}
int idx = 0;
while(idx < res.size()){
int i = res[idx];
++idx;
for(auto j : inDegree[i]){
outDegree[j]--;
if(outDegree[j]==0){
res.push_back(j);
}
}
}
sort(res.begin(),res.end());
return res;
}
};
简化版:
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
vector<int> res, outDegree(graph.size(),0);
vector<vector<int>> inDegree(graph.size());
for(int i=0;i<graph.size();++i){//初始化入队的vector<vector<int>>
for(int j : graph[i]){
inDegree[j].push_back(i);
}
outDegree[i] = graph[i].size();
if(outDegree[i]==0){
res.push_back(i);
}
}
int idx = 0;
while(idx < res.size()){
int i = res[idx];
++idx;
for(auto j : inDegree[i]){
outDegree[j]--;
if(outDegree[j]==0){
res.push_back(j);
}
}
}
sort(res.begin(),res.end());
return res;
}
};
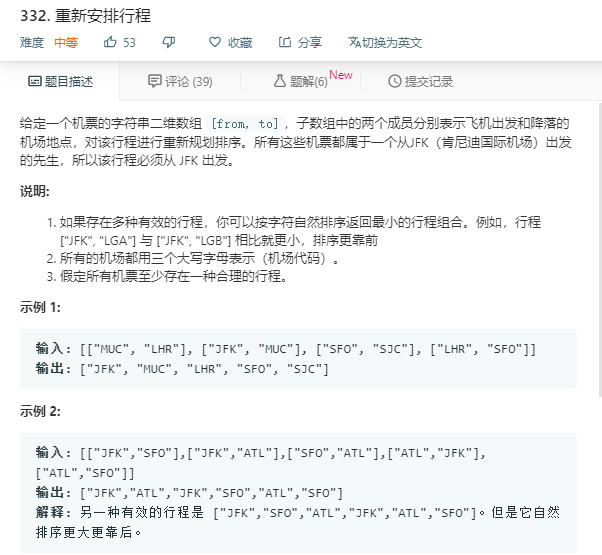
为下面代码做铺垫的新知识:

https://www.cnblogs.com/hustfeiji/articles/5174983.html

这就是说multiset内部是自动排好序的。
解法1:
思路:DFS



class Solution {
public:
map<string, multiset<string>> targets;
vector<string> route;
vector<string> findItinerary(vector<vector<string>>& tickets) {
for (auto ticket : tickets)
targets[ticket[0]].insert(ticket[1]);
visit("JFK");
return vector<string>(route.rbegin(), route.rend());
}
void visit(string airport) {
while (targets[airport].size()) {
string next = *targets[airport].begin();
targets[airport].erase(targets[airport].begin());
visit(next);
}
route.push_back(airport);
}
};
本题是一道树的题目。
就是返回每层各个元素相加和的最大的那个层
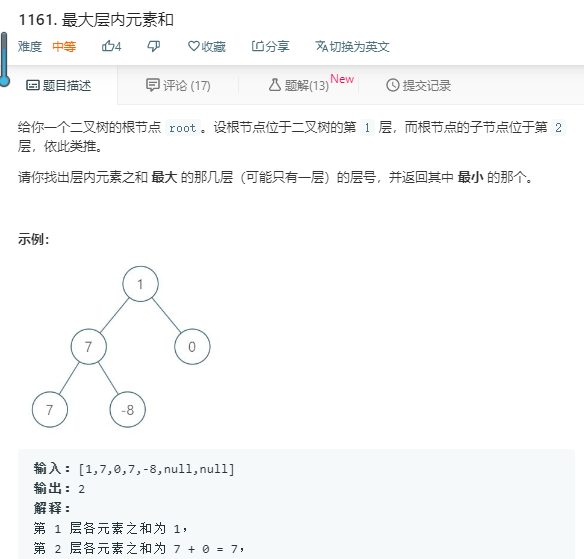
法1:
BFS

class Solution {
public:
int maxLevelSum(TreeNode* root) {
queue<TreeNode*> q;
q.push(root);
int maxv=root->val,res=1,layer=0;
while(!q.empty()){
layer++;
int n=q.size(),sum=0;
for(int i=0;i<n;i++){
TreeNode* tmp=q.front();q.pop();
sum+=tmp->val;
if(tmp->left) q.push(tmp->left);
if(tmp->right) q.push(tmp->right);
}
if(sum>maxv){
maxv=sum;
res=layer;
}
}
return res;
}
};
法2:
DFS:

借助map结构,遍历到各个层时,map[n] 就加上那个属于本层的节点的元素值。
class Solution {
public:
map<int,int> mp;
void dfs(TreeNode* root, int d){
if(!root){
return;
}
mp[d] += root->val;
dfs(root->left,d+1);
dfs(root->right,d+1);
}
int maxLevelSum(TreeNode* root) {
int res = 0, max_sum = INT_MIN;
dfs(root,1);
auto iter = mp.begin();
while(iter != mp.end()){
if(iter->second > max_sum){
max_sum = iter->second;
res = iter->first;
}
iter++;
}
return res;
}
};

解法1:
并查集
题目很拗口。。。但本质就是计算一个图的连通分量的个数,总石头数减去连通分量个数就是结果。
每次move移除掉一个共享同一行或列的(两个或多个石头)中的一个 如果把每个石头当一个点,如果两个石头间有共同x或y坐标,就给这两个点画一条线(边)。那么对应move操作就是把其中一条边的一个点删除,直到不能删为止,也就是说图里面的连通分量的点是要删去的,一直删到连通分量里面没有边(即只剩下一个点)
class Solution {
public:
vector<int> vec;
int removeStones(vector<vector<int>>& stones) {
int n = stones.size();
vec = vector<int>(n);
for(int i=0;i<n;++i){
vec[i] = i;
}
for(int i=0;i<n;++i){
for(int j=0;j<n;++j){
if(stones[i][0] == stones[j][0] || stones[i][1] == stones[j][1]){
Union(i,j);
}
}
}
int cnt=0;
for(int i=0;i<n;++i){
if(vec[i]==i){
cnt++;
}
}
return n - cnt;
}
int find(int i){
if(vec[i]!=i){
vec[i] = find(vec[i]);
}
return vec[i];
}
void Union(int x,int y){
int faA = find(x);
int faB = find(y);
vec[faA] = faB;
}
};
解法2:
DFS
DFS方法的解题思路: 用dfs求连通分量的个数 最后结果 = stones.size() - 连通分量的个数

class Solution {
public:
int removeStones(vector<vector<int>>& stones) {
vector<bool> vis(stones.size(),false);
int res = 0;
for(int i=0;i<stones.size();++i){
if(vis[i]==true){
continue;
}
dfs(stones,vis,i);
res++;
}
return stones.size()-res;
}
void dfs(vector<vector<int>>& stones,vector<bool>& vis,int k){
vis[k] = true;
int x = stones[k][0], y = stones[k][1];
for(int i=0;i<stones.size();++i){
if(vis[i]==true)
continue;
if(stones[i][0] == x || stones[i][1]==y){
dfs(stones,vis,i);
}
}
}
};

解法1:
并查集


class Solution {
public:
int find(vector<int>& union_find, int idx){
if(union_find[idx] == -1) return idx;
return find(union_find,union_find[idx]);
}
void Union(vector<int>&union_find, int idx1, int idx2){
int parent1 = find(union_find,idx1);
int parent2 = find(union_find,idx2);
//Always keep the same rule, merge parent1 to parent2;
if(parent1 != parent2) union_find[parent1] = parent2;
}
vector<vector<string>> accountsMerge(vector<vector<string>>& accounts) {
vector<vector<string>> res;
int n = accounts.size();
vector<int> union_find(n,-1);
map<string,int> mailUser;
map<int,vector<string>> mails;
for(int i=0; i<accounts.size(); i++){
for(int j=1; j<accounts[i].size(); j++){
if(mailUser.count(accounts[i][j])){
// if the same email has been stored before, find its user and unite them
int idx1 = find(union_find,i);
int idx2 = find(union_find,mailUser[accounts[i][j]]);
Union(union_find,idx1,idx2);
}
//**IMPORTANT**
//We can still assign this mail to the "current" user, because we have already performed union
mailUser[accounts[i][j]] = i;
}
}
for(auto pair:mailUser){
//Find its real user
int user = find(union_find,pair.second);
mails[user].push_back(pair.first);
}
for(auto pair:mails){
vector<string> temp = pair.second;
sort(temp.begin(),temp.end());
temp.insert(temp.begin(),accounts[pair.first][0]);
res.push_back(temp);
}
return res;
}
};

解法1:
DFS C++

class Solution {
private:
unordered_map<string,vector<pair<string,double>>> children;
pair<bool,double> search(string& a,string& b,unordered_set<string>& visited,double val){
if(visited.count(a) == 0){
visited.insert(a);
for(auto p : children[a]){
double temp = val * p.second;
if(p.first == b) return make_pair(true,temp);
auto result = search(p.first,b,visited,temp);
if(result.first){
return result;
}
}
}
return make_pair(false,-1.0);
}
public:
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
vector<double> ans;
for(int i = 0;i<equations.size();++i){
children[equations[i][0]].push_back(make_pair(equations[i][1],values[i]));
children[equations[i][1]].push_back(make_pair(equations[i][0],
1.0 / values[i]));
}
for(auto p : queries){
unordered_set<string> visited;
// p .first == p.second is special case
ans.push_back(p[0] == p[1] && children.count(p[0]) ?
1.0 : search(p[0],p[1],visited,1.0).second);
}
return ans;
}
};
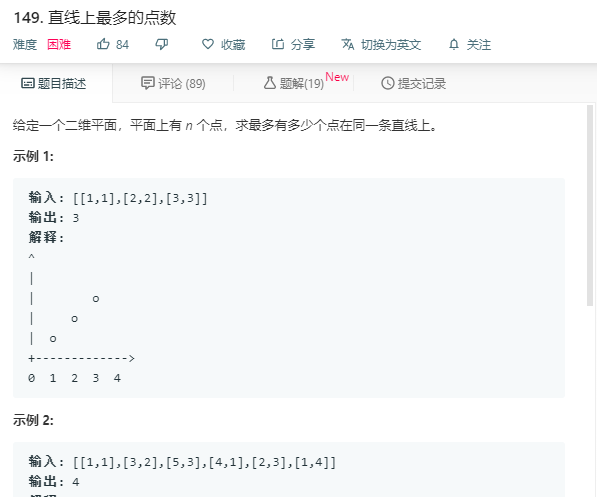

class Solution {
public:
int maxPoints(vector<vector<int>>& points) {
//两点确定一条直线
if(points.size()<3)return points.size();
int Max=0;
for(int i=0;i<points.size();++i)//i表示数组中的第i+1个点
{
//same用来表示和i一样的点
int same=1;
for(int j=i+1;j<points.size();++j)//j表示数组中的第j+1个点
{
int count=0;
// i、j在数组中是重复点,计数
if(points[i][0]==points[j][0]&&points[i][1]==points[j][1])same++;
else{//i和j不是重复点,则计算和直线ij在一条直线上的点
count++;
long long xDiff = (long long)(points[i][0] - points[j][0]);//Δx1
long long yDiff = (long long)(points[i][1] - points[j][1]);//Δy1
for (int k = j + 1; k < points.size(); k ++)//Δy1/Δx1=Δy2/Δx2 => Δx1*Δy2=Δy1*Δx2,计算和直线ji在一条直线上的点
if (xDiff * (points[i][1] - points[k][1]) == yDiff * (points[i][0] - points[k][0]))
count++;
}
Max=max(Max,same+count);
}
if(Max>points.size()/2)return Max;//若某次最大个数超过所有点的一半,则不可能存在其他直线通过更多的点
}
return Max;
}
};