Codeforces 776E: The Holmes Children （数论 欧拉函数）

题目链接

先看题目中给的函数f(n)和g(n)

　　对于f(n)，若自然数对(x,y)满足 x+y=n,且gcd(x,y)=1，则这样的数对对数为f(n)

证明f(n)=phi(n)

    设有命题 对任意自然数x满足x<n，gcd(x,n)=1等价于gcd(x,y)=1  成立，则该式显然成立，下面证明这个命题。
    
    假设gcd(x,y)=1时，gcd(x,n)=k!=1,则n=n'k,x=x'k,gcd(x,y)=gcd(x,n-x)=gcd(x'k,(n'-x')k)=k,与假设gcd(x,y)=1不符，故gcd(x,y)=1时，gcd(x,n)=1。同理可证gcd(x,n)=1时，gcd(x,y)=1。
    
    综上，f(n)=phi(n)

　　对于g(n),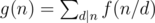，这个本人就不在博客里献丑了，推荐找本专门讲数论的书看下，估计都会有，这个可以当成是结论用，即 n的所有因数的欧拉函数之和等于n本身

解决了函数f(n)和g(n)的意义，剩下的就好解多了

时间上，由于连续进行两次n=phi(n)的运算至少可以将n减小为原来的一半，故肯定是不会T啦

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

//单独求解单个phi(x)
LL Eular(LL n)
{
    LL ret=n;
    for(LL i=2; i*i<= n; i++)
        if(n%i==0)
        {
            ret-=ret/i;
            while(n%i==0) n/= i;
        }
    if(n>1) ret-=ret/n;
    return ret;
}

LL n,k;

int main()
{
    while(cin>>n>>k)
    {
        k=(k+1)/2;
        while(k-- && n>1)
            n=Eular(n);
        cout<<n%1000000007<<endl;
    }
}