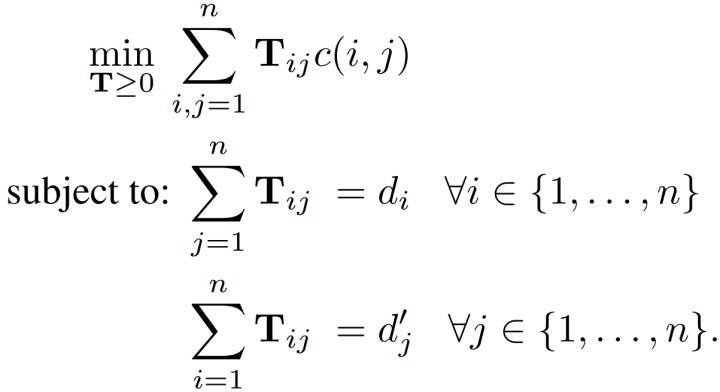机器学习是时下流行AI技术中一个很重要的方向,无论是有监督学习还是无监督学习都使用各种“度量”来得到不同样本数据的差异度或者不同样本数据的相似度。良好的“度量”可以显著提高算法的分类或预测的准确率,本文中将介绍机器学习中各种“度量”,“度量”主要由两种,分别为距离、相似度和相关系数,距离的研究主体一般是线性空间中点;而相似度研究主体是线性空间中向量;相关系数研究主体主要是分布数据。本文主要介绍其他度量。
1 KL散度——度量两个分布的距离
KL散度(Kullback–Leibler divergence)又称为相对熵(relative entropy)。KL散度是两个概率分布P和Q差别的非对称性的度量。 KL散度是用来 度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下,P表示数据的真实分布,Q表示数据的理论分布,模型分布,或P的近似分布。
对于离散随机变量,其概率分布P 和 Q的KL散度可按下式定义为
等价于
即按概率P求得的P和Q的对数商的平均值。KL散度仅当概率P和Q各自总和均为1,且对于任何i皆满Q(i)>0及P(i)>0时,才有定义。式中出现0ln 0的情况,其值按0处理。
对于连续随机变量,其概率分布P和Q可按积分方式定义为
其中p和q分别表示分布P和Q的密度。
更一般的,若P和Q为集合X的概率测度,且P关于Q绝对连续,则从P到Q的KL散度定义为
其中,假定右侧的表达形式存在,则dP/dP为Q关于P的R–N导数。
相应的,若P关于Q绝对连续,则
即为P关于Q的相对熵。
在这里举一个实际例子来说明KL散度如何计算的,假设P和Q是两个不同的分布。P是一个实验次数N=2且概率p为0.5 的二项分布。Q是一个各种取0,1或2的概率都为1/3的离散均匀分布。
| X | 0 | 1 | 2 |
|---|---|---|---|
| P(x) | 0.25 | 0.5 | 0.25 |
| Q(x) | 0.333 | 0.333 | 0.333 |
所以P关于Q的KL散度为
同理可得Q关于P的KL散度
2 词移距离——NLP领域计算文档相似度
在NLP领域中,Word2Vec得到的词向量可以反映词与词之间的语义差别,但在实际任务中我们经常遇到计算文档和文档之间相似度的问题,除了采用词向量叠加生成文章向量的方案,我们还有一个叫做词移距离(Word Mover's Distance)的方案来计算文档和文档之间的相似度。其中文档和文档之间距离定义为:
其中c(i,j)为i ,j两个词所对应的词向量的欧氏距离, Tij为词语xi转移到词语xj的权值。那我们怎样得到这个权值矩阵T呢?又或者说这个加权矩阵T代表什么含义呢?这个加权矩阵T有些类似于HMM中的状态转移矩阵,只不过其中的概率转换为权重了而已:
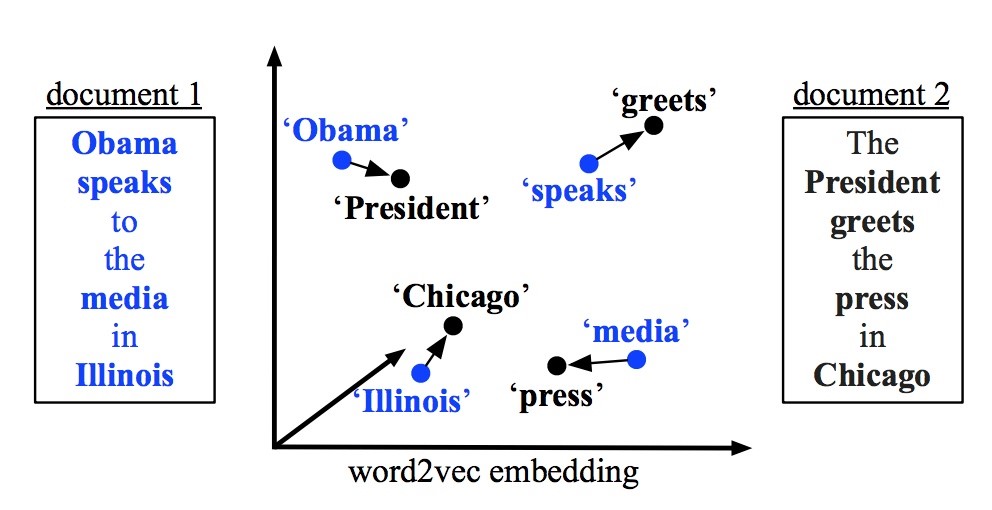
这里有两个文档1和文档2,去除停用词后,每篇文档仅剩下4个词。文档1文档的词语集合为{Obama, speaks, media, Illinois},文档2的词语集合为{President greets press Chicago}。我们就是要用这四个词来比较两个文档之间的相似度。在这里,我们假设’Obama’这个词在文档1中的的权重为0.5(可以简单地用词频或者TFIDF进行计算),那么由于’Obama’和’president’的相似度很高,那么我们可以给由’Obama’移动到’president’很高的权重,这里假设为0.4,文档2中其他的词由于和’Obama’的距离比较远,所以会分到更小的权重。这里的约束是,由文档1中的某个词i移动到文档2中的各个词的权重之和应该与文档1中的这个词i的权重相等,即’Obama’要把自己的权重0.5分给文档2中的各个词。同样,文档2中的某个词j所接受到由文档1中的各个词所流入的权重之和应该等于词j在文档2中的权重。为何要有这样的操作呢?因为词移距离代表的是文档1要转换为文档2所需要付出的总代价。将这种代价求得下界即最小化之后,即可求得所有文档a中单词转移到文档b中单词的最短总距离,代表两个文档之间的相似度。当然实际计算中权值矩阵T也不是随便而来的,词移距离对应一个优化我呢提,它是这样计算的: