隐马模型是一个不复杂但在NLP上最有效、快速的方法。
1.通信模型
自然语言和通信的联系是天然的,当自然语言处理问题回归到通信系统中的解码问题时,很多难题就迎刃而解了。
前面已经说了,我们把说话看作是一种编码方式,然后通过喉咙、空气传播,听到话的人的耳朵接收,再理解说的话,也就是语音识别。如果接收端是计算机,那么计算机完成的就是语音识别。我们要根据接收端的信号O1,O2,O3...来推测发送源的信号S1,S2....。我们只需从所有的源信息中找到最有可能的信号即可,也就是:
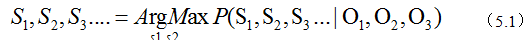
上式不易直接求出,我们利用贝叶斯公式等价成:
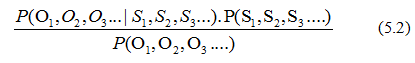 、
、
一旦信息产生,接收端收到的信息就不会改变了,所以我们可以把分母当成一个常数,只考虑分子,分子有两项,我们采用隐马尔可夫模型来估计。
2.隐马尔可夫模型
上面我们提到过,马尔科夫假设是指随机过程中的各个状态St的概率分布只与它的前一个状态St-1有关。
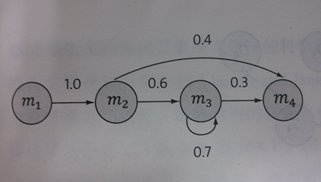
如上图,四个圈表示四个状态,每条变表示一个可能的状态转换,边上的权值是转移概率。例如m2到m3的可能性为0.6,到m4的可能性为0.4,即:
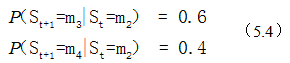
此处的概率,我们可以运行一段时间之后,通过观察得到。
而我们这里要讲的隐马尔可夫模型,其实是上述马尔可夫链的扩展,它表示:在任一时刻t的状态St是不可见的。但是隐马模型在每个时刻t会输出一个符号Ot,且Ot和St相关且仅和St相关。
基于马尔科夫假设和独立输出假设,我们可以计算出某个特定的状态序列S1,S2,S3...产生输出符号O1,O2,O3...的概率。

带入(5.2)中的分母。这样通信的解码问题就可以用隐马尔可夫模型解决了。因为通信和自然语言处理的相似性,我们可以用隐马尔可夫模型来解决。至于如何找出上式的最大值,进而识别原始句子S,则需要维特比算法(后面会有介绍)。
3.延伸阅读:隐含马尔科夫模型的训练
围绕隐马模型有三个基本问题:
1.给定模型,如何计算某个特定输出序列的概率;——解决:用Forward-Backward算法
2.给定一个模型和某个特定的输出序列,如何找到最可能产生的输出序列;——解决:维特比算法
3.给定足够靓的观测数据,如何估计隐马模型的参数。
此处,我们讨论第三个问题。
隐马尔可夫模型的参数有两类,一类是转移概率,即从一个状态转移到另一个状态的概率P(St|St-1),比如前面从m3到m2的概率;另一类是生成概率,即每个状态St产生相应输出符号Ot的概率P(Ot|St)。我们的目的就是要训练出这些参数。
在监督训练中,我们用足够的数据,进行频率估计得到参数。但是很多应用中不可能做到,或者成本非常高。因此,训练隐马尔可夫模型更使用的方式是通过大量观测信号O1,O2,O3....就能推算参数,常用的方法是鲍姆-韦尔奇算法。
一般来说,根据观察值倒推产生它的隐马模型可能会有多个值。但总有一个的可能性要比其他高。鲍姆-韦尔奇算法就是寻找这个最有可能的模型。
基本思想如下:找到一组能产生输出序列O的模型。然后在此基础上找到更好的模型。以此不断迭代知道模型质量没有明显提高为止。迭代使用EM估计,只能找到局部最优。
4.小结
隐马尔可夫模型最初应用于通信领域,继而推广到语音和语言处理中。它需要一个训练算法(鲍姆-韦尔奇算法)和使用时的解码算法(维特比算法),掌握了它们,就基本上可以使用隐马尔可夫模型了。