zoukankan html css js c++ java

好困啊

P1120 小木棍［数据加强版］

题目描述

乔治有一些同样长的小木棍，他把这些木棍随意砍成几段，直到每段的长都不超过

现在，他想把小木棍拼接成原来的样子，但是却忘记了自己开始时有多少根木棍和它们的长度。

给出每段小木棍的长度，编程帮他找出原始木棍的最小可能长度。

输入输出格式

输入格式：

共二行。

第一行为一个单独的整数N表示砍过以后的小木棍的总数，其中

（管理员注：要把超过

第二行为

输出格式：

一个数，表示要求的原始木棍的最小可能长度

输入输出样例

输入样例#1：复制

9
5 2 1 5 2 1 5 2 1

输出样例#1：复制

说明

2017/08/05

数据时限修改：

-#17 #20 #22 #27 四组数据时限

-#21 #24 #28 #29 #30五组数据时限

其他时限改为

/*
dfs好难啊 
这个状态就想不到 
*/
#include <bits/stdc++.h>

#define N 100007

using namespace std;
int num[N];
int maxn,minn,sum,k,m,n,temp;

inline int read()
{
    int x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

void dfs(int cnt,int already,int need,int can) 
{                                                 
    if(cnt==0){printf("%d",need); exit(0);}
    if(already==need) 
    {
        dfs(cnt-1,0,need,maxn);
        return ;
    }
    for(int i=can; i>=minn; i--)
        if(num[i] && i+already<=need)
        {
            num[i]--;dfs(cnt,already+i,need,i);
            num[i]++;
            if(already==0 || already+i==need) return ;
        }
}

int main()
{
    n=read();
    for(int i=1; i<=n; i++)
    {
        k=read();
        if(k<=50)       
        {
            sum+=k;num[k]++;
            minn=min(k,minn);
            maxn=max(k,maxn);
        }
    }
    temp=sum/2;
    for(int i=maxn;i<=temp;i++)  
    if(sum%i==0) dfs(sum/i,0,i,maxn);
    printf("%d",sum);
    return 0;
}

P1118 [USACO06FEB]数字三角形

题目描述

FJ and his cows enjoy playing a mental game. They write down the numbers from

    3   1   2   4
      4   3   6
        7   9
         16

Behind FJ's back, the cows have started playing a more difficult game, in which they try to determine the starting sequence from only the final total and the number

Write a program to help FJ play the game and keep up with the cows.

有这么一个游戏：

写出一个 $11至NN的排列a_iai，然后每次将相邻两个数相加，构成新的序列，再对新序列进行这样的操作，显然每次构成的序列都比上一次的序列长度少11，直到只剩下一个数字位置。下面是一个例子：$

最后得到

现在想要倒着玩这样一个游戏，如果知道 $NN，知道最后得到的数字的大小sumsum，请你求出最初序列a_iai，为11至NN的一个排列。若答案有多种可能，则输出字典序最小的那一个。$

[color=red]管理员注：本题描述有误，这里字典序指的是

而不是

输入输出格式

输入格式：

两个正整数

输出格式：

输出包括

当无解的时候，请什么也不输出。（好奇葩啊）

输入输出样例

输入样例#1：复制

4 16

输出样例#1：复制

3 1 2 4

说明

对于 $40\%40%的数据，n≤7n≤7；$

对于 $80\%80%的数据，n≤10n≤10；$

对于 $100\%100%的数据，n≤12,sum≤12345n≤12,sum≤12345。$

#include<bits/stdc++.h>

#define N 77777

using namespace std;
int n,m,ans,cnt;
int a[N],tmp[N],sum[N];
int vis[N];

bool judge()
{
//    if(a[1]==n) exit(0); 加上这句剪枝蜜汁WA一个点 
    for(int i=1;i<=n;i++) tmp[i]=a[i];
    cnt=n;
    while(cnt)
    {
        for(int i=1;i<=cnt;i++)
          sum[i]=tmp[i]+tmp[i+1];
        for(int i=1;i<=cnt-1;i++) tmp[i]=sum[i];
        tmp[cnt]=0;cnt--;
    }
    if(sum[1]==m) return true;
    else return false;
}

void dfs(int k)
{
    if(k==n+1)
    {
        if(judge()) 
        {
            for(int i=1;i<=n;i++)
              printf("%d ",a[i]);
            exit(0);
        } 
        return;
    } 
    for(int i=1;i<=n;i++)
    {
        if(vis[i]) continue;
        a[k]=i;vis[i]=1;dfs(k+1);
        vis[i]=0;
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    dfs(1);
    return 0;
}

60暴力

/*
如果n为4，那么sum是a+3b+3c+d。
如果n为5,那么sum是a+4b+6c+4d+e。
如果n为6，那么sum是a+5b+10c+10d+5e+f
系数 杨辉三角
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
int f[130][130]={0};
int a[130]={0};
bool v[130]={true};
int n=0,m,sum=0;

void init()
{
    scanf("%d%d",&n,&sum);
    for (int i=1;i<=n;i++) f[i][1]=1;
    for (int i=2;i<=n;i++) for (int j=2;j<=i;j++)
    f[i][j]=f[i-1][j]+f[i-1][j-1];
    m=0;
    memset(v,true,sizeof(v));
}

void dfs(int i)
{
    if (m>sum) return;
    if (i==n+1)
    {
        if (sum==m)
        {
            for (int j=1;j<=n;j++)
              printf("%d ",a[j]);
            exit(0);
        }
        return;
    }
    for (int j=1;j<=n;j++)
      if (v[j])
        {
            a[i]=j;m+=f[n][i]*j;
            v[j]=false;dfs(i+1);
            a[i]=0;m-=f[n][i]*j;
            v[j]=true;
        }
}

main()
{
    init();
    dfs(1);
    return 0;
}

P2123 皇后游戏

题目背景

还记得 NOIP 2012 提高组 Day1 的国王游戏吗？时光飞逝，光阴荏苒，两年

过去了。国王游戏早已过时，如今已被皇后游戏取代，请你来解决类似于国王游

戏的另一个问题。

题目描述

皇后有 n 位大臣，每位大臣的左右手上面分别写上了一个正整数。恰逢国庆

节来临，皇后决定为 n 位大臣颁发奖金，其中第 i 位大臣所获得的奖金数目为第

i－1 位大臣所获得奖金数目与前 i 位大臣左手上的数的和的较大值再加上第 i 位

大臣右手上的数。

形式化地讲：我们设第 i 位大臣左手上的正整数为 ai，右手上的正整数为 bi，

则第 i 位大臣获得的奖金数目为 ci可以表达为：

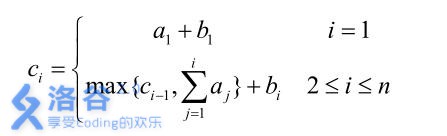
当然，吝啬的皇后并不希望太多的奖金被发给大臣，所以她想请你来重新安

排一下队伍的顺序，使得获得奖金最多的大臣，所获奖金数目尽可能的少。

注意：重新安排队伍并不意味着一定要打乱顺序，我们允许不改变任何一

位大臣的位置。

输入输出格式

输入格式：

第一行包含一个正整数 T，表示测试数据的组数。

接下来 T 个部分，每个部分的第一行包含一个正整数 n，表示大臣的数目。

每个部分接下来 n 行中，每行两个正整数，分别为 ai和 bi，含义如上文所述。

输出格式：

共 T 行，每行包含一个整数，表示获得奖金最多的大臣所获得的奖金数目。

输入输出样例

输入样例#1：复制

输出样例#1：复制

输入样例#2：复制

输出样例#2：复制

528
902

说明

按照 1、2、3 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 10；

按照 1、3、2 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 9；

按照 2、1、3 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 9；

按照 2、3、1 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 8；

按照 3、1、2 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 9；

按照 3、2、1 这样排列队伍，获得最多奖金的大臣获得奖金的数目为 8。

当按照 3、2、1 这样排列队伍时，三位大臣左右手的数分别为：

(1, 2)、(2, 2)、(4, 1)

第 1 位大臣获得的奖金为 1 + 2 = 3；

第 2 位大臣获得的奖金为 max{3, 3} + 2 = 5；

第 3 为大臣获得的奖金为 max{5, 7} + 1 = 8。

对于全部测试数据满足： $a_i, b_i le 10^91≤ai,bi≤109。$

/*
https://www.luogu.org/blog/namasikanam/solution-p2123
*/
#include <iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

#define ll long long
#define N 50007

using namespace std;
struct node
{
    int a,b,d;
} D[N];

inline bool cmp(const node &x, const node &y)
{
    if (x.d != y.d)
        return x.d < y.d;
    if (x.d <= 0)
        return x.a < y.a;
    else
        return x.b > y.b;
}

inline int read()
{
    int x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

int main()
{
    int T;
    T=read();
    while (T--)
    {
        int n;
        memset(D,0,sizeof D);
        n=read();
        for (int i = 1; i <= n; ++i)
        {
            D[i].a=read();D[i].b=read();
            D[i].d = D[i].a - D[i].b;
            if (D[i].d) D[i].d /= abs(D[i].d);
        }
        sort(D + 1, D + n + 1, cmp);
        ll c = 0, s = 0;a
        for (int i = 1; i <= n; ++i)
        {
            s+=D[i].a;
            c=max(c, s) + D[i].b;
        }
        printf("%lld
", c);
    }
}

贪心神题

P1441 砝码称重

题目描述

现有n个砝码，重量分别为a1，a2，a3，……，an，在去掉m个砝码后，问最多能称量出多少不同的重量（不包括0）。

输入输出格式

输入格式：

输入文件weight.in的第1行为有两个整数n和m，用空格分隔

第2行有n个正整数a1，a2，a3，……，an，表示每个砝码的重量。

输出格式：

输出文件weight.out仅包括1个整数，为最多能称量出的重量数量。

输入输出样例

输入样例#1：复制

3 1
1 2 2

输出样例#1：复制

说明

【样例说明】

在去掉一个重量为2的砝码后，能称量出1，2，3共3种重量。

【数据规模】

对于20%的数据，m=0；

对于50%的数据，m≤1；

对于50%的数据，n≤10；

对于100%的数据，n≤20，m≤4，m＜n，ai≤100。

#include<bits/stdc++.h>

#define N 2007

using namespace std;
int n,m,ans,cnt,tot;
int can[N],vis[N],use[N],w[N];

void dfs(int k,int sum)
{
    if(k==n)
    {
        tot=0;
        for(int i=1;i<=N;i++) if(vis[i]) tot++;
        ans=max(ans,tot);
        return;
    }
    for(int i=k+1;i<=n;i++)
    {
        if(can[i]==2) continue;
        vis[sum+w[i]]=1;can[i]=1;
        dfs(i,sum+w[i]);
        if(can[i]==1) can[i]=0;
    }
}

void pre(int k)
{
    if(k==m+1)
    {
        memset(vis,0,sizeof vis);
        dfs(0,0);
        return;
    }
    for(int i=1;i<=n;i++)
    {
        if(use[i]) continue;
        use[i]=1;can[i]=2;pre(k+1);
        use[i]=0;can[i]=0;
    }
}
 
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    pre(1);
    printf("%d
",ans);
    return 0;
}

50暴力

/*
dfs预处理状态
dp更新答案 f[i]是i能凑出来，就成了01背包。 
如果用f[i]表示1~i的数量，那么转移时许多情况特别难处理。 
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 2001

using namespace std;
int n,m,last,num,ans;
int a[N],f[N],b[N]; 

void dfs(int k)
{
    if(k==m+1)
    {
        memset(f,0,sizeof(f));f[0]=1;
        for(int i=1;i<=n;i++)
        {
            if(b[i]==0)
            {
                for(int j=2000-a[i];j>=0;j--)
                if(f[j]!=0) f[j+a[i]]=1;
            }
        }
        num=0;
        for(int i=1;i<=2000;i++) if(f[i]) num++;
        ans=max(ans,num);
        return;
    }
    for(int i=last+1;i<=n;i++)
    {
        b[i]=1;last=i;
        dfs(k+1);b[i]=0;
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    dfs(1);
    printf("%d
",ans);
    return 0;
}

View Code

御坂网络

链接：https://www.nowcoder.com/acm/contest/212/A
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 131072K，其他语言262144K
64bit IO Format: %lld

题目描述

作为「Misaka Network」的中心司令塔的 LastOrder出事了，为了维持「Misaka Network」的正常工作，需要临时选出一个Sister作为中心司令塔。

为了弥补能力上的不足，对于选出的Sister有一些要求。
具体来说，平面上有 n 个 Sister，问能否找到一个Sister作为中心司令塔，使得其他 Sister 都在以她为圆心的一个圆上，如果找不到这样的Sister，则输出 "-1"(不含引号)。

输入描述:

第一行一个数 n
接下来 n 行，第 i 行两个整数 x

, y

 ，表示第 i 个Sister在平面上的坐标。

输出描述:

输出共一个数，表示选出的Sister的编号，如果找不到则输出 "-1"。

示例1

输入

复制

输出

复制

备注:

3 ≤ n ≤ 1000,-10

⁹

≤ x

, y

 ≤ 10

⁹

 ，所有坐标互不相同。

/*
不明白为什么用pow不对
*/
#include <bits/stdc++.h>
 
#define LL long long
#define MAXN 1007
 
using namespace std;
struct Node
{
    LL x, y;
}a[MAXN];
int main()
{
    ios::sync_with_stdio(false); cout.tie(0); cin.tie(0);
    int n; cin>>n;
    for(int i=1; i<=n; i++) cin>>a[i].x>>a[i].y;
    int ok = 0, ind;
    for(int i=1; i<=n; i++)
    {
        LL d;
        if(i==1) d=(a[2].x-a[1].x)*(a[2].x-a[1].x)+(a[2].y-a[1].y)*(a[2].y-a[1].y);
        else d=(a[i].x-a[1].x)*(a[i].x-a[1].x)+(a[i].y-a[1].y)*(a[i].y-a[1].y);
        int yes = 0;
        for(int j=1; j<=n; j++)
        {
            if(i==j) continue;
            LL t = (a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y);
            if(t != d)
            {
                yes = 1;
                break;
            }
        }
        if(!yes)
        {
            ok = 1;
            ind = i;
            break;
        }
    }
    if(ok) cout<<ind<<endl;
    else cout<<-1<<endl;
    return 0;
}

View Code

------——————————————————————————————————————————————————————————————————————————————————

P3952 时间复杂度

题目描述

小明正在学习一种新的编程语言 A++，刚学会循环语句的他激动地写了好多程序并给出了他自己算出的时间复杂度，可他的编程老师实在不想一个一个检查小明的程序，于是你的机会来啦！下面请你编写程序来判断小明对他的每个程序给出的时间复杂度是否正确。

A++语言的循环结构如下：

F i x y
    循环体
E

其中F i x y表示新建变量

“E”表示循环体结束。循环体结束时，这个循环体新建的变量也被销毁。

注：本题中为了书写方便，在描述复杂度时，使用大写英文字母“O”表示通常意义下“Θ”的概念。

输入输出格式

输入格式：

输入文件第一行一个正整数

接下来每个程序的第一行包含一个正整数 $串表示这个程序的复杂度，O(1)表示常数复杂度，O(n^w)表示复杂度为n^wnw，其中w是一个小于100的正整数（输入中不包含引号），输入保证复杂度只有O(1)和O(n^w) 两种类型。$

接下来

程序行若以E开头，则表示循环体结束。

输出格式：

输出文件共

注意：即使在程序不会执行的循环体中出现了语法错误也会编译错误，要输出 ERR。

输入输出样例

输入样例#1：复制

8
2 O(1)
F i 1 1
E
2 O(n^1)
F x 1 n
E
1 O(1)
F x 1 n
4 O(n^2)
F x 5 n
F y 10 n
E
E
4 O(n^2)
F x 9 n
E
F y 2 n
E
4 O(n^1)
F x 9 n
F y n 4
E
E
4 O(1)
F y n 4
F x 9 n
E
E
4 O(n^2)
F x 1 n
F x 1 10
E
E

输出样例#1：复制

Yes
Yes
ERR
Yes
No
Yes
Yes
ERR

说明

【输入输出样例解释1】

第一个程序

第二个程序

第三个程序有一个 F 开启循环却没有 E 结束，语法错误。

第四个程序二重循环，

第五个程序两个一重循环，

第六个程序第一重循环正常，但第二重循环开始即终止（因为

第七个程序第一重循环无法进入，故为常数复杂度。

第八个程序第二重循环中的变量

【数据规模与约定】

对于 $30\%30%的数据：不存在语法错误，数据保证小明给出的每个程序的前 L/2L/2 行一定为以 F 开头的语句，第 L/2+1L/2+1 行至第 LL 行一定为以 EE 开头的语句，L le 10L≤10，若 xx、yy 均为整数，xx 一定小于 yy，且只有 yy 有可能为 nn。$

对于 $50\%50%的数据：不存在语法错误，L le 100L≤100，且若 xx、yy 均为整数，xx 一定小于 yy，且只有 yy 有可能为 nn。$

对于 $70\%70%的数据：不存在语法错误，L le 100L≤100。$

对于 $100\%100%的数据：L le 100L≤100。$

/*
s_tack[]:是否匹配
sta[]:编号 
vis[]:变量名重复
g[]:对复杂度有贡献 
tmp:累乘复杂度 
*/
#include<bits/stdc++.h>

#define N 107

using namespace std;
int n,m,tmp,ans,top,Top;
int cur,flag,flag1,opt;
int sta[N],g[N];
char O[6],s_tack[N<<1],a,b,c,d;
char s[N][5];
map<char,bool>vis;
string e,f;

inline int read()
{
    int x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

void clear() 
{
    top=0;flag=0;tmp=0;ans=0;flag1=0;
    cur=0;Top=0;
    memset(g,0,sizeof g);
    memset(sta,0,sizeof sta);
    memset(O,0,sizeof O);
    memset(s_tack,0,sizeof s_tack);
}

bool compair(string aa,string bb)//错误1 比较函数写错 
{
    if(aa.length()<bb.length()) return false;
    if(aa.length()>bb.length()) return true;
    for(int i=0;i<aa.length();i++)
    {
        if(aa[i]-'0'<bb[i]-'0') return false;
        if(aa[i]-'0'>bb[i]-'0') return true;
    }return false;
}

int main()
{
    int T;T=read();
    while(T--)
    {
        clear();
        n=read();
        scanf("%s",O);
        int l=strlen(O);
        opt=0;
        if(l==6) opt=O[4]-'0';
        if(l==7) opt=(O[4]-'0')*10+O[5]-'0';
        if(l==8) opt=(O[4]-'0')*100+(O[5]-'0')*10+O[6]-'0';
        //错误2 没考虑到O(n^m) m>10的情况，直接把m当做O[4] 
        for(int i=1;i<=n;i++)
        {
            cin>>a;
            if(a=='F')cin>>b>>e>>f;//错误3：string的读入 
            if(e[0]=='n' && f[0]!='n') flag1=1;//错误4:没考虑"n n"的情况 
            if(compair(e,f) && f[0]!='n') flag1=1,g[i]=2;
            if(e.length()==1) c=e[0];
            else c='1';
            if(f.length()==1) d=f[0];
            else d='1';
             s[i][0]=a;s[i][1]=b;s[i][2]=c;s[i][3]=d;//错误5：没考虑数字可能大于10的情况 
             
            if(!top && s[i][0]=='F') 
            {
                top+=1;s_tack[top]='F';Top+=1;sta[Top]=i;
                if(vis[s[i][1]]) {flag=1;continue;}//错误6：continue写成break，导致输入不完。 
                vis[s[i][1]]=1;
                if((s[i][2]!='n'&&s[i][3]!='n') || s[i][2]==s[i][3] || s[i][2]=='n' ||flag1) continue;
                else tmp+=1,g[i]=1;ans=max(ans,tmp);//错误7 忘记s[i][2]<s[i][3]的情况 
                continue;
            }
            if(!top && s[i][0]=='E') {flag=1;continue;}
            
            if(top)
            {
                if(s[i][0]=='F')
                {
                    top+=1;s_tack[top]='F';Top+=1;sta[Top]=i; 
                    if(vis[s[i][1]]){flag=1;continue;}
                    vis[s[i][1]]=1;
                    if((s[i][2]!='n'&&s[i][3]!='n') || s[i][2]==s[i][3] || s[i][2]=='n') continue;
                    else if(flag1) continue;
                    else tmp+=1;g[i]=1;ans=max(ans,tmp);
                }
                if(s[i][0]=='E')
                {
                    top-=1;int pos=sta[Top];
                    vis[s[pos][1]]=0;Top-=1;
                    if(flag1 && g[pos]==2) flag1=0;
                    if(g[pos]==1) tmp-=1;
                }
            }
        }
        
        if(flag || top)//错误9 没考虑少E的情况 
        {
            while(top)
            {
                top--;int pos=sta[Top];
                vis[s[pos][1]]=0;Top--;
            }
            printf("ERR
");
        }
        else if((opt==0&&!ans) || opt==ans) printf("Yes
");
        else printf("No
");
    }
}

View Code

P3953 逛公园

题目描述

策策同学特别喜欢逛公园。公园可以看成一张

策策每天都会去逛公园，他总是从1号点进去，从

策策喜欢新鲜的事物，它不希望有两天逛公园的路线完全一样，同时策策还是一个特别热爱学习的好孩子，它不希望每天在逛公园这件事上花费太多的时间。如果1号点到

策策同学想知道总共有多少条满足条件的路线，你能帮帮它吗？

为避免输出过大，答案对

如果有无穷多条合法的路线，请输出

输入输出格式

输入格式：

第一行包含一个整数

接下来

接下来 $MM行，每行三个整数a_i,b_i,c_iai,bi,ci，代表编号为a_i,b_iai,bi的点之间有一条权值为 c_ici的有向边，每两个整数之间用一个空格隔开。$

输出格式：

输出文件包含

输入输出样例

输入样例#1：复制

输出样例#1：复制

3
-1

说明

【样例解释1】

对于第一组数据，最短路为

【测试数据与约定】

对于不同的测试点，我们约定各种参数的规模不会超过如下

测试点编号					是否有0边
1	5	5	10	0	否
2	5	1000	2000	0	否
3	5	1000	2000	50	否
4	5	1000	2000	50	否
5	5	1000	2000	50	否
6	5	1000	2000	50	是
7	5	100000	200000	0	否
8	3	100000	200000	50	否
9	3	100000	200000	50	是
10	3	100000	200000	50	是

对于 100%的数据, $10^9,1 le a_i,b_i le N ,0 le c_i le 10001≤P≤109,1≤ai,bi≤N,0≤ci≤1000。$

数据保证：至少存在一条合法的路线。

#include<bits/stdc++.h>

#define b 1000007
#define ll long long

using namespace std;
ll n,m,k,p,ans,cnt;
ll head[b],dis[b],C[b];
ll vis[b];
struct edge{
    ll u,v,net,w;
}e[b<<1];
queue<ll>q;

inline void add(int u,int v,int w)
{
    e[++cnt].v=v;e[cnt].w=w;e[cnt].net=head[u];head[u]=cnt;
}

inline ll read()
{
    ll x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

void spfa(int u)
{
    dis[u]=0;vis[u]=1;C[u]=1;q.push(u);
    while(!q.empty())
    {
        int now=q.front();q.pop();
        vis[now]=0;
        for(int i=head[now];i;i=e[i].net)
        {
            int v=e[i].v;
            if(dis[v]>dis[now]+e[i].w)
            {
                dis[v]=dis[now]+e[i].w;
                C[v]=C[u];
                if(!vis[v]) vis[v]=1,q.push(v);
            }
            else if(dis[v]==dis[now]+e[i].w) 
            {
                if(!vis[v]) vis[v]=1,q.push(v);
                C[v]+=C[u];C[v]%=p;
            }
        }
    }
}

void clear()
{
    memset(C,0,sizeof C);
    memset(dis,127/3,sizeof dis);
    memset(vis,0,sizeof vis);
    memset(head,0,sizeof head);
    memset(e,0,sizeof e);
    while(!q.empty()) q.pop();
    cnt=0;
}

int main()
{
    int T;T=read();
    while(T--)
    {
        clear();
        n=read();m=read();k=read();p=read();
        int x,y,z;
        for(int i=1;i<=m;i++)
        {
            x=read();y=read();z=read();
            add(x,y,z);
        }
        spfa(1);C[n]%=p;
        cout<<C[n]<<endl;
    }
}

20暴力

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<queue>

#define N 200007

using namespace std;
int T,b,n,m,k,mod,cnt,head[N];
int from[N],to[N],w[N];
int dis[N],vis[N],dp[N][51];
int in[N],re[N],flag;
struct edge{
    int next,to,w;
}e[N<<1];
queue<int>q;

inline int read()
{
    int x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

void add(int x,int y,int w)
{
    e[++cnt]=(edge){head[x],y,w};
    head[x]=cnt;
}

int DFS(int x,int res)//返回到达x点还剩res步可以绕的方案数
{
    if(~dp[x][res]) return dp[x][res];
    dp[x][res]=(x==1);
    for(int i=head[x];i;i=e[i].next)
    {
        int R=e[i].to;
        int tt=res-((dis[R]+e[i].w)-dis[x]);//通过这条边多绕了一会
        if(tt<0) continue;
        if(in[R]&&re[R]==tt) flag=1;//如果说res一直没有减少的情况下搜出来一个圈，说明有0环
        else in[R]=1,re[R]=tt;
        (dp[x][res]+=DFS(R,tt))%=mod;
        in[R]=0;re[R]=0;
    }
    return dp[x][res];
}
void Work()
{
    memset(head,0,sizeof(head));cnt=0;
    b=read();m=read();k=read();mod=read();
    for(int i=1;i<=m;i++)
    {
        from[i]=read();to[i]=read();w[i]=read();
        add(from[i],to[i],w[i]);
    }
    
    memset(dis,63,sizeof(dis));
    q.push(1);dis[1]=0;vis[1]=1;
    while(!q.empty())
    {
        int x=q.front();
        for(int i=head[x];i;i=e[i].next)
        {
            int R=e[i].to;
            if(dis[R]<=dis[x]+e[i].w) continue;
            dis[R]=dis[x]+e[i].w;
            if(!vis[R]) vis[R]=1,q.push(R);
        }
        q.pop();vis[x]=0;
    }

    memset(head,0,sizeof(head));cnt=0;
    memset(dp,-1,sizeof(dp));flag=0;
    for(int i=1;i<=m;i++)
        add(to[i],from[i],w[i]);
    DFS(b,k);
    printf("%d
",flag?-1:DFS(b,k));
}
int main()
{
    T=read();
    while(T--)Work();  
    return 0;
}

View Code

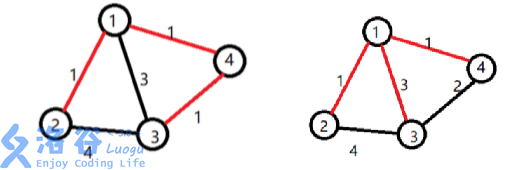
P3959 宝藏

题目描述

参与考古挖掘的小明得到了一份藏宝图，藏宝图上标出了

小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是，每个宝藏屋距离地面都很远，也就是说，从地面打通一条到某个宝藏屋的道路是很困难的，而开发宝藏屋之间的道路则相对容易很多。

小明的决心感动了考古挖掘的赞助商，赞助商决定免费赞助他打通一条从地面到某个宝藏屋的通道，通往哪个宝藏屋则由小明来决定。

在此基础上，小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以任意通行不消耗代价。每开凿出一条新道路，小明就会与考古队一起挖掘出由该条道路所能到达的宝藏屋的宝藏。另外，小明不想开发无用道路，即两个已经被挖掘过的宝藏屋之间的道路无需再开发。

新开发一条道路的代价是：

L代表这条道路的长度，K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的宝藏屋的数量（包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋）。

请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路，使得工程总代价最小，并输出这个最小值。

输入输出格式

输入格式：

第一行两个用空格分离的正整数

接下来

输出格式：

一个正整数，表示最小的总代价。

输入输出样例

输入样例#1：复制

输出样例#1：复制

输入样例#2：复制

输出样例#2：复制

说明

#include<bits/stdc++.h>

#define N 10001
#define inf 0x3f3f3f3f
#define ll long long

using namespace std;
ll n,m,k,ans,cnt,res,cur;
ll head[N],vis[N],can[N];
struct edge{
    ll u,v,net,w;
}e[N<<1];

inline ll read()
{
    ll x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

inline void add(int u,int v,int w)
{
    e[++cnt].v=v;e[cnt].w=w;e[cnt].net=head[u];head[u]=cnt;
}

void dfs(int now,ll val,ll tot,ll deep)
{
    if(val>=ans) return;
    if(tot==n)
    {
        ans=min(ans,val);
        return;
    }
    for(int i=head[now];i;i=e[i].net)
    {
        int v=e[i].v;
        if(!vis[v])
        {
            vis[v]=1;
            dfs(v,val+e[i].w*deep,tot+1,deep+1);        
            dfs(now,val+e[i].w*deep,tot+1,deep);
            dfs(cur,val+e[i].w*deep,tot+1,1);
            vis[v]=0;    
        }
    }
}

int main()
{
    int x,y,z;
    n=read();m=read();
    for(int i=1;i<=m;i++)
    {
        x=read();y=read();z=read();
        add(x,y,z);add(y,x,z);
    }ans=inf;
    for(int i=1;i<=n;i++)
    {
        memset(vis,0,sizeof vis);cur=i;
        vis[i]=1;dfs(i,0,1,1);
    }
    printf("%lld
",ans);
    return 0;
}

60暴力

折花枝，恨花枝，准拟花开人共卮，开时人去时。怕相思，已相思，轮到相思没处辞，眉间露一丝。

查看全文

相关阅读:
生成对抗性网络GAN
一些程序员好用的网站
 TED演讲积累。
JQuery$.extend()用法
 jQuery中判断数组
 input标签中的accpet
gitlab的添加密钥
 Linux—Ubuntu14.0.5 修改gitlab管理员的密码
 Linux—Ubuntu14.0.5安装gitlab
Linux—Ubuntu14.0.5安装Redis

原文地址：https://www.cnblogs.com/L-Memory/p/9781633.html

好困啊

P1120 小木棍 ［数据加强版］

题目描述

输入输出格式

输入输出样例

说明

P1118 [USACO06FEB]数字三角形

题目描述

输入输出格式

输入输出样例

说明

P2123 皇后游戏

题目背景

题目描述

输入输出格式

输入输出样例

说明

P1441 砝码称重

题目描述

输入输出格式

输入输出样例

说明

题目描述

输入描述:

输出描述:

输入

输出

备注:

P3952 时间复杂度

题目描述

输入输出格式

输入输出样例

说明

P3953 逛公园

题目描述

输入输出格式

输入输出样例

说明

P3959 宝藏

题目描述

输入输出格式

输入输出样例

说明

P1120 小木棍［数据加强版］