感觉自己以前的blog又长又乱,打算把几个多项式算法分开,就有了这几篇更乱的文章
其他多项式算法传送门:
[多项式算法](Part 2)NTT 快速数论变换 学习笔记
[多项式算法](Part 3)MTT 任意模数FFT/NTT 学习笔记
[多项式算法](Part 4)FWT 快速沃尔什变换 学习笔记
(Easy-1.FFT)
定义
-
FFT((Fast Fourier Transformation))
中文名称:快速傅里叶离散变换
(Fake Funny TLE)
(Q:)这个东西是用来干什么的呢?
(A:)想必大家都知道(FFT)可以快速求高精乘法吧。
利用(FFT)可以做到在(O(nlog_2n))的复杂度内快速求出两个多项式/卷积相乘的结果
-
多项式
对于一个形如
[A(x)=a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+dots+a_0x^0=sum_{i=0}^{n-1}a_ix^i ]的式子,称其为一个多项式。其中最大的次数称为多项式的次数。
-
系数表示
将(n-1)次多项式的系数看做一个(n)维向量:
[vec a=(a_0,a_1,dots,a_{n-1}) ]即为多项式的系数表示
-
点值表示
对于一个(n-1)次多项式(A(x)),将(n)的不相同的(x)代入得到一系列点({(x_0,y_0)dots}),可以唯一确定多项式(A(x))
-
多项式乘法
对于两个多项式(A(x),B(x))
[A(x)=sum_{i=0}^{n-1}a_ix^i,B(x)=sum_{i=0}^{n-1}b_ix^i ]有(C(x)=A(x)* B(x))
[C(x)=sum_{i=0}^{2n-2}sum_{j+k=i}a_jb_kx^i ]
-
-
卷积
对于两个向量(vec a=(a_0,a_1,dots,a_{n-1}),vec b=(b_0,b_1,dots,b_{n-1}))
有卷积(vec aotimesvec b=c(c_0,c_1,dots,c_{2n-2}))
其中有(c_k=sum_{i,j}^{i+j=k}limits a_ib_j)
和上面多项式乘法非常类似。
那么如何计算多项式乘法呢?
一个显然的做法是按照定义(O(n^2))计算。
不过我们发现,对于两个点值表示({(ax_0,ay_0),dots},{(bx_0,by_0),dots}),可以(O(n))地相乘得到(C(x))的点值表达式。
那么有没有什么方法可以快速的将多项式转成点值表示和逆回来呢?
有的有的,请留下您的邮箱 (FFT)就可以做到这一点。
(FFT)大概包含(3)个步骤:
Part1
多项式 (Rightarrow) 点值表示 ((DFT,O(nlog_2n)))
Part2
点值表示相乘 ((O(n)))
Part3
点值表示 (Rightarrow) 多项式 ((IDFT,O(nlog_2n)))
Prepare
-
复数
复数由实部和虚部组成,例如(2+3i)(其中(i)为虚数单位,(i^2=sqrt{-1}))。可以把它理解为一个点或向量((2,3))。
复数运算法则:
-
加法
实部虚部分别相加
((2+3i)+(3+3i)=(5+6i))
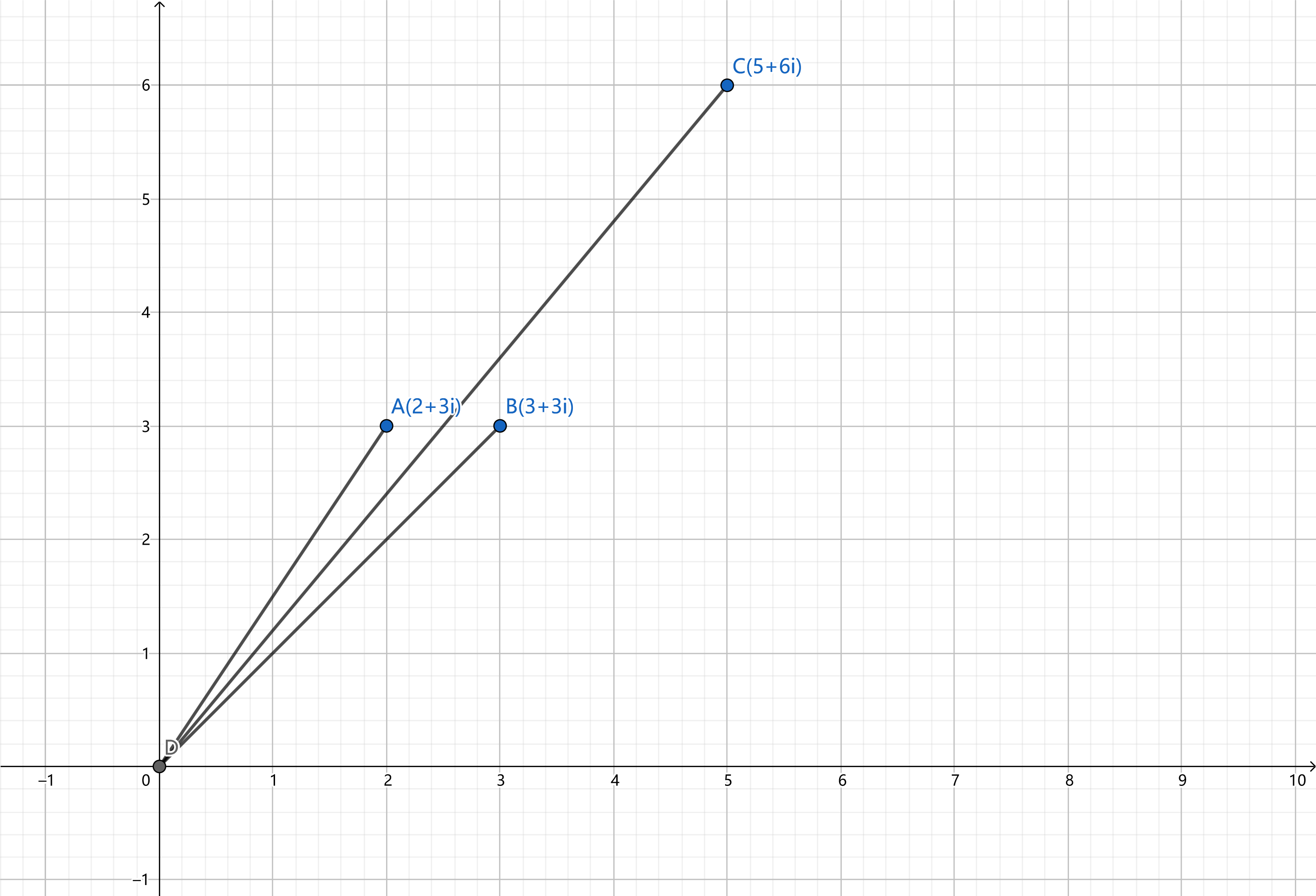
-
乘法
类似多项式乘法,在坐标系中直观表现为模长相乘,幅角相加(幅角为(x)轴逆时针转动的角度)。
((2+3i)* (3+3i)=6+6i+9i+9i^2=(-3+15i))
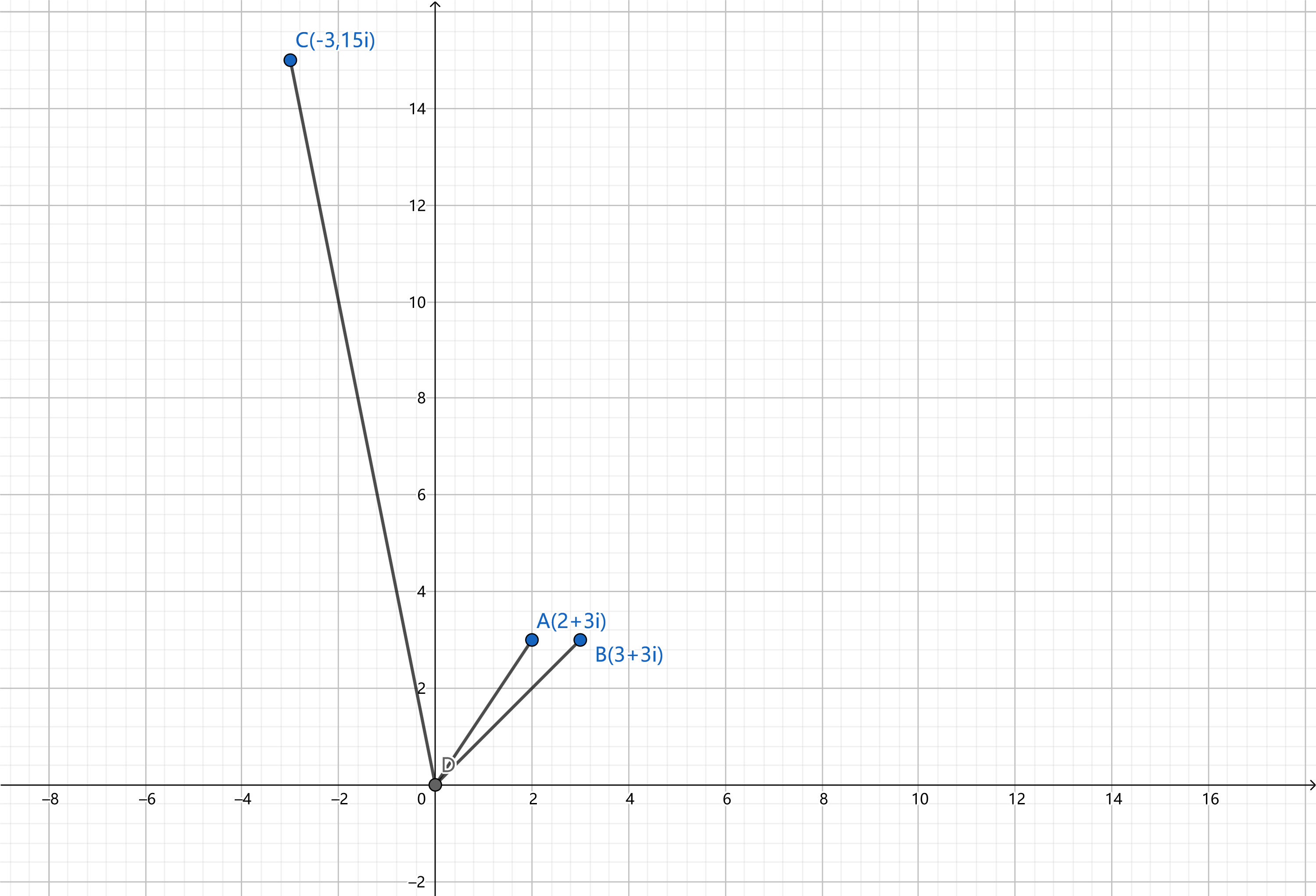
-
除法
类似分数的化简
(frac{2+3i}{3+3i}=frac{(2+3i)* (3-3i)}{(3+3i)* (3-3i)}=frac{6-6i+9i-9i^2}{9-9i^2}=frac{15+3i}{18}=frac{15}{18}+frac{3i}{18})
图就不画了,
太麻烦了。
-
-
思想
规定点值表示中的(n)个(x)值为(n)个模长为(1)的复数。
但是并不是随机的复数,是均匀分布在单位圆(以原点为圆心,半径为(1))上的(n)个复数,将圆(n)等分。
将点从(0)开始标号,设第(0)个点为(omega_n^0)(和我一起读,(Omegasim)),以此类推。
以((1,0))为起点,由复数乘法规则得:(omega_n^i)的模长一定是(1)。
则(omega_n^i)对应的点为((cos(frac{i}{n}2pi),sin(frac{i}{n}2pi)))。(采用弧度制)
把这些复数称为(n)次单位根。
接下来进入正题。
DFT (Discrete Fourier Transform)
(Q:)学了这么多,但是复杂度不还是(O(n^2))吗?
(A:)下面就介绍(O(nlog_2n))的算法。
-
(Cooley-Tukey)算法
发明者:(J. W. Cooley&J. W. Tukey)
思想:分治
使(n=2^m(min mathbb{Z})),若不够高位用(0)补齐(显然没有影响)。
接着,对于多项式(A(x)=sum_{i=0}^{n-1}limits a_ix^i),将其各项按次数奇偶性分类:
现在设:
则有:
对于(k<frac n2,)有:
同理,对于(k+frac n2)有:
因为(omega_n^{frac n2},omega_n^n) 分别对于着((-1,0),(1,0)),则
于是,问题被分成了更小的子问题,递归求解即可。
时间复杂度?这不某年初赛题吗 (T(n)=2T(frac n2)+O(n)=O(nlog_2n))
IDFT (Inverse Discrete Fourier Transform)
(Q:)既然把多项式变成了点值表示,那么怎么把它变回去呢??
首先,这个问题相当于解一个线性方程组:
写成矩阵:
求解矩阵逆我会,高斯消元
(O(n^3))是不可能的,这辈子都不可能的。
设上面式子中左边矩阵为(X)
现在考虑矩阵(Y,Y_{i,j}=(omega_n^{-i})^j,Z=X* Y)
则:
那么当(i=j)时
否则当(i ot=j)时
由等比数列求和公式:
那么就得到
((I)指单位矩阵)
也就是说,我们只要把(DFT)过程中的点值选取(omega_n^i)换成(omega_n^{-i}),进行一次(DFT)后把结果除以(n)就可以了。
时间复杂度证明同上。
那么这就是(FFT)的过程了。
是不是很简单啊。
代码实现
首先是最基本的(FFT)。
采用简单的递归实现。
时间复杂度 (O(nlog_2n))
空间复杂度 (O(nlog_2n))
代码:
#include <cmath>
#include <cstdio>
struct Complex//自定义复数,STL太慢
{
double x,y;//x为实部,y为虚部
inline Complex operator+(const Complex &a)//加法
{return (Complex){x+a.x,y+a.y};}
inline Complex operator-(const Complex &a)//减法
{return (Complex){x-a.x,y-a.y};}
inline Complex operator*(const Complex &a)//乘法
{return (Complex){x*a.x-y*a.y,x*a.y+y*a.x};}
//除法用不到就没写
}Pol[100005],Tmp[100005],Ome[100005],Inv[100005];
//Pol - 多项式 Tmp - 备用数组 Ome - 预处理omega_n^i Inv - Ome的逆
int n;//n=2^m
const double PI=acos(-1);
void Pre()
{
for(int i=0;i<n;++i)
{
Ome[i]=(Complex){cos(2.0*PI*i/n), sin(2.0*PI*i/n)};
Inv[i]=(Complex){cos(2.0*PI*i/n),-sin(2.0*PI*i/n)};
}//简单的预处理
}
void FFT(int Siz,int Lef,int Len)//Siz - 子问题大小 Lef - 区域最左端 Len - 步长(a0与a1的距离)
{
if(Siz==1)return;
int NSiz=Siz>>1;//下一个子问题
FFT(NSiz,Lef,Len<<1),FFT(NSiz,Lef+NSiz,Len<<1);//递归处理
for(int i=0;i<NSiz;++i)
{
int Pos=Len*i<<1;
Tmp[i]=Pol[Lef+Pos]+Ome[i*Len]*Pol[Lef+Pos+Len];//按照定义计算
Tmp[i+NSiz]=Pol[Lef+Pos]-Ome[i*Len]*Pol[Lef+Pos+Len];
}
for(int i=0;i<Siz;++i)Pol[Lef+i*Len]=Tmp[i];//计算完毕
}
int main(){Pre();FFT(n=65536,0,1);};
如果是(IDFT)把(FFT)中(Ome)改成(Inv)最后结果(/n)即可。
但是。。这个程序常数太大了!!(自带O(Inf)大常数)
我们来尝试优化程序。
非递归实现
发现,第一层递归将下标二进制中最后一位相同的元素分在了一起。(按奇偶性分类)
第二层将最后两位相同的分在了一起。
于是,同一组数二进制反转后是一段连续的区间(前几位相同,后几位包含所有情况)。
发现,(i)最后所在的位置是(R_i)((i)的二进制反转)
先把所有数放到最后的位置上,最后向上合并即可。
时间复杂度 (O(nlog_2n))
空间复杂度 (O(nlog_2n))
代码:
#include <cmath>
#include <cstdio>
#include <algorithm>
struct Complex//自定义复数,STL太慢
{
double x,y;//x为实部,y为虚部
inline Complex operator+(const Complex &a)//加法
{return (Complex){x+a.x,y+a.y};}
inline Complex operator-(const Complex &a)//减法
{return (Complex){x-a.x,y-a.y};}
inline Complex operator*(const Complex &a)//乘法
{return (Complex){x*a.x-y*a.y,x*a.y+y*a.x};}
//除法用不到就没写
}Pol[100005],Ome[100005],Inv[100005];
//Pol - 多项式 Ome - 预处理omega_n^i Inv - Ome的逆
int n;//n=2^m
const double PI=acos(-1);
void Pre()
{
for(int i=0;i<n;++i)
{
Ome[i]=(Complex){cos(2.0*PI*i/n), sin(2.0*PI*i/n)};
Inv[i]=(Complex){cos(2.0*PI*i/n),-sin(2.0*PI*i/n)};
}//简单的预处理
}
void FFT(Complex op[])
{
for(int i=0,j=0;i<n;++i)
{
if(i>j)std::swap(Pol[i],Pol[j]);//避免重复交换
for(int l=n>>1;(j^=l)<l;l>>=1);//反向二进制加法
}
for(int i=2;i<=n;i<<=1)//现在处理的区间长度(从下往上)
{
int m=i>>1;//区间子问题
for(int j=0;j<n;j+=i)//对每一个区间计算一边
for(int k=0;k<m;++k)//此区间的左边(k<i/2)
{
Complex Tmp=op[n/i*k]*Pol[j+k+m];//避免额外内存开销(蝴蝶操作)
Pol[j+k+m]=Pol[j+k]-Tmp;
Pol[j+k]=Pol[j+k]+Tmp;
}
}
}
int main(){n=65536;Pre();FFT(Ome);FFT(Inv);};
(En,)模板题。
因为乘起来有(n+m)次,要补足(n+m)。
时间复杂度 (O(nlog_2n))
空间复杂度 (O(nlog_2n))
代码:
#include <cmath>
#include <cstdio>
#include <cctype>
#include <algorithm>
char File[1000005],*p1=File,*p2=File;
inline char Getchar()
{
return p1==p2&&(p2=(p1=File)+fread(File,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
inline int Getint()
{
register int x=0,c;
while(!isdigit(c=Getchar()));
for(;isdigit(c);c=Getchar())x=x*10+(c^48);
return x;
}
struct Complex
{
double x,y;
inline Complex operator+(const Complex &a)
{return (Complex){x+a.x,y+a.y};}
inline Complex operator-(const Complex &a)
{return (Complex){x-a.x,y-a.y};}
inline Complex operator*(const Complex &a)
{return (Complex){x*a.x-y*a.y,x*a.y+y*a.x};}
}a[3000005],b[3000005],Ome[3000005],Inv[3000005];
int n,m,Maxl;
const double PI=acos(-1);
void Pre()
{
for(register int i=0;i<n;++i)
{
Ome[i]=(Complex){cos(2.0*PI*i/n),sin(2.0*PI*i/n)};
Inv[i]=(Complex){cos(2.0*PI*i/n),sin(2.0*PI*-i/n)};
}
}
void FFT(Complex Pol[],Complex op[])
{
for(int i=0,j=0;i<n;++i)
{
if(i>j)std::swap(Pol[i],Pol[j]);
for(int l=n>>1;(j^=l)<l;l>>=1);
}
for(register int i=2;i<=n;i<<=1)
{
int m=i>>1;
for(register int j=0;j<n;j+=i)
for(register int k=0;k<m;++k)
{
Complex Tmp=op[n/i*k]*Pol[j+k+m];
Pol[j+k+m]=Pol[j+k]-Tmp;
Pol[j+k]=Pol[j+k]+Tmp;
}
}
}
int main()
{
n=Getint(),m=Getint();
for(register int i=0;i<=n;++i)a[i].x=Getint();
for(register int i=0;i<=m;++i)b[i].x=Getint();
for(Maxl=n+m,n=2;n<=Maxl;n<<=1);
Pre();
FFT(a,Ome),FFT(b,Ome);
for(int i=0;i<n;++i)a[i]=a[i]*b[i];
FFT(a,Inv);
for(int i=0;i<=Maxl;++i)printf("%d%c",(int)floor(a[i].x/n+0.5),i==Maxl?'
':' ');
return 0;
}
我终于会写A*B了!!
把(x)看成(10)多项式乘法即可。
代码:
#include <cmath>
#include <cstdio>
#include <cctype>
#include <algorithm>
char File[1000005],*p1=File,*p2=File;
inline int Getint()
{
register int c;
while(!isdigit(c=getchar()));
return c^48;
}
struct Complex
{
double x,y;
inline Complex operator+(const Complex &a)
{return (Complex){x+a.x,y+a.y};}
inline Complex operator-(const Complex &a)
{return (Complex){x-a.x,y-a.y};}
inline Complex operator*(const Complex &a)
{return (Complex){x*a.x-y*a.y,x*a.y+y*a.x};}
}a[150005],b[150005],Ome[150005],Inv[150005];
int n,Maxl,s[150005];
const double PI=acos(-1);
void Pre()
{
for(register int i=0;i<n;++i)
{
Ome[i]=(Complex){cos(2.0*PI*i/n),sin(2.0*PI*i/n)};
Inv[i]=(Complex){cos(2.0*PI*i/n),sin(2.0*PI*-i/n)};
}
}
void FFT(Complex Pol[],Complex op[])
{
for(int i=0,j=0;i<n;++i)
{
if(i>j)std::swap(Pol[i],Pol[j]);
for(int l=n>>1;(j^=l)<l;l>>=1);
}
for(register int i=2;i<=n;i<<=1)
{
int m=i>>1;
for(register int j=0;j<n;j+=i)
for(register int k=0;k<m;++k)
{
Complex Tmp=op[n/i*k]*Pol[j+k+m];
Pol[j+k+m]=Pol[j+k]-Tmp;
Pol[j+k]=Pol[j+k]+Tmp;
}
}
}
int main()
{
scanf("%d",&n),--n;
for(register int i=n;i>=0;--i)a[i].x=Getint();
for(register int i=n;i>=0;--i)b[i].x=Getint();
for(Maxl=n<<1,n=2;n<=Maxl;n<<=1);
Pre();
FFT(a,Ome),FFT(b,Ome);
for(int i=0;i<n;++i)a[i]=a[i]*b[i];
FFT(a,Inv);
for(int i=0;i<=Maxl+5;++i)
{
s[i]+=(int)floor(a[i].x/n+0.5);
s[i+1]+=s[i]/10;
s[i]%=10;
}
bool OK=false;
for(int i=Maxl+5;i>=0;--i)
{
if(s[i])OK=true;
if(OK||!i)putchar(s[i]^48);
}
puts("");
return 0;
}
总结
(FFT)太可怕了。。虽然联赛不至于考((Flag)),但是还是很有用的,巩固一下。
参考资料:((Dalao Orz))
FFT 相关优化(Update in 2019/8/6)
-
首先是奇怪的IO优化和
register+inline乱搞?但后者作用并不大 -
一种方法是多次利用一个DFT后的多项式:
例如对于多项式(A,B,C),现在需要求(A*B,A*C)
显然可以先计算(A*B),再计算(A*C)
但观察到两次计算中都对(A)进行了一次DFT,这显然是浪费的,所以我们可以将(A)的DFT预处理出来备用。
不过以上两种方式优化都不明显,且局限性较大,接下来介绍一种新的方法:"DFT合并"
假设现在对长度为(n)((2)的整次幂)的多项式(A,B)进行DFT,设:
其中(F_p,F_q)即是(P,Q) DFT后的序列。
则有:
为了方便表示,设(X=2pi*frac{jk}n,conj(v))表示(v)的共轭复数(实部相等,虚部相反),有:
那么你就会发现,只需一次DFT就可以得到(F_p,F_q),然后有:
((DFT(B))后面是为了避免复数除法)
于是我们就减少了一次DFT的时间
(Hint:此方法对精度要求较高,建议使用long double,不过在整数FFT显然够用)
代码:
效果:2.46s->2.08s
可能还是我tcl吧
这个代码可能和我以前的FFT不太一样?
// luogu-judger-enable-o2
#include <cmath>
#include <cstdio>
#include <cctype>
#include <algorithm>
#define rint register int
//Having A Daydream...
char In[1<<20],*p1=In,*p2=In;
#define Getchar (p1==p2&&(p2=(p1=In)+fread(In,1,1<<20,stdin),p1==p2)?EOF:*p1++)
inline int Getint()
{
register int x=0,c;
while(!isdigit(c=Getchar));
for(;isdigit(c);c=Getchar)x=x*10+(c^48);
return x;
}
char Out[22222222],*Outp=Out,St[22],*Tp=St;
inline void Putint(int x)
{
do *Tp++=x%10^48;while(x/=10);
do *Outp++=*--Tp;while(St!=Tp);
}
struct Complex
{
double x,y;
inline Complex operator+(const Complex &o)const{return (Complex){x+o.x,y+o.y};}
inline Complex operator-(const Complex &o)const{return (Complex){x-o.x,y-o.y};}
inline Complex operator*(const Complex &o)const{return (Complex){x*o.x-y*o.y,x*o.y+y*o.x};}
inline Complex operator/(const double k)const{return (Complex){x/k,y/k};}
inline Complex Conj(){return (Complex){x,-y};}
}I=(Complex){0,1};
int n,m,l,r[1<<21];
Complex a[1<<21],b[1<<21],Ome[1<<21],Inv[1<<21];
Complex Fp[1<<21],Fq[1<<21];
const double Pi=acos(-1),e=exp(1),Eps=1e-8;
void FFT(Complex *A,Complex *Op)
{
for(rint i=0;i<n;++i)if(i<r[i])std::swap(A[i],A[r[i]]);
for(rint i=2;i<=n;i<<=1)
for(rint j=0,m=i>>1;j<n;j+=i)
for(rint k=0;k<m;++k)
{
Complex Tmp=Op[n/i*k]*A[j+m+k];
A[j+m+k]=A[j+k]-Tmp;
A[j+k]=A[j+k]+Tmp;
}
}
int main()
{
freopen("in.txt","r",stdin);
n=Getint(),m=Getint();
for(rint i=0;i<=n;++i)a[i].x=Getint();
for(rint i=0;i<=m;++i)b[i].x=Getint();
for(m=n+m,n=2,l=1;n<=m;n<<=1,++l);
for(rint i=0;i<n;++i)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
for(rint i=0;i<n;++i)
{
double x=cos(2*Pi*i/n),y=sin(2*Pi*i/n);
Ome[i]=(Complex){x,y},Inv[i]=(Complex){x,-y};
}
for(rint i=0;i<n;++i)Fp[i]=a[i]+I*b[i];
FFT(Fp,Ome);
for(rint i=0;i<n;++i)Fq[i]=(i?Fp[n-i]:Fp[0]).Conj();//Fp[n]=Fp[0]
for(rint i=0;i<n;++i)a[i]=(Fp[i]+Fq[i])/2,b[i]=(Fp[i]-Fq[i])*I/-2;
for(rint i=0;i<n;++i)a[i]=a[i]*b[i];
FFT(a,Inv);
for(rint i=0;i<=m;++i)Putint(int(a[i].x/n+0.5)),*Outp++=i==m?'
':' ';
return fwrite(Out,1,Outp-Out,stdout),0;
}
其实还有继续往下的优化方法,参考毛神论文。不过作用不大,就没学了,一般的题目不会考这种东西。
参考资料:
再探快速傅里叶变换 - 毛啸 (2016国家集训队论文)