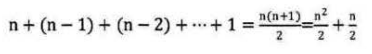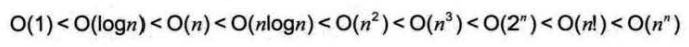算法的复杂性是算法运行所以需要的计算机资源的量,需要时间资源的量称为时间复杂性,需要空间资源的量称为空间复杂性。此量应只依赖算法要解决问题的规模、算法的输入和算法本身,分别用N,I和A表示,用C表示复杂性,应有C=F(N,I,A),若将时间和空间分开,分别用T和S表示,且A通常隐含在复杂性函数名中,因而将T和S简写为T=T(N,I)和S=(N,I)。
时间复杂度
复杂函数具象化。
根据T(N,I)概念,它应该是算法在一台抽象计算机上运行所需时间。
设此计算机提供元运算共k种,它们分别记为O1,O2,...,Ok。
又设每执行一次这些元运算所需时间分别为t1,t2,...,tk。
对于给定算法A,设经统计用到元运算Oi的次数为ei,i=1,2,...,k。
因此,对于每个i,1<=i<=k,ei是N和I的函数,即ei=ei(N,I)。因此,T(N,I)=∑ti*ei(N,I)。其中,ti(i=1,2,3,..,k)是与N和I无关的常数。
不可能对规模N的每个合法输入I都统计ei(N,I),i=1,2,...,k。因此,T(N,I)还需进步简化。或者说,只能对N的某些或某类代表性合法输入统计相应ei来评价时间复杂度。如下分别为最坏、最好、平均时间复杂度:
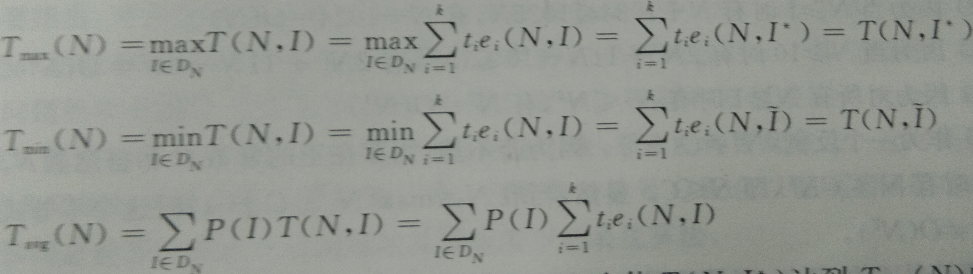
其中DN是规模为N的合法输入集合;I*是式一合法输入;I~是式二合法输入;而P(N)是算法的应用中出现输入I的概率。其中最有价值的是最坏时间复杂度。
设T(N)为关于算法A的复杂性函数。若有N->∞时有(T(N)-T'(N))/T'(N) -> 0,那么,就说T'(N)是T(N)当N->∞时的渐进性态。即T'(N)是T(N)当N->∞时的渐进表达式,也就是其略去低阶项所留下的主项,更加简单,即对其的简化。
进一步简化。常常比较阶来判断算法复杂度效率高低,所以常常假设算法中用到的所有不同的元运算各执行一次所需要的时间都是一个单位时间。
如下引入渐进意义下的记号:O,Ω,θ,ο
若存在正常数C和自然数N0,使当N>=N0时有f(N)<=Cg(N),则称函数f(N)当N充分大时上有界,且g(N)是它一个上届,记为f(N)=O(g(N)),且说f(N)阶不高于g(N)阶。举例:
1、对所有N>=1时有3N<=4N,有3N=O(N)
2、当N>=1时有N+1024<=1025N,有N+1024=O(N)
3、当N>=10时有2N^2+11N-10<=3N^2,有2N^2+11N-10=O(N^2)
根据O的定义,易证明它有下运算:
1、O(f)+O(g)=O(max(f,g))
2、O(f)+O(g)=O(f+g)
3、O(f)O(g)=O(fg)
4、若g(N)=O(f(N)),则O(f)+O(g)=O(f)
5、O(Cf(N))=O(f(N)),其中C是一个正常数
6、f=O(f)
则Ω为下届,θ为同阶,f(N)=o(g(N))则表示f(N)当N充分大时阶比g(N)低。
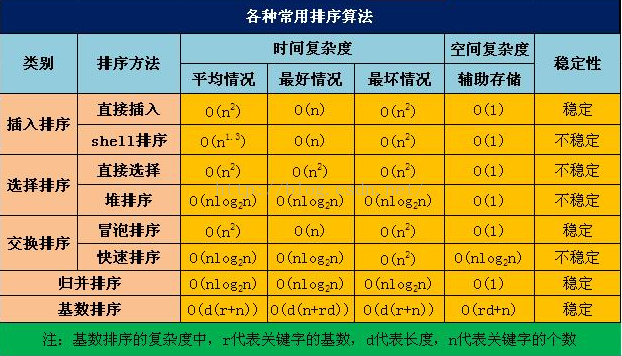
常见复杂度函数比较

masterd定理
假设有递推关系式![]() ,其中n 为问题规模,
,其中n 为问题规模,![]() 为递推的子问题数量,
为递推的子问题数量,![]() 为每个子问题的规模(假设每个子问题的规模基本一样),
为每个子问题的规模(假设每个子问题的规模基本一样),![]() 为递推以外进行的计算工作。a≥1,b>1为常数,f(n) 为函数,T(n) 为非负整数。则有以下结果(分类讨论):
为递推以外进行的计算工作。a≥1,b>1为常数,f(n) 为函数,T(n) 为非负整数。则有以下结果(分类讨论):
如下转自:https://www.cnblogs.com/silence-x/p/10544072.html
一、算法的时间复杂度定义
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度,也就是算法的时间量度。记作:T(n)=O(f(n))。它表示随问题n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称为时间复杂度。其中,f(n)是问题规模n的某个函数。
这样用大写O()来体现算法时间复杂度的记法,我们称之为大0记法。
二、推导大O阶方法
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
三、推导示例
1、常数阶
首先顺序结构的时间复杂度。下面这个算法,是利用高斯定理计算1,2,……n个数的和。
1 int sum = 0, n = 100; /*执行一次*/
2
3 sum = (1 + n) * n / 2; /*执行一次*/
4
5 printf("%d",sum); /*执行一次*/
这个算法的运行次数函数是f (n) =3。 根据我们推导大0阶的方法,第一步就是把常数项3 改为1。在保留最高阶项时发现,它根本没有最高阶项,所以这个算法的时间复杂度为0(1)。
另外,我们试想一下,如果这个算法当中的语句 sum = (1+n)*n/2; 有10 句,则与示例给出的代码就是3次和12次的差异。这种与问题的大小无关(n的多少),执行时间恒定的算法,我们称之为具有O(1)的时间复杂度,又叫常数阶。对于分支结构而言,无论是真,还是假,执行的次数都是恒定的,不会随着n 的变大而发生变化,所以单纯的分支结构(不包含在循环结构中),其时间复杂度也是0(1)。
2、线性阶
线性阶的循环结构会复杂很多。要确定某个算法的阶次,我们常常需要确定某个特定语句或某个语句集运行的次数。因此,我们要分析算法的复杂度,关键就是要分析循环结构的运行情况。
下面这段代码,它的循环的时间复杂度为O(n), 因为循环体中的代码须要执行n次。
1 int i;
2
3 for(i = 0; i < n; i++){
4
5 /*时间复杂度为O(1)的程序步骤序列*/
6
7 }
3、对数阶
如下代码:
1 int count = 1;
2
3 while (count < n){
4
5 count = count * 2;
6
7 /*时间复杂度为O(1)的程序步骤序列*/
8
9 }
由于每次count乘以2之后,就距离n更近了一分。 也就是说,有多少个2相乘后大于n,则会退出循环。 由2^x=n 得到x=logn。 所以这个循环的时间复杂度为O(logn)。
4、平方阶
下面例子是一个循环嵌套,它的内循环刚才我们已经分析过,时间复杂度为O(n)。
1 int i, j;
2
3 for(i = 0; i < n; i++){
4
5 for(j = 0; j < n; j++){
6
7 /*时间复杂度为O(1)的程序步骤序列*/
8
9 }
10
11 }
而对于外层的循环,不过是内部这个时间复杂度为O(n)的语句,再循环n次。 所以这段代码的时间复杂度为O(n^2)。
如果外循环的循环次数改为了m,时间复杂度就变为O(mXn)。
所以我们可以总结得出,循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。
那么下面这个循环嵌套,它的时间复杂度是多少呢?
1 int i, j;
2
3 for(i = 0; i < n; i++){
4
5 for(j = i; j < n; j++){ /*注意j = i而不是0*/
6
7 /*时间复杂度为O(1)的程序步骤序列*/
8
9 }
10
11 }
由于当i=0时,内循环执行了n次,当i = 1时,执行了n-1次,……当i=n-1时,执行了1次。所以总的执行次数为:
用我们推导大O阶的方法,第一条,没有加法常数不予考虑;第二条,只保留最高阶项,因此保留时(n^2)/2; 第三条,去除这个项相乘的常数,也就是去除1/2,最终这段代码的时间复杂度为O(n2)。
从这个例子,我们也可以得到一个经验,其实理解大0推导不算难,难的是对数列的一些相关运算,这更多的是考察你的数学知识和能力。
5、立方阶
下面例子是一个三重循环嵌套。
1 int i, j;
2
3 for(i = 1; i < n; i++)
4
5 for(j = 1; j < n; j++)
6
7 for(j = 1; j < n; j++){
8
9 /*时间复杂度为O(1)的程序步骤序列*/
10
11
12
13 }
这里循环了(1^2+2^2+3^2+……+n^2) = n(n+1)(2n+1)/6次,按照上述大O阶推导方法,时间复杂度为O(n^3)。
四、常见的时间复杂度
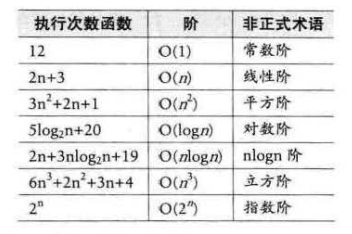
常见的时问复杂度如表所示。
常用的时间复杂度所耗费的时间从小到大依次是:
我们前面已经谈到了。O(1)常数阶、O(logn)对数阶、O(n)线性阶、 O(n^2)平方阶等,像O(n^3),过大的n都会使得结果变得不现实。同样指数阶O(2^n)和阶乘阶O(n!)等除非是很小的n值,否则哪怕n 只是100,都是噩梦般的运行时间。所以这种不切实际的算法时间复杂度,一般我们都不去讨论。
五、最坏情况与平均情况
我们查找一个有n 个随机数字数组中的某个数字,最好的情况是第一个数字就是,那么算法的时间复杂度为O(1),但也有可能这个数字就在最后一个位置上待着,那么算法的时间复杂度就是O(n),这是最坏的一种情况了。
最坏情况运行时间是一种保证,那就是运行时间将不会再坏了。 在应用中,这是一种最重要的需求, 通常, 除非特别指定, 我们提到的运行时间都是最坏情况的运行时间。
而平均运行时间也就是从概率的角度看, 这个数字在每一个位置的可能性是相同的,所以平均的查找时间为n/2次后发现这个目标元素。平均运行时间是所有情况中最有意义的,因为它是期望的运行时间。也就是说,我们运行一段程序代码时,是希望看到平均运行时间的。可现实中,平均运行时间很难通过分析得到,一般都是通过运行一定数量的实验数据后估算出来的。一般在没有特殊说明的情况下,都是指最坏时间复杂度。
六、算法空间复杂度
我们在写代码时,完全可以用空间来换取时间,比如说,要判断某某年是不是闰年,你可能会花一点心思写了一个算法,而且由于是一个算法,也就意味着,每次给一个年份,都是要通过计算得到是否是闰年的结果。 还有另一个办法就是,事先建立一个有2050个元素的数组(年数略比现实多一点),然后把所有的年份按下标的数字对应,如果是闰年,此数组项的值就是1,如果不是值为0。这样,所谓的判断某一年是否是闰年,就变成了查找这个数组的某一项的值是多少的问题。此时,我们的运算是最小化了,但是硬盘上或者内存中需要存储这2050个0和1。这是通过一笔空间上的开销来换取计算时间的小技巧。到底哪一个好,其实要看你用在什么地方。
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作:S(n)= O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
一般情况下,一个程序在机器上执行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元,若输入数据所占空间只取决于问题本身,和算法无关,这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数,则称此算法为原地工作,空间复杂度为0(1)。
通常, 我们都使用"时间复杂度"来指运行时间的需求,使用"空间复杂度"指空间需求。当不用限定词地使用"复杂度'时,通常都是指时间复杂度。
七、一些计算的规则
1、加法规则
T(n,m) = T1(n) + T2(m) = O(max{f(n), g(m)})
2、乘法规则
T(n,m) = T1(n) * T2(m) = O(max{f(n)*g(m)})
3、一个经验
复杂度与时间效率的关系:
c(常数) < logn < n < n*logn < n^2 < n^3 < 2^n < 3^n < n!
l------------------------------l--------------------------l--------------l
较好 一般 较差