前言
我经常见到这样一类贪心的问题,我一看就不会,想一会还是不会,看题解,上来就是一句 “按照xxx排序,然后xxx,就完了”
那我怎么知道按什么排序呢?有的时候可以靠人的感觉,那我的感觉不灵了咋办呢?
一些考虑方法
对于一类重点考虑选择顺序的问题,我们可以假设A在B前面比B在A前面更优,得到一些不等式,化简一下,看一看它们有怎么样的关系,从而得到最优策略是什么样的。
一些例子
这里的例子都比较简单,但是我想要强调的是考虑问题的方法,而不是问题本身有多难。
有的时候不能轻视简单的问题,因为你可能会忽略一些细节;而这些细节恰恰可能是复杂问题中的解题关键
经典题1
有一个数列 (a_{1...n}),重新排列使得 (sumlimits_{i=1}^{n} ia_i) 最大。
我们当然可以由排序不等式直接得结论,但是如果自己做,怎么做呢?
假设最优解中有两个位置 (x,y),不妨令 (x<y),那么如果交换 (x,y) 的位置,一定不会变优。(显然,毕竟是最优解)
换句话说就是 (xa_x+ya_yge ya_x+xa_y)
(x(a_x-a_y)ge y(a_x-a_y))
((a_x-a_y)(x-y)ge 0)
由于 (x<y),所以 (a_xle a_y)。
于是我们得到,最优解中,左边的数都比右边的数小。如何达到最优解呢?排个序就行了。
经典题2 [JSOI2007]建筑抢修
这题就是我说的那个题解上来就按xxx排序的
大家都知道这题的做法是按deadline排序然后反悔贪心,怎么来的?
设某个任务耗时是 (a_i),dealine 是 (d_i)。设 (A(a_1,d_1), B(a_2,d_2))。不妨令 (A) 排在 (B) 的前面。假设交换位置后悔变劣,看看会怎么样。
那既然换一下会变劣,肯定是原来 (A,B) 两个都可以,换一下之后排在后面的 (A) 不行了。
排在前面的 (B) 肯定是可以的,毕竟原来都可以,换到更前面显然还是可以的。
图大概是这样
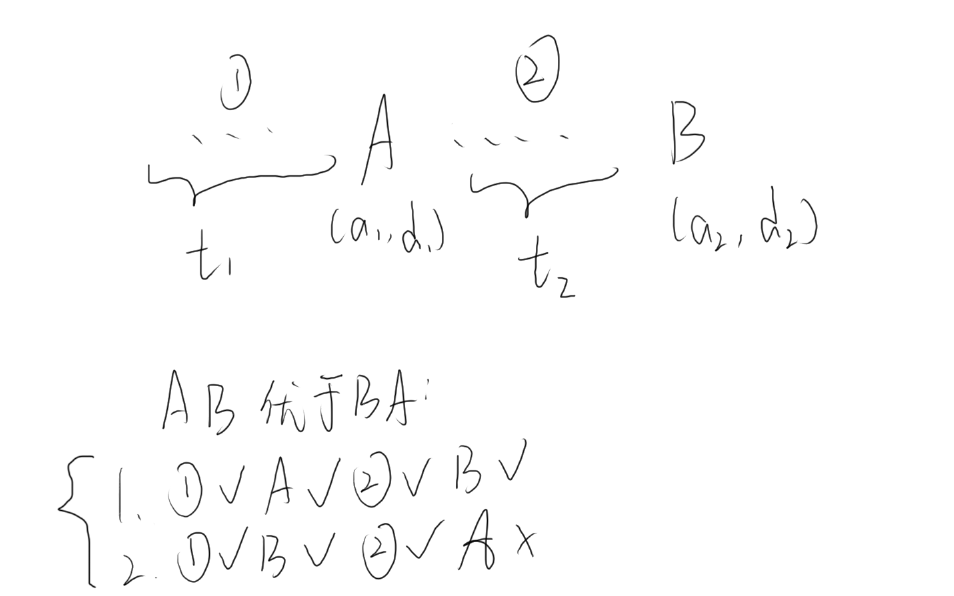
设 (A) 前面的耗时总共为 (t_1),(A,B) 之间的耗时总共为 (t_2)。可得:
- (t_1+a_1le d_1),(t_1+a_1+t_2+a_2le d_2)
- (t_1+a_2le d_2),(t_1+a_2+t_2+a_1>d_1)
我们发现,同一个东西 (t_1+a_1+t_2+a_2),不严格比 (d_2) 小,严格比 (d_1) 大。那么 (d_1<d_2)
那我们就得出来了,我们要按 deadline 排序。
但是注意到这里还有一个能不能选的问题,排完序后不是扫一遍就可以的,还要再贪心一下。
对于一个任务,如果能选,不选肯定亏了,显然要选。如果不能选(时间超了),看看换掉前面的行不行。设前面选的最大的为 (a_{mx}),当前是 (a_i)。如果 (a_{mx}>a_i),那它就不该出现 —— 毕竟它让 (a_i) 不能做了,换掉它之后,(a_i) 再加上,总用时比原来还小,肯定还是合法的。不但没少完成,并且时间更少,更有利于后面继续完成。但是如果 (a_{mx}le a_i),那说明换了之后也不会变优,甚至会变劣,肯定不换,直接不做了。
后记
以后会更一些更加有意思的题,也许