Codeforces Round #635 (Div. 2) E. Kaavi and Magic Spell 区间dp

https://codeforces.ml/contest/1337/problem/E

给出两个字符串 s和t ，字符串s的长度大于等于t的长度，和一个空字符串A；

可以执行两种操作：

1.将s的第一个字符删除并加到A字符串的前面；

2.将s的第一个字符删除并加到A字符串的后面；

求此过程中A的前缀等于t的个数并mod998244353；

例如：

s:abab

t:ba

结果为12

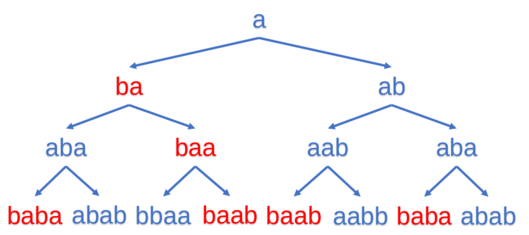
当A字符串一开始未加入a的时候为空串，所以加入a也有两种方法，在空串前和空串后，因此答案为 6*2=12。（一开始死活没理解这一点，案例怎么算都不对，，，狗头）

思路：把t字符串当作长度为n的字符串，(m,n]之间的字符随意，先把A字符串前m个字符串固定，算出前m个字符串的情况，后面的字符随意；

区间dp，dp[l][r]代表A和t的区间[l,r]的字符相匹配的串的个数，先枚举s[i],i同时也是区间长度，长度从1开始，匹配完长度为1的字符串，再匹配长度为2的字符串，那么当我们匹配长度为3的字符串时，只需要判断一个字符就可以了，其中两个字符已经匹配好了，当我们新添加一个字符时，分别比较当前字符和tl字符是否相等，和tr字符是否相等.

dp方程：

当 s[i]==t[l]或者l>m时：dp[l][r]=(dp[l][r]+dp[l+1][r])%mod;

当s[i]==t[r]或者r>m时：dp[l][r]=(dp[l][r]+dp[l][r-1])%mod;

dp[1][m~n]的值相加就是答案。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=3e3+5;
const ll mod=998244353;
const int inf=0x3f3f3f3f;
const long long INF=0x3f3f3f3f3f3f3f3f;
char s[MAXN],t[MAXN];
ll dp[MAXN][MAXN];
int main()
{
    scanf("%s%s",s+1,t+1);
    int n=strlen(s+1);
    int m=strlen(t+1);
    for(int i=1;i<=n+1;i++)dp[i][i-1]=1;
    for(int i=1;i<=n;i++)//枚举 字符串s + 区间长度
    {
        for(int l=1,r=l+i-1;r<=n;l++,r++)//枚举区间 [l,r]
        {
            if(s[i]==t[l]||l>m)dp[l][r]=(dp[l][r]+dp[l+1][r])%mod;
            if(s[i]==t[r]||r>m)dp[l][r]=(dp[l][r]+dp[l][r-1])%mod;
        }
    }
    ll ans=0;
    for(int i=m;i<=n;i++)ans=(ans+dp[1][i])%mod;
    printf("%lld
",ans);
    return 0;
}