快速排序（Quick Sort）

标签

非稳定排序、原地排序、比较排序

基本思想

冒泡排序是在相邻的两个记录进行比较和交换，每次交换只能上移或下移一个位置，导致总的比较与移动次数较多。快速排序是目前应用最广泛的排序算法之一。快速排序又称分区交换排序，是对冒泡排序的改进，快速排序采用的思想是分治思想。

每次从待排序区间选取一个元素（一般有多种选取规则，越接近排序后的中位算法效果越好，因为递归树越平衡）作为基准记录，所有比基准记录小的元素都在基准记录的左边，而所有比基准记录大的元素都在基准记录的右边。之后分别对基准记录的左边和右边两个区间进行快速排序，直到将整个线性表排序完成。

算法描述

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

• 步骤1：从数列中挑出一个元素，称为 “基准”（pivot）；
• 步骤2：重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
• 步骤3：递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

动图演示

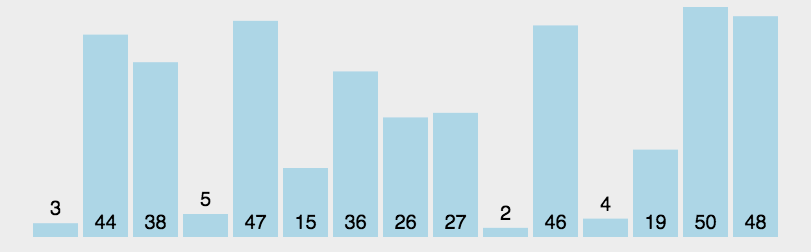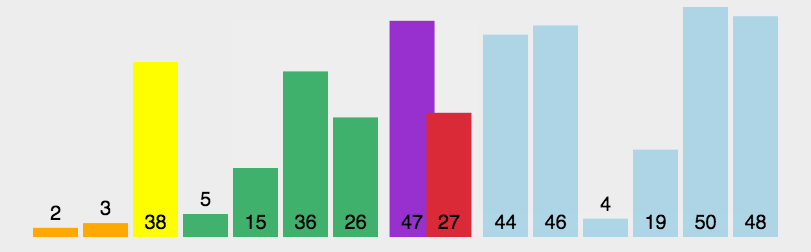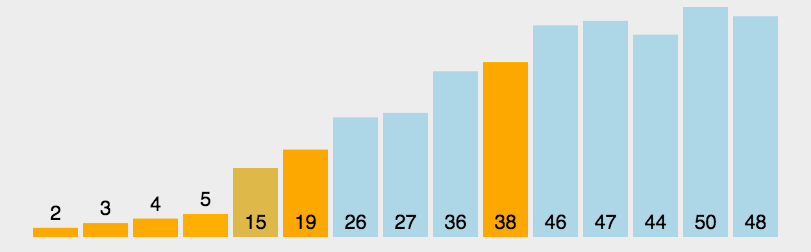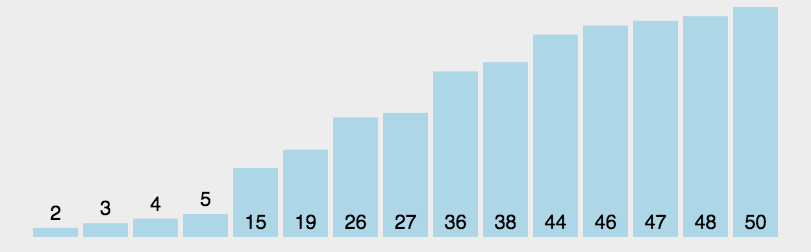
时间复杂度

最好情况：是每趟排序结束后，每次划分使两个子文件的长度大致相等，时间复杂度为$O(nlog n)$。

最坏情况：是待排序记录已经排好序，第一趟经过$n - 1$次比较后第一个记录保持位置不变，并得到一个$n - 1$个元素的子记录；第二趟经过$n - 2$次比较，将第二个记录定位在原来的位置上，并得到一个包括$n - 2$个记录的子文件，依次类推，这样总的比较次数是：$C_{max} = sum_{i = 1}^{n − 1} (n − i) = n(n − 1) / 2 = O(n^2)%。

可通过随机选取基准值来尽可能避免最坏情况。

平均情况：$O(nlog n)$

空间复杂度

没有额外的空间开销。

算法示例

基本迭代实现

左右交替扫描、替换。递归子序列。

void quick_sort_v1(int *arr, int l, int r) {
    if (l >= r) return;
    int x = l, y = r, z = arr[l]; //基准值默认为最左边第一个
    while(x < y) {
        while (x < y && arr[y] >= z) --y;
        if (x < y) arr[x++] = arr[y];
        while (x < y && arr[x] <= z) ++x;
        if (x < y) arr[y--] = arr[x];    
    }
    arr[x] = z;
    quick_sort_v1(arr, l, x - 1);
    quick_sort_v1(arr, x + 1, r);
    return;
}

单边递归优化

减少一边函数调用的代价。

void quick_sort_v2(int *arr, int l, int r) {
    while (l < r) {
        int x = l, y = r, z =arr[l];
        while (x < y) {
            while (x < y && arr[y] >= z) --y;
            if (x < y) arr[x++] = arr[y];
            while (x < y && arr[x] <= z) ++x;
            if (x < y) arr[y--] = arr[x];
        }
        arr[x] = z;
        quick_sort_v2(arr, l, x -1);
        l = x + 1;
    }     
    return;
}

无监督优化

与机器学习中通常的无监督概念不同，此处的无监督是指“去监督项”的意思。对于需要频繁检查条件的程序来说，减少一个监督项的检查，可以显著提升性能。

详细示例见插入排序的无监督优化部分。

void quick_sort_v3(int *arr, int l, int r) {
    while (l < r) {
        int x = l, y = r, z = arr[l];
        do {
            //减少了监督项
            while (x < r && arr[x] <= z) ++x;
            while (y > l && arr[y] >= z) --y;
            if (x < y) {
                swap(arr[x], arr[y]);
                ++x;
                --y;
            }
        } while (x <= y && x < right);
        arr[l] = arr[y];
        arr[y] = z;
        quick_sort_v3(arr, l, y - 1);
        l = y + 1;
    } 
    return;
}

随机基准值

依据递归树越平衡（矮）效率越高的思路，基准值的选取越靠近实际排序后的中位数快排算法的效率越好。

所以将基准值的选取方案由最左端改为随机（数据量越大，随机的效果越好）。

void quick_sort_v4(int *arr, int l, int r) {
    while (l < r) {
        int rnum = l + rand()%(r - l + 1); //基准值随机选取
        int x = l, y = r, z = arr[rnum];
        do {
            //减少了监督项
            while (x < r && arr[x] <= z) ++x;
            while (y > l && arr[y] >= z) --y;
            if (x < y) {
                swap(arr[x], arr[y]);
                ++x;
                --y;
            }
        } while (x <= y && x < right);
        arr[rnum] = arr[y];
        arr[y] = z;
        quick_sort_v4(arr, l, y - 1);
        l = y + 1;
    } 
    return;
}        

中位数基准值

基准值选取的另一种方案。因为位置处于中间，此时单边递归和无监督优化后的边界判断相较于基准值位于最左端来说要简洁不少，所以该方案更适合优化后的基准值选取。

int median(int *arr, int l, int r) {
    int x = arr[l], y = arr[r], z = arr[(l + r) >> 2];
    if (x > y) swap(x, y);
    if (x > z) swap(x, z);
    if (y > z) swap(y, z);
    return y;
}

void quick_sort_v5(int *arr, int l, int r) {
    while (l < r) {
        int x = l, y = r, z = median(arr, l, r);
        do {
            while (arr[x] < z) ++x;
            while (arr[y] > z) --y;
            if (x <= y) {
                swap(arr[x], arr[y]);
                ++x;
                --y;
            }    
        } while (x <= y);
        quick_sort_v5(arr, l, y);
        l = x;
    }
    return;
}       

混合算法

当子序列较短时用插入排序更合适，子序列较长时快速排序性能更优。

void unguarded_insert_sort(int *arr, int l, int r) {
    int min = l;
    for (int i = l + 1;i <= r; i++) {
        if (arr[i] < arr[min]) min = i;
    }
    while (min > l) {
        swap(arr[min], arr[min - 1]);
        --min;
    }
    for (int i = l + 2; i <= r; i++) {
        int j = i;
        if (arr[j] < arr[j - 1]) {
            swap(arr[j], arr[j - 1]);
            j--;
        }
    }
    return;
}

void quick_sort_v6(int *arr, int l, int r) { 
    while (r - l > 16) {
        int x = i, y = r, z = median(arr, l, r);
        do {
            while (arr[x] < z) ++x;
            while (arr[y] > z) --y;
            if (x <= y) {
                swap(arr[x], arr[y]);
                ++x, --y;
            }
        } while (x<= y);
        quick_sort_v5(arr, l ,y);
        l = x;
    }
    if (l < r) {
        unguarded_insert_sort(arr, l, r); 
    }
    return;
}
    

应用： 找出无序数列中的中位数（第N大/小的数）

采用快速排序中的partition部分解题。优点是无需完全排序，中间过程即可得解：

//返回partition完成后基准值的下标
int partition(int *arr, int l, int r) {
    int z = arr[l]; //基准值取最左端
    while (l < r) {
        while (l < r && arr[r] >= z) r--;
        if (l < r) arr[l++] = arr[r];
        while (l < r && arr[l] <= z) ++l;
        if (l < r) arr[r--] = arr[l];
    } 
    arr[l] = z;
    return l;
}
//找出中位数
int find_mid(int *arr, int n) {
    int l = 0, r = n - 1, mid = (n - 1) / 2;
    int num;
    while (1) {
        num = partition(arr, l, r);
        if (mid == num)  break;
        if (mid > num) {
            l = num + 1;
        }
        if (mid < num) {
            r = num - 1;
    }
    return (n & 0x01) ? arr[mid] : (arr[mid] + arr[mid + 1]) / 2;
}

partition优化（C++）：

int partition(int *num, int left, int right) {
    int l = left, r = right;
    while (l < r) {
        while (l < r && num[r] >= num[l]) r--;
        swap(num[l], num[r]);
        while (l < r && num[l] <= num[r]) i++;
        swap(num[l], num[r]);
    }
    return l;
}

【思考：为什么最后返回的一定是left指针指向的位置？】

参考资料：

https://blog.csdn.net/coolwriter/article/details/78732728

https://blog.csdn.net/weixin_41190227/article/details/86600821

https://www.cnblogs.com/itsharehome/p/11058010.html

https://blog.csdn.net/linrulei11/article/details/7983231