割点

割点的概念

在无向连通图中，如果将其中一个点以及所有连接该点的边去掉，图就不再连通，那么这个点就叫做割点（cut vertex / articulation point）。

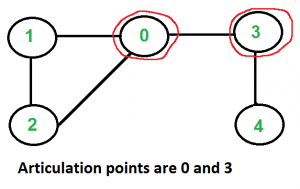
例如，在下图中，0、3是割点，因为将0和3中任意一个去掉之后，图就不再连通。如果去掉0，则图被分成1、2和3、4两个连通分量；如果去掉3，则图被分成0、1、2和4两个连通分量。

Tarjan算法

可以使用Tarjan算法求割点（注意，还有一个求连通分量的算法也叫Tarjan算法，与此算法类似）。（Tarjan，全名Robert Tarjan，美国计算机科学家。）

首先选定一个根节点，从该根节点开始遍历整个图（使用DFS）。

对于根节点，判断是不是割点很简单——计算其子树数量，如果有2棵即以上的子树，就是割点。因为如果去掉这个点，这两棵子树就不能互相到达。

对于非根节点，判断是不是割点就有些麻烦了。我们维护两个数组dfn[]和low[]，dfn[u]表示顶点u第几个被（首次）访问，low[u]表示顶点u及其子树中的点，通过非父子边（回边），能够回溯到的最早的点（dfn最小）的dfn值（但不能通过连接u与其父节点的边）。对于边(u, v)，如果low[v]>=dfn[u]，此时u就是割点。

但这里也出现一个问题：怎么计算low[u]。

假设当前顶点为u，则默认low[u]=dfn[u]，即最早只能回溯到自身。

有一条边(u, v)，如果v未访问过，继续DFS，DFS完之后，low[u]=min(low[u], low[v])；

如果v访问过（且u不是v的父亲），就不需要继续DFS了，一定有dfn[v]<dfn[u]，low[u]=min(low[u], dfn[v])。

Tarjan算法

首先假设u是根节点。如果u有两棵以上的子树，则u为割点。代码：

int children = 0;
for (int v: g[u])
{
    if (!vis[v])
    {
        children++;
        dfs(v);   // 继续DFS
    }
}
if (children >= 2)
    // u是割点

非根节点呢？按照前面的描述，代码如下：

// 默认u不能回溯到任何前面的点
low[u] = dfn[u];
for (int v: g[u])
{
    // (u, v)为树边
    if (!vis[v])
    {
        // 设置v的父亲为u
        parent[v] = u;
        // 继续DFS，遍历u的子树
        dfs(v);
        // u子树遍历完毕，low[v]已求出，low[u]取最小值
        low[u] = min(low[u], low[v]);

        if (low[v] >= dfn[u])
            // u是割点
    }
    // (u, v)为回边，且v不是u的父亲
    else if (v != parent[u])
        low[u] = min(low[u], dfn[v]);
}

综合起来，加上一些其它部分，Tarjan算法的代码如下：

const int V = 20;
int dfn[V], low[V], parent[V];
bool vis[V], ap[V];
vector<int> g[V];

void dfs(int u)
{
    static int count = 0;
    // 子树数量
    int children = 0;

    // 默认low[u]等于dfn[u]
    dfn[u] = low[u] = ++count;
    vis[u] = true;

    // 遍历与u相邻的所有顶点
    for (int v: g[u])
    {
        // (u, v)为树边
        if (!vis[v])
        {
            // 递增子树数量
            children++;
            // 设置v的父亲为u
            parent[v] = u;
            // 继续DFS
            dfs(v);
            // DFS完毕，low[v]已求出，如果low[v]<low[u]则更新low[u]
            low[u] = min(low[u], low[v]);

            // 如果是根节点且有两棵以上的子树则是割点
            if (parent[u] == -1 && children >= 2)
                cout << "Articulation point: " << u << endl;
            // 如果不是根节点且low[v]>=dfn[u]则是割点
            else if (parent[u] != -1 && low[v] >= dfn[u])
                cout << "Articulation point: " << u << endl;
        }
        // (u, v)为回边，且v不是u的父亲
        else if (v != parent[u])
            low[u] = min(low[u], dfn[v]);
    }
}

不过有一个问题：可能会重复输出一个割点。例如一个图里有(1, 2)、(1, 3)、(1, 4)和(1, 5)四条边（取1为根节点），发现(1, 3)时就已经输出了1，但发现(1, 4)和(1, 5)时就又输出了两遍。所以需要使用一个数组ap[]来记录割点。

还有一个可以优化的地方：我们使用vis[]来记录一个点是否访问过。但是我们想一下，不是只有访问过的点才会分配dfn吗？当然，没有访问过的顶点，dfn[]里也有值，但这里dfn[]是全局的，因此它的每个元素最初都是0。因此完全可以取消vis[]数组并把!vis[v]改成!dfn[v]。

最后一个点：下面的代码：

if (parent[u] == -1 && children >= 2)
    cout << "Articulation point: " << u << endl;
else if (parent[u] != -1 && low[v] >= dfn[u])
    cout << "Articulation point: " << u << endl;

可以合起来写成：

if (parent[u] == -1 && children >= 2 || parent[u] != -1 && low[v] >= dfn[u])
    cout << "Articulation point: " << u << endl;

对Tarjan算法的详细理解

首先，“根节点有n棵子树”这句话，是说这n棵子树是独立的，没有根节点不能互相到达。因此n不一定等于与根节点相邻的顶点数。因此加入了vis[v]为false的条件，因为如果(u, v1)和(u, v2)在一棵子树里，对v1进行DFS，一定能去到v2，vis[v2]就会为true，此时就不会children++了。

对于边(u, v)，如果low[v]>=dfn[u]，即v即其子树能够（通过非父子边）回溯到的最早的点，最早也只能是u，要到u前面就需要u的回边或u的父子边。也就是说这时如果把u去掉，u的回边和父子边都会消失，那么v最早能够回溯到的最早的点，已经到了u后面，无法到达u前面的顶点了，此时u就是割点。