数据:14天打球情况
特征:4种环境变化,outlook观察,temperature温度,humidity湿度,windy刮风
目标:构造决策树

根据四种特征决策play
划分方式:4种
问题:谁当根节点呢?
依据:信息增益

在历史数据中(14天)有9天打球,5天不打球,所以此时的熵应为:
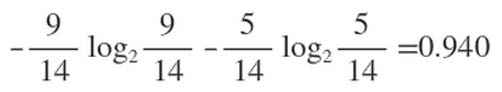
关于log的底,选取什么都可以,但是要统一
4个特征逐一分析,先从outlook特征开始:

Outlook = sunny时,熵值为0.971
$-frac{2}{5} imes log_{2}frac{2}{5}-frac{3}{5} imes log_{2}frac{3}{5}$
Outlook = overcast时,熵值为0
$-frac{4}{4} imes log_{2}frac{4}{4}-frac{0}{4} imes log_{2}frac{0}{4}$
Outlook = rainy时,熵值为0.971
$-frac{3}{5} imes log_{2}frac{3}{5}-frac{2}{5} imes log_{2}frac{2}{5}$
根据数据统计,outlook取值分别为sunny,overcast,rainy的概率分别为:5/14, 4/14, 5/14,sunny占14天中的5天,以此类推
熵值计算:5/14 * 0.971 + 4/14 * 0 + 5/14 * 0.971 = 0.693
信息增益:系统的熵值从原始的0.940下降到了0.693,增益为0.247
其他信息增益:
(gain(temperature)=0.029 gain(humidity)=0.152 gain(windy)=0.048)
同样的方式可以计算出其他特征的信息增益,那么我们选择最大的那个就可以啦,相当于是遍历了一遍特征,找出来了大当家,然后再其余的中继续通过信息增益找二当家!
ID3:信息增益(有什么问题呢?)每个ID之出现一次,所以算出来的信息增益会很大
C4.5:信息增益率(解决ID3问题,考虑自身熵)信息增益比上自身的熵值
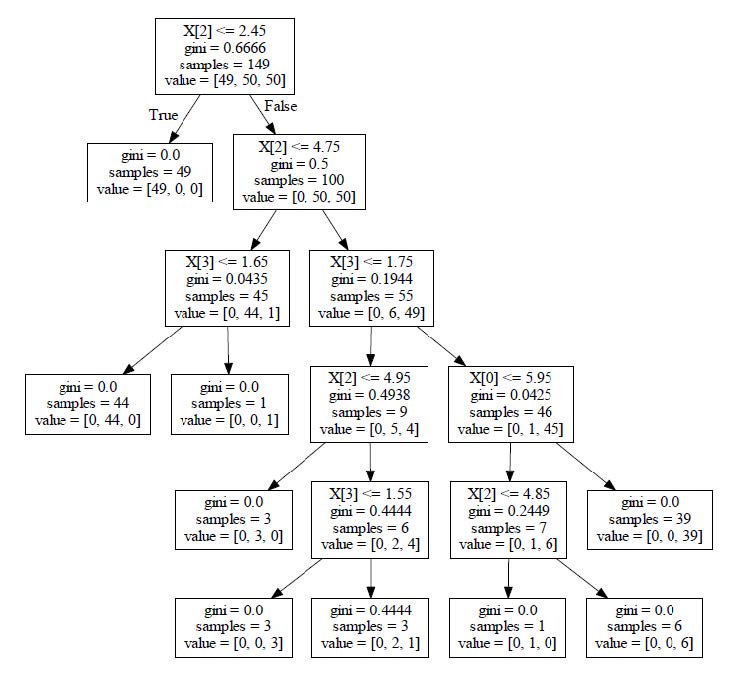
CART:使用GINI系数来当做衡量标准
GINI系数:

(和熵的衡量标准类似,计算方式不相同)
连续值怎么办?

决策树剪枝策略
为什么要剪枝:决策树过拟合风险很大,理论上可以完全分得开数据(想象一下,如果树足够庞大,每个叶子节点不就一个数据了嘛)
剪枝策略:预剪枝,后剪枝
预剪枝:边建立决策树边进行剪枝的操作(更实用)
后剪枝:当建立完决策树后来进行剪枝操作
预剪枝:限制深度,叶子节点个数叶子节点样本数,信息增益量等
后剪枝:通过一定的衡量标准

(叶子节点越多,损失越大)
C(T) = gini*samples,α = 系数,Tleaf = 叶子节点数