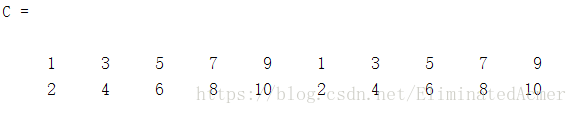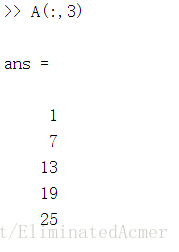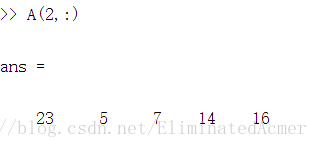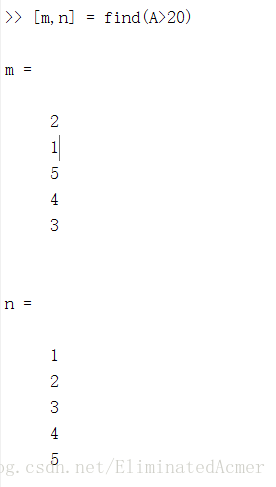一、矩阵的定义与构造
(1)生成一个3*3的矩阵
A = [1,4,2;3,5,6;7,2,8]
(2)得到A矩阵的转置
B = A'
(3)将此矩阵转化为列向量(按照列的形式)
C = A(:)
(4)计算矩阵A的逆,并利用 A * D 测试,会得到一个单位矩阵
D = inv(A)
(5)生成三维矩阵(使用 zeros() 或 ones() 函数,zeros() 生成全 0 矩阵,ones()生成全 1 矩阵)
A = zeros(3,3,3)
前两个参数指定每个矩阵的维度,最后一个决定包含多少个矩阵,例如
A = zeros(3,3,4)
三维矩阵一般用于图像信息的存储,例如
A(:,:,1) = rand(3,3);A(:,:,2) = randi([0,10],3,3);A(:,:,3) = randn(3,3)
分别给三个二维矩阵赋值,其中,rand 生成均匀分布的伪随机数。分布在(0~1)之间,randi 生成均匀分布的伪随机整数, randn 生成标准正态分布的伪随机数(均值为0,方差为1),它们三个语法如下:
① rand(m,n)生成m行n列的均匀分布的伪随机数,rand(m,n,'double')生成指定精度的均匀分布的伪随机数
② randi(iMax)在开区间(0,iMax)生成均匀分布的伪随机整数,randi(iMax,m,n)在开区间(0,iMax)生成mXn型随机矩阵,r = randi([iMin,iMax],m,n)在开区间(iMin,iMax)生成mXn型随机矩阵
③ randn(m,n)生成m行n列的均匀分布的伪随机数,randn(m,n,'double') 生成指定精度的均匀分布的伪随机数
效果如下:
(6)利用 cell() 生成元胞数组
A = cell(1,4)
它与矩阵的不同之处是内部矩阵可以不同维
A{2} = eye(3);A{4} = magic(4)eye(n) 函数生成一个 n*n 单位矩阵,magic(n) 函数生成一个 n*n 的矩阵,矩阵元素由 1 ~ n^2 组成,且任何行任何列的和都相等。
(7)对于有规律的矩阵可以这样定义
A = 1:2:9这个语句的意思是矩阵元素值从 1 ~ 9 ,以 2 为间隔
如果要复制矩阵 A ,使用 repmat() 函数
C = repmat(A,3,1)复制矩阵A,并且形成 3 行 1 列
2*2 矩阵
A = [1:2:9;2:2:10]
复制矩阵A
C = repmat(A,1,2)2.矩阵的四则运算
(1)定义两个矩阵
A = [1,2,3,4;5,6,7,8];B = [8,7,6,5;4,3,2,1]+ 和 - 就不多说了,主要列举如下运算,* 和 .*
对于 * 运算,两个矩阵必须满足左边矩阵的列数等于右边矩阵的行数,而 .* 运算,即对应元素相乘,两个矩阵必须满足规格相 同,类似的, / 运算性质与其相似。
3.矩阵的下标
(1)现在存在这样一个矩阵
(2)得到某个确定元素
(3)得到某一列元素
(4)得到某一行元素
(5)获得满足某一条件的元素下标