D.坏掉的手表
时间限制: 1 Sec 内存限制: 128 MB
[提交] [状态]
题目描述
有个手表坏了,时间为HH:MM,你要把这个不合法的时间变为合法,请求出最少要动几位
输入
第一行表示手表时间是什么制式
第二行HH:MM表示手表当前时间
输出
一个整数表示答案
样例输入 Copy
12
17:30
样例输出 Copy
1
题意:
给定时间制和时间,问最少变几位使得该时间符合时间制。
思路:
模拟模拟模拟
但这个题巨坑啊。
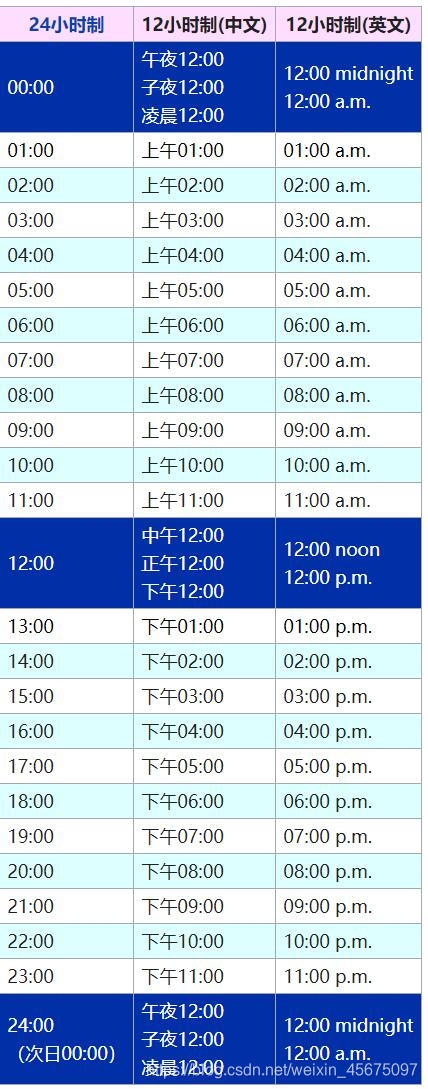
奇奇怪怪的数据比如说:12小时制的12:50是合法的。其他就看看下面的图就好了。
代码:
队友写的直接贴过来了
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<queue>
#include<stack>
#include<map>
using namespace std;
const long long inf =0x3f3f3f3f;
const int maxn=1e6+5;
const long long mod =19260817;
#define PI 3.14159265358979323846
#define ll long long
#define ull unflaged ll
inline int read()
{
int x=0,f=1;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s<='9'&&s>='0'){x=x*10+s-'0';s=getchar();}
return x*f;
}
string s;
int main()
{
int n;
cin>>n;//n制式
cin>>s;
int ans=0;
int t1=((s[0]-'0')*10)+(s[1]-'0');
int t2=((s[3]-'0')*10)+(s[4]-'0');
if(n==12)
{
if(t1>n||t1<1) ans++;
if(t2>=60) ans++;
}
else
{
if(t1>=n) ans++;
if(t2>=60) ans++;
}
cout<<ans<<endl;
}
E.流星
时间限制: 1 Sec 内存限制: 128 MB
[提交] [状态]
题目描述
我带着深藏骨血的仇恨与酝酿多年的阴谋
把自己变成一个死而复生的幽灵沉入沼泽,沉入深渊
我想埋下腐烂的根系长出见血封喉的荆棘刺穿这个虚伪的文明
我到了淤泥深处……捡到了一颗星星。
晨光起于白塔尖顶,终将铺满阴霾之地。
Marser正在和副词看星星。这时,他们发现了一颗流星划过天际。Marser出于习惯,记录下了这颗流星出现和消失的位置。Marser两组坐标来描述这两个位置。你可以认为它们被Marser放在了一个原点由Marser指定的笛卡尔坐标系中。
现在,副词为了考验Marser的智商,想问他一个问题:按照Marser的坐标系定义,这颗流星一共经过了多少个格点?这里,格点被定义为坐标均为整数的点。
Marser用了1ms就完成了这个问题,于是他想用这个问题来测试您的智力。当然,为了简化您的操作,您可以把流星的运动轨迹看成一条直线。这样,您可以把这个问题转化为求一条线段除了端点外经过了多少个格点。
输入
读入两行,每行两个整数 x,y,表示线段的两个端点的坐标。
输出
输出一行一个整数,表示除了两个端点外,线段经过的格点数量。
样例输入 Copy
1 11
5 3
样例输出 Copy
3
提示
对于30%的数据,保证max(∣x∣,∣y∣)≤103;
对于60%的数据,保证max(∣x∣,∣y∣)≤106;
对于全部数据,保证max(∣x∣,∣y∣)≤1012。
题意:
求除了两个端点外,线段经过的格点数量。
思路:
GCD的性质。以前做过加强版。
博客讲解
需要注意:
1.开long long
2.当线段的两个端点重合时需要特判
代码:
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
ll gcd(ll a,ll b){
return b==0?a:gcd(b,a%b);
}
void AC(){
ll x1,y1,x2,y2;
scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
ll res;
if(x1==x2&&y1==y2) res=0;
else{
ll xx=abs(x1-x2),yy=abs(y1-y2);
ll GCD=gcd(xx,yy);
res=GCD-1;
}
printf("%lld
",res);
}
int main(){
AC();
return 0;
}
F: Hash 键值
时间限制: 1 Sec 内存限制: 128 MB
[提交] [状态]
题目描述
所有的苦难与背负尽头,
都是行云流水般的此世光阴。
一生所渴求的,全都伤人至深。
而一生所憎恶的,全都令人魂牵梦萦。
Marser 沉迷 hash无法自拔,然而他发现自己记不住 hash 键值了……
Marser 使用的 hash 函数是一个单纯的取模运算,每一个数 i 被对应到 i mod p。他现在有一个数列 a1,a2,…,an,他采用这种方法,把每一个数 ai 对应到一个键值 i mod p。他想知道对于给定的模数 p 和键值 r,所有对应到该键值的数的和为多少。同时,Marser 可能会发现他的数列出了一些问题,所以他还想随时更改数列中任意一项的值。
现在 Marser 有 q 个请求,每个请求可能是修改或是询问。对于每一个询问,你需要给出正确的答案。如果你不能在 1s 内正确回答所有询问,Marser 就会让 hotwords 把你给续了。
输入
第一行两个整数 n,q,表示数列长度和请求数量。
第二行 n 个整数,表示初始的序列。
接下来 q 行,每行三个整数 opt,x,y;
若 opt=1,则询问在 mod x 时,所有对应到键值 y 的数的和。
若 opt=2,则将数列第 x 项修改为 y。
输出
对于每个询问,输出相应的答案。
样例输入 Copy
10 5
1 2 3 4 5 6 7 8 9 10
1 2 1
2 1 20
1 3 1
2 5 1
1 5 0
样例输出 Copy
25
41
11
提示
对于 100% 的数据,保证 n,q≤105,输出的所有数据在 int 范围内。
思路源于:传送门
有被惊艳到。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+100;
ll s[2100][2100];
ll a[maxn];
int n,q;
void AC(){
scanf("%d%d",&n,&q);
int block=sqrt(n);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
for(int j=1;j<=block;j++)
s[j][i%j]+=a[i];
}
while(q--){
int op,x,y;
scanf("%d%d%d",&op,&x,&y);
if(op==1){
if(x<=block) printf("%lld
",s[x][y]);
else{
ll res=0;
for(int i=y;i<=n;i+=x) res+=a[i];
printf("%lld
",res);
}
}
else{
///先更新区间
for(int i=1;i<=block;i++)
s[i][x%i]=s[i][x%i]-a[x]+y;
///再更新单点
a[x]=y;
}
}
}
int main(){
AC();
return 0;
}
G: 麦田
时间限制: 1 Sec 内存限制: 128 MB
[提交] [状态]
题目描述
我心里有一簇迎着烈日而生的花,
比一切美酒都要芬芳,
滚烫的馨香淹没过稻草人的胸膛,
草扎的精神,从此万寿无疆。
凝视深渊的人,深渊也在凝视你。
我不是凝视深渊的人,我就是深渊。
Marser 来到了一片麦田。他想穿过这片麦田,去找副词一起学习。
但是,他发现这片麦田有一些特殊的性质。我们可以把麦田抽象成一片 n×mn imes mn×m 的网格,每个格子上都有一个数字。同时,Marser 按如下的方式表示前进的方向:
如果往与所在格子上数字相同的方向前进,Marser 不需要花费体力;而往其他方向前进时,Marser 就需要额外花费 111 单位的体力。
现在,Marser 想知道,从给定的起点前进到给定的终点,最少需要消耗多少体力?
输入
第一行两个整数 n,m(n,m≤1000),表示麦田的大小。
接下来 n 行,每行一个长度为 m 的字符串,表示每个格子上的数字。
接下来一行,四个整数 xs,ys,xt,yt,表示起点和终点的位置。
输出
输出一行一个整数,表示最少需要消耗的体力。
样例输入 Copy
5 5
04125
03355
64734
72377
02062
4 2 4 2
样例输出 Copy
0
题意:
每个点可以向周围8个方向走,如果走的格子的数字和当前方位代表的数字相同,花费就是0,否则花费就是1,问最小花费。
思路:
花费不是0就是1,双端队列BFS裸题。
博客讲解
注意输入的形式,可以用字符串类型输入,也可以用
scanf("%1d",&g[i][j]);
输入,表示逐位输入。
代码:
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
#define x first
#define y second
typedef pair<int,int>PII;
int g[1100][1100];
int n,m;
int sx,sy,ex,ey;
int res=0;
int nx[8]={-1,-1,0,1,1,1,0,-1};
int ny[8]={0,1,1,1,0,-1,-1,-1};
int dis[1100][1100];
bool st[1100][1100];
void bfs(){
memset(dis,0x3f,sizeof dis);
memset(st,0,sizeof st);
dis[sx][sy]=0;
deque<PII>q;
q.push_back({sx,sy});
while(q.size()){
PII t=q.front();
q.pop_front();
if(t.x==ex&&t.y==ey) break;
st[t.x][t.y]=1;
for(int i=0;i<8;i++){
int a=t.x+nx[i],b=t.y+ny[i];
if(a<1||a>n||b<1||b>m) continue;
if(dis[a][b]>dis[t.x][t.y]+(g[t.x][t.y]!=i)){
dis[a][b]=dis[t.x][t.y]+(g[t.x][t.y]!=i);
if(g[t.x][t.y]!=i){
///权值为1
///加到队尾
q.push_back({a,b});
}
else{
///权值为0
///加到队首
q.push_front({a,b});
}
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%1d",&g[i][j]);
scanf("%d%d%d%d",&sx,&sy,&ex,&ey);
/* for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
cout<<g[i][j];
if(j==m) puts("");
else cout<<" ";
}*/
bfs();
printf("%d
",dis[ex][ey]);
return 0;
}