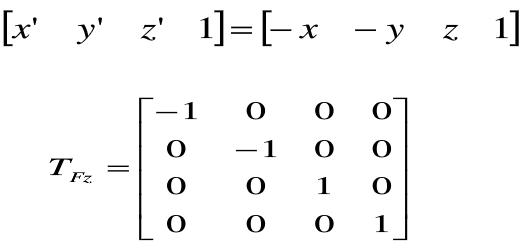三维图形几何变换
一、三维物体基本几何变换
从应用角度看,三维空间几何变换直接与显示、造型有关,因此更重要。
与二维变换类似,引入齐次坐标表示,即:三维空间中某点的变换可以表示成点的齐次坐标与【四】阶的三维变换矩阵相乘。
1、平移变换
若三维物体沿x,y,z方向上移动一个位置,而物体的大小与形状均不变,则称为平移变换。
点P的平移变换矩阵表示如下: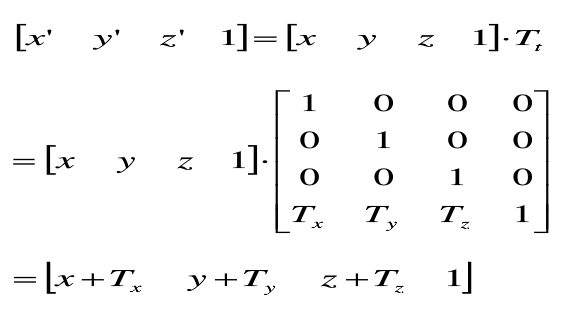
2、比例变换
(1)局部比例变换
局部比例变换由T2D中主对角线元素决定,其它元素均为零。当对x,y,z方向分别进行比例变换时,其变换矩阵表示为:
eg:对下图长方体进行比例变换,a=1/2,e=1/3,i=1/2,求变换后的长方体各点坐标。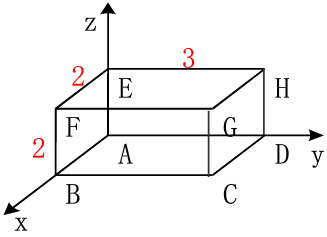
将其写为矩阵计算形式如下: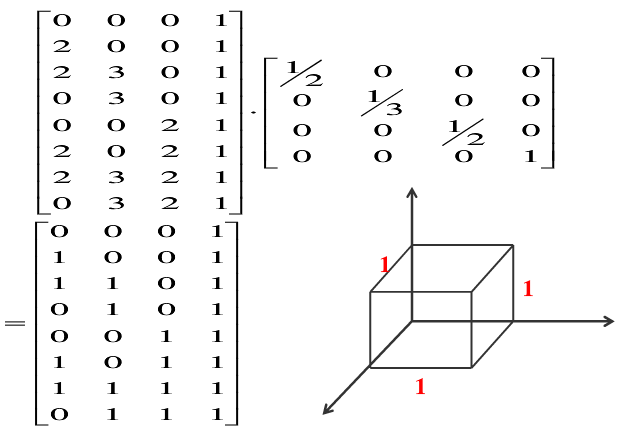
(2)整体比例变换
可以用以下矩阵表示: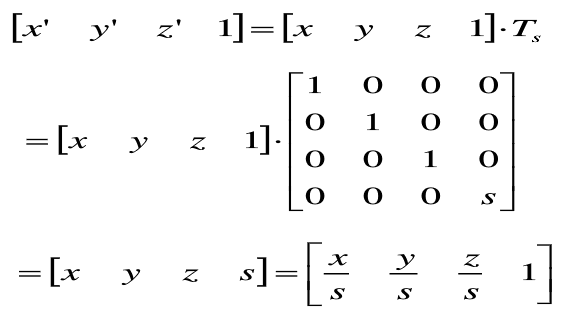
3、旋转变换
三维立体的旋转变换是指给定的三维立体绕三维空间某个制定的坐标轴旋转θ角度,旋转后,立体的【空间位置将发生变化】,但【形状不变】。θ角的正负按右手规则确定,【右手大拇指】指向旋转轴的【正方向】,其余四个手指指向旋转角的【正方向】。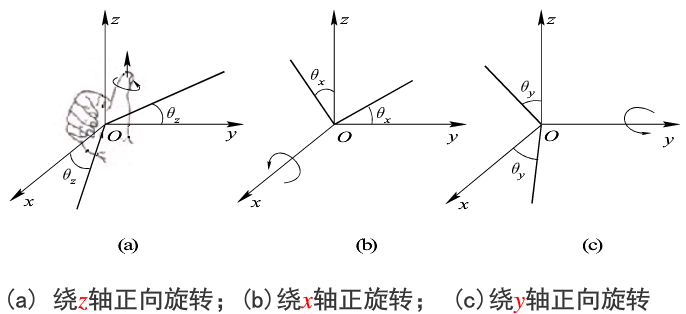
(1)绕z轴旋转θ
可知,绕z轴正方向旋转,x,y坐标改变,而z坐标不变。而x,y坐标可由二维点绕原点旋转公式得到: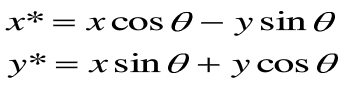
齐次坐标的计算形式为: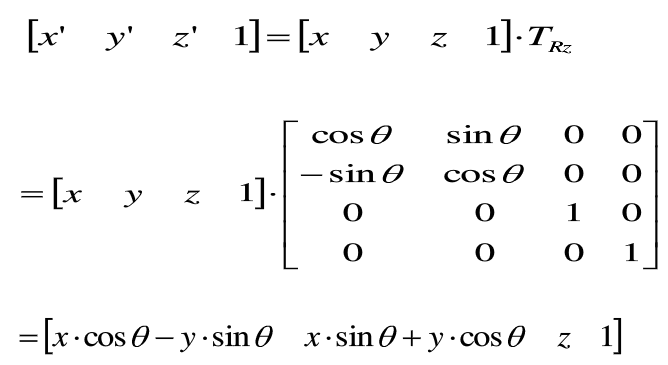
(2)绕x轴旋转
同理可知,齐次坐标的计算形式为: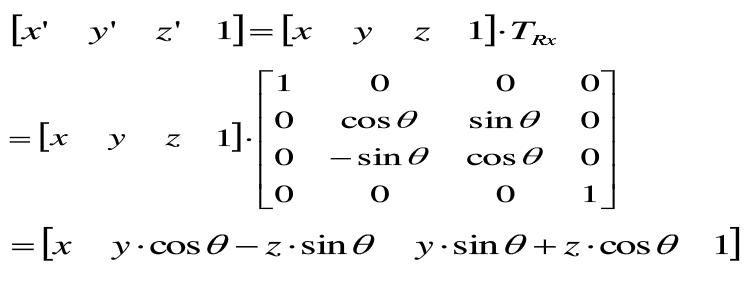
(3)绕y轴旋转
同理可知,齐次坐标的计算形式为: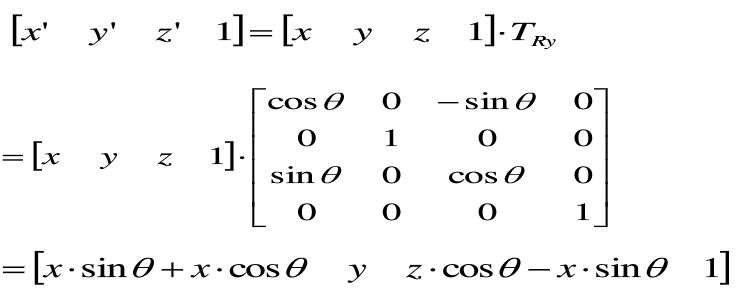
(4)绕任意轴旋转
求任意直线旋转矩阵的原则:
1>任意变换的问题——基本几何变换的问题
2>绕任意直线旋转的问题——绕坐标轴旋转的问题
4、对称变换
(1)关于坐标平面的对称
关于xoy平面进行对称变换[x' y' z' 1]=[x y -z 1]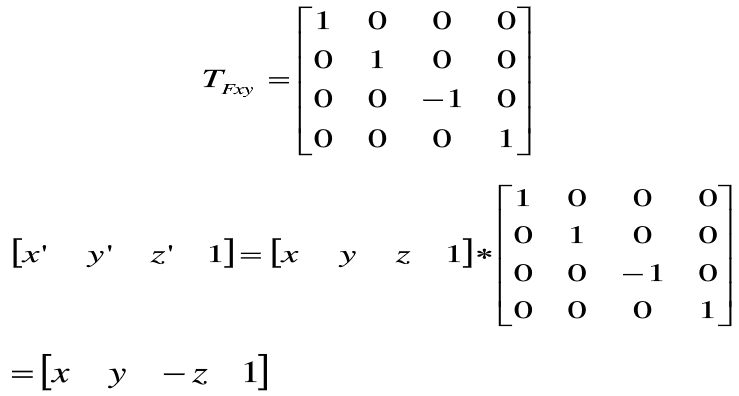
关于yoz平面进行对称变换[x' y' z' 1]=[-x y z 1]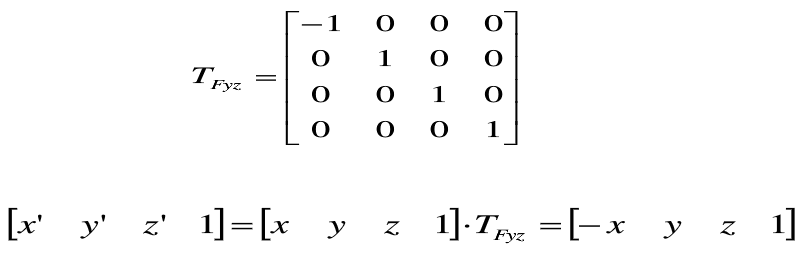
关于zox平面进行对称变换[x' y' z' 1]=[x -y z 1]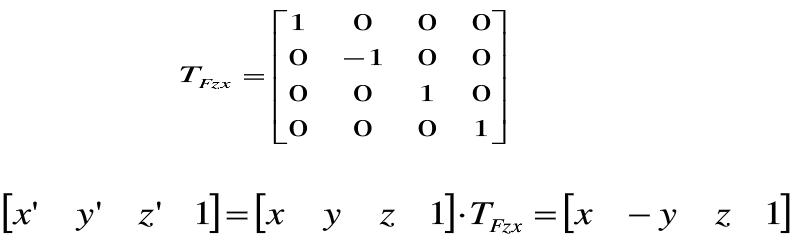
(2)关于坐标轴对称
关于x轴进行对称变换的矩阵计算形式为:
关于y轴进行对称变换的矩阵计算形式为: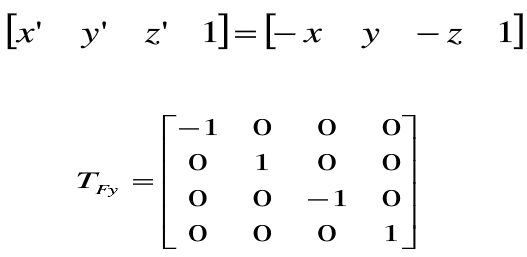
关于z轴进行对称变换的矩阵计算形式为: