题目大意:在n*n的棋盘中,放置n个皇后(同一行、同一列、同一斜线,只有一个皇后)
这道题是一道非常经典的dfs模板题,同一行、同一列的判断不是很难,但同一斜线有一定的难度,下面给出关于斜线编号的解决方法
我们就先以4*4的棋盘为例
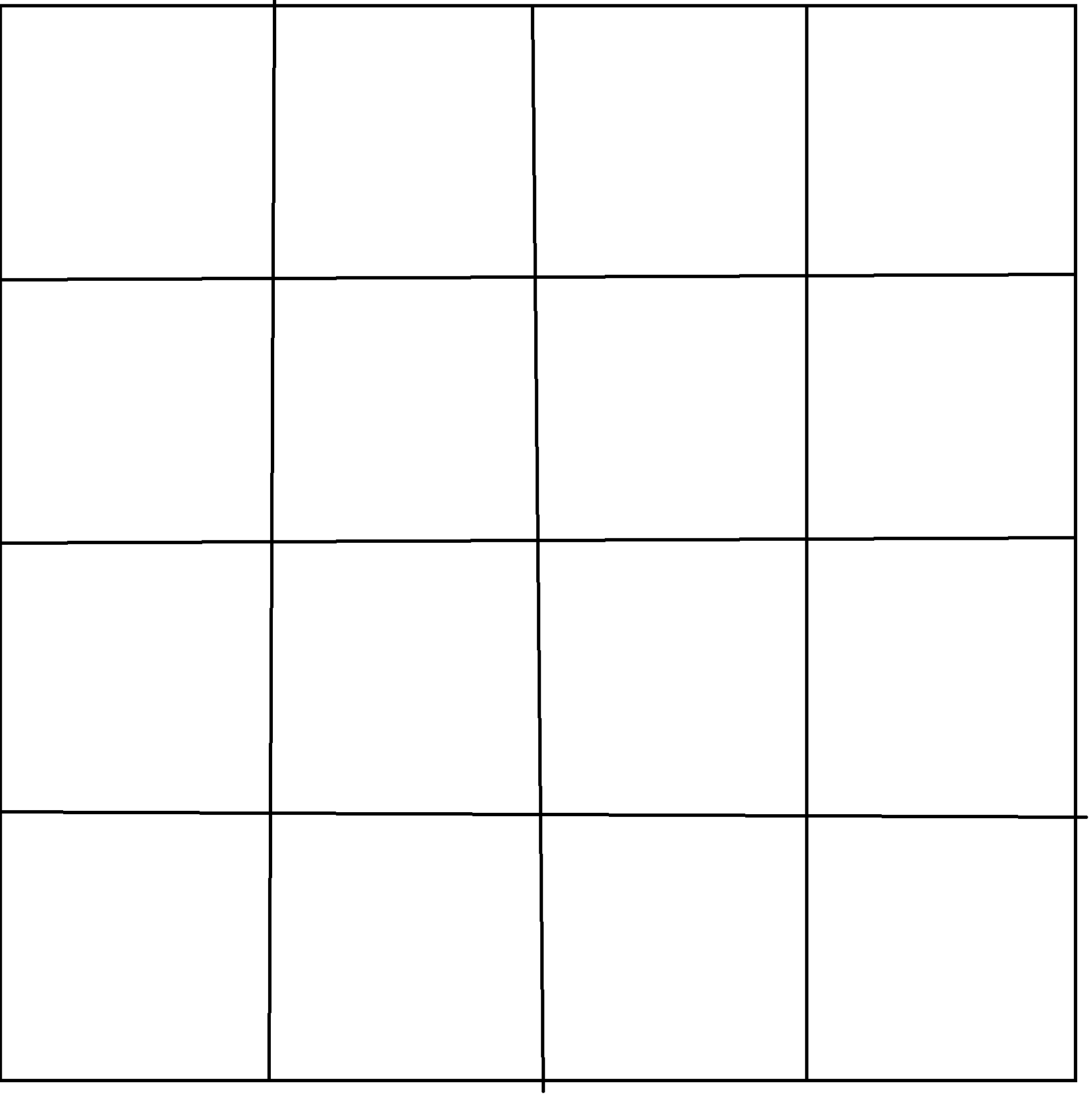
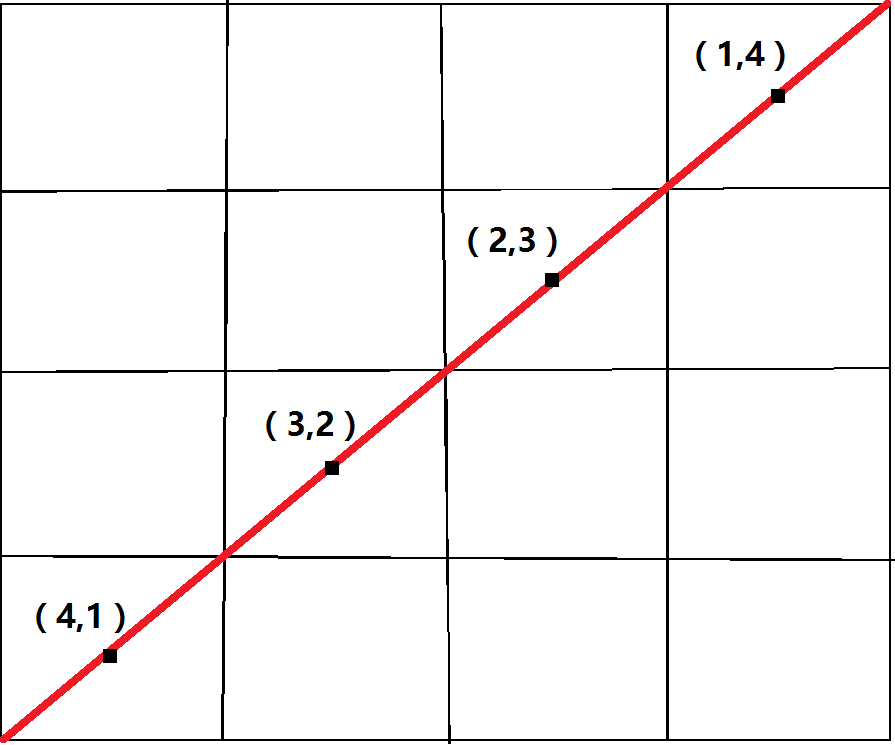
我们把被标红的这一条暂且称之为主对角线
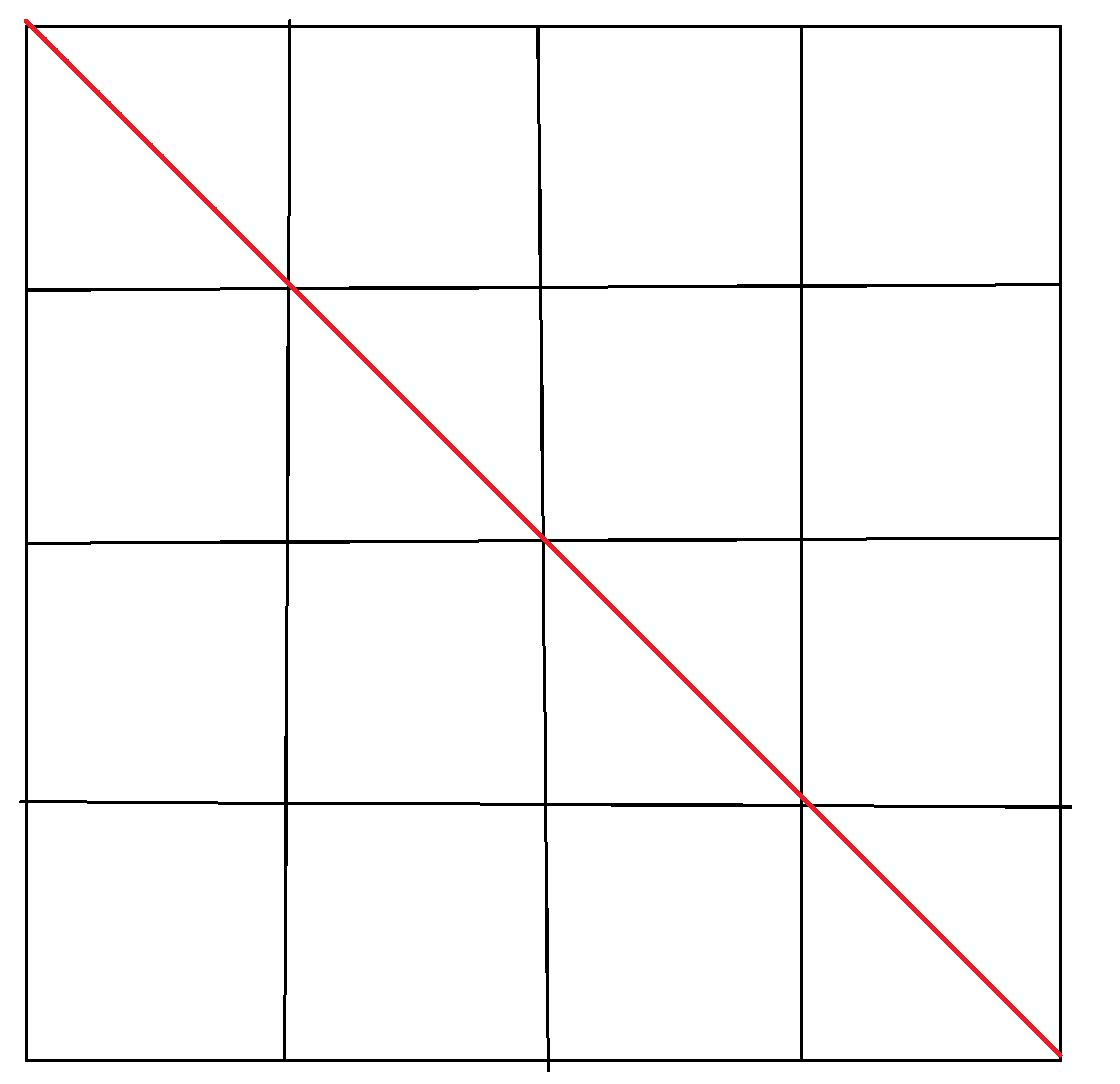
观察一下主对角线上的点坐标规律
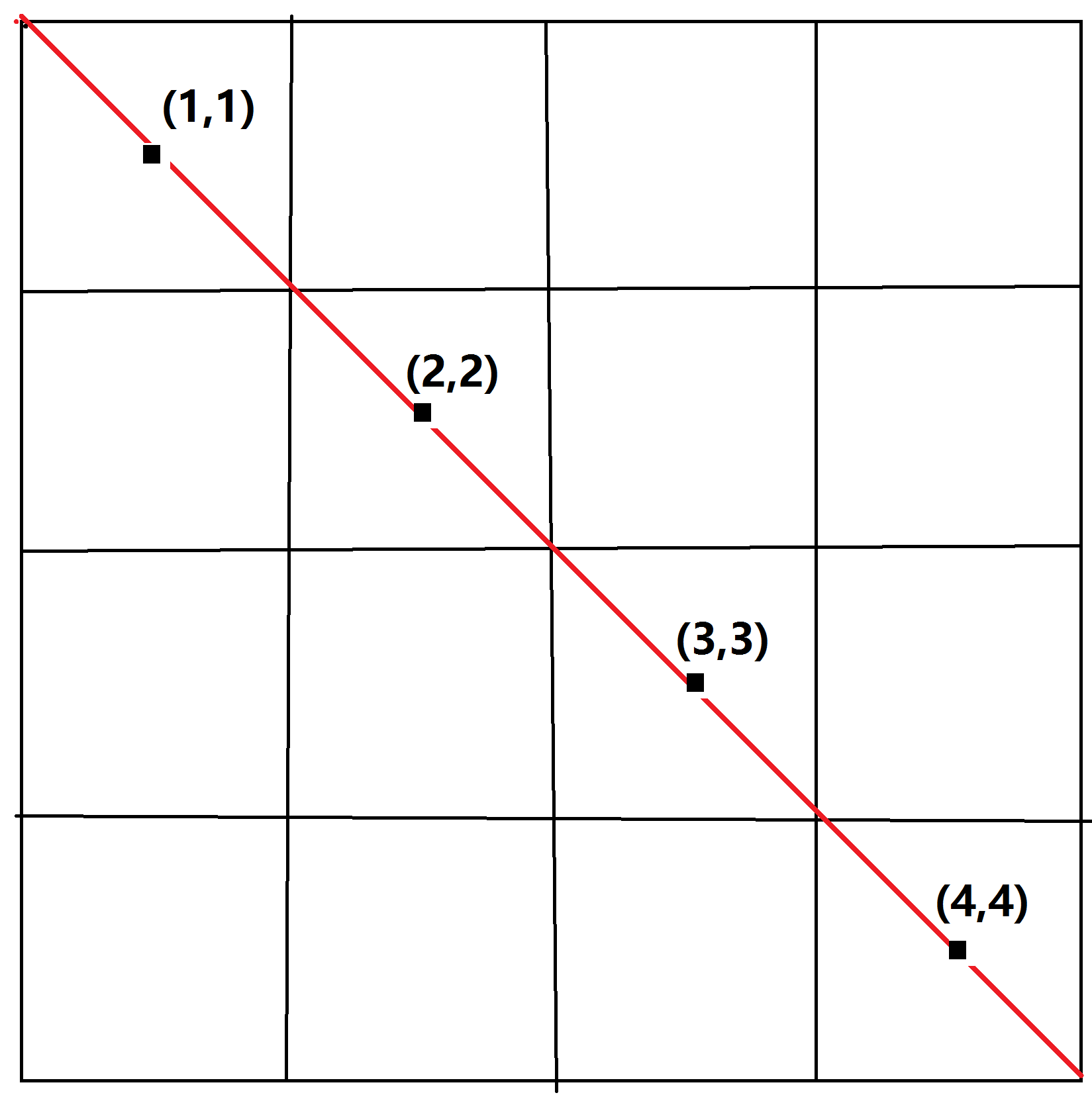
我们发现主对角线上的点的坐标(x,y)满足x==y
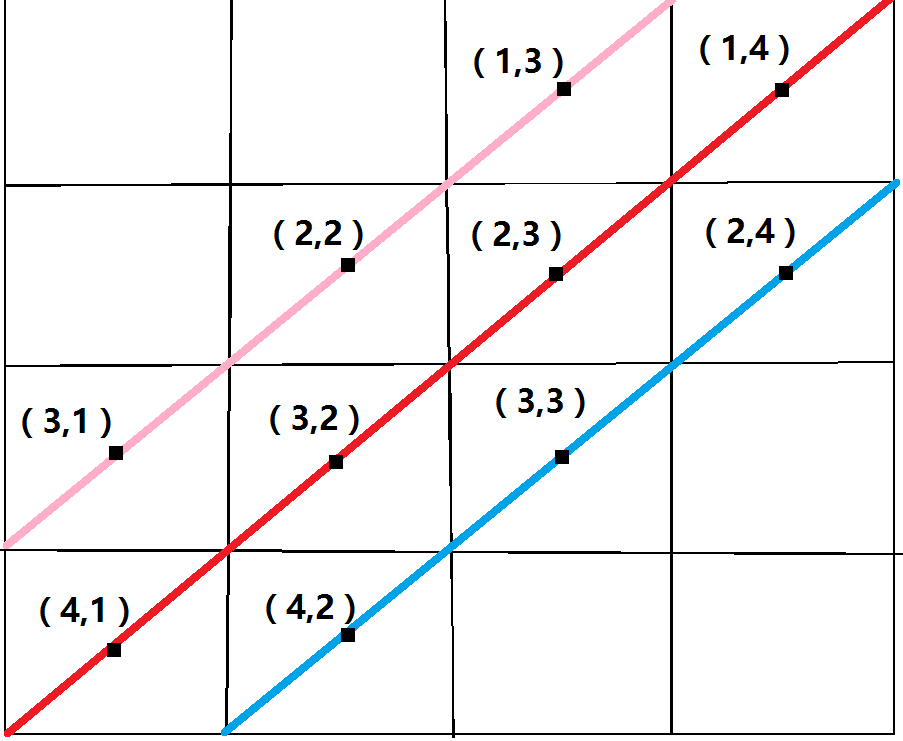
下面看看其他的斜线有怎样的性质
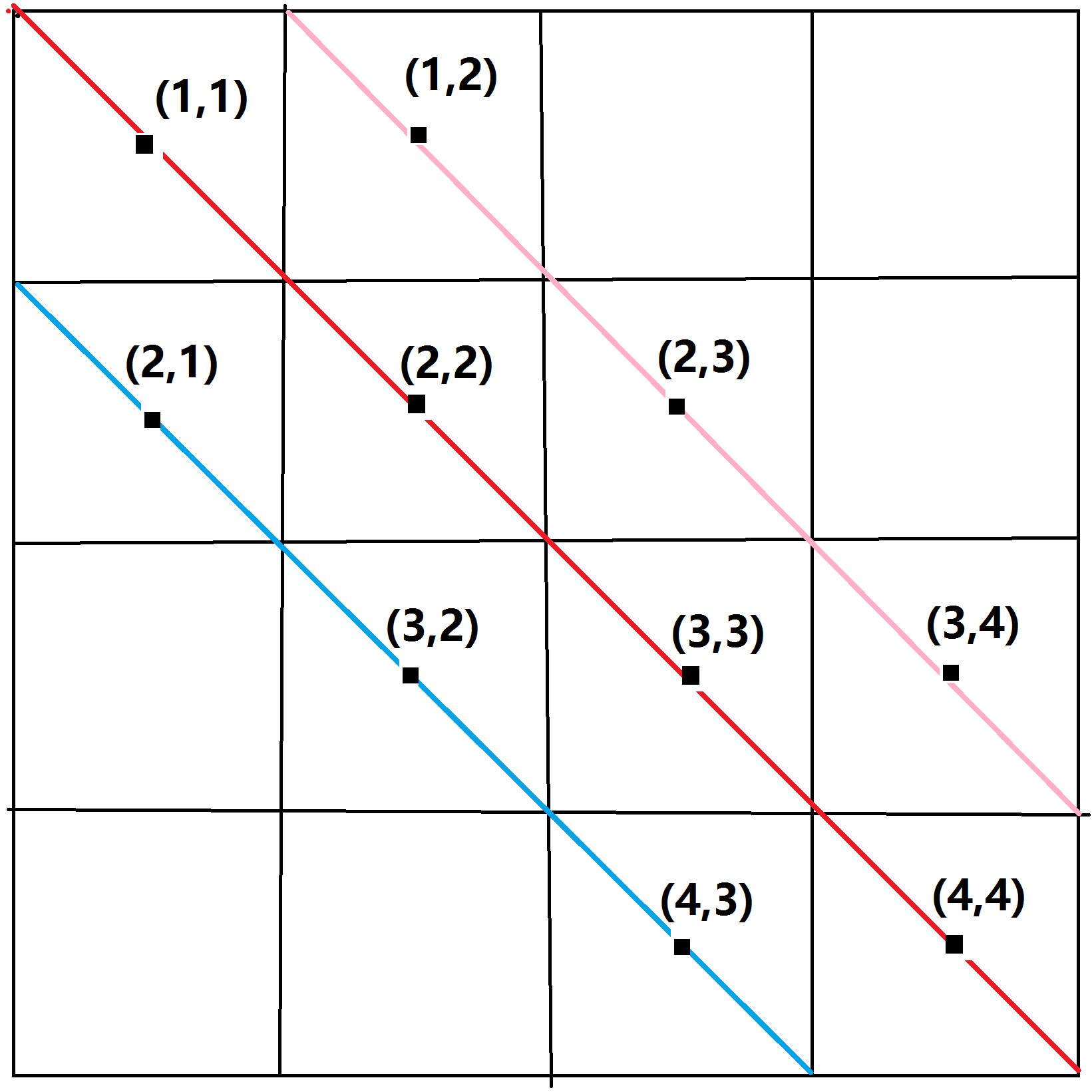
在蓝色这条斜线上的坐标(x,y)满足x-y==1
在粉色这条斜线上的坐标(x,y)满足x-y==-1
同样的,我们也可以吧主对角线的坐标(x,y)表示为x-y==0
所以可以用x-y来计算斜线的编号
x-y的值是从(-4+1)~(4-1)
但是数组下标(在c++)没有负数,所以我们把x-y+n当做数组下标,编号从1~(2*4-1)
同样的,对于n*n的棋盘,共有2n+1条左斜线,我们可以把向左倾斜的斜线编号为(x-y+n)
下面来解决一下向右倾斜的斜线编号(还是以4*4的棋盘为例)
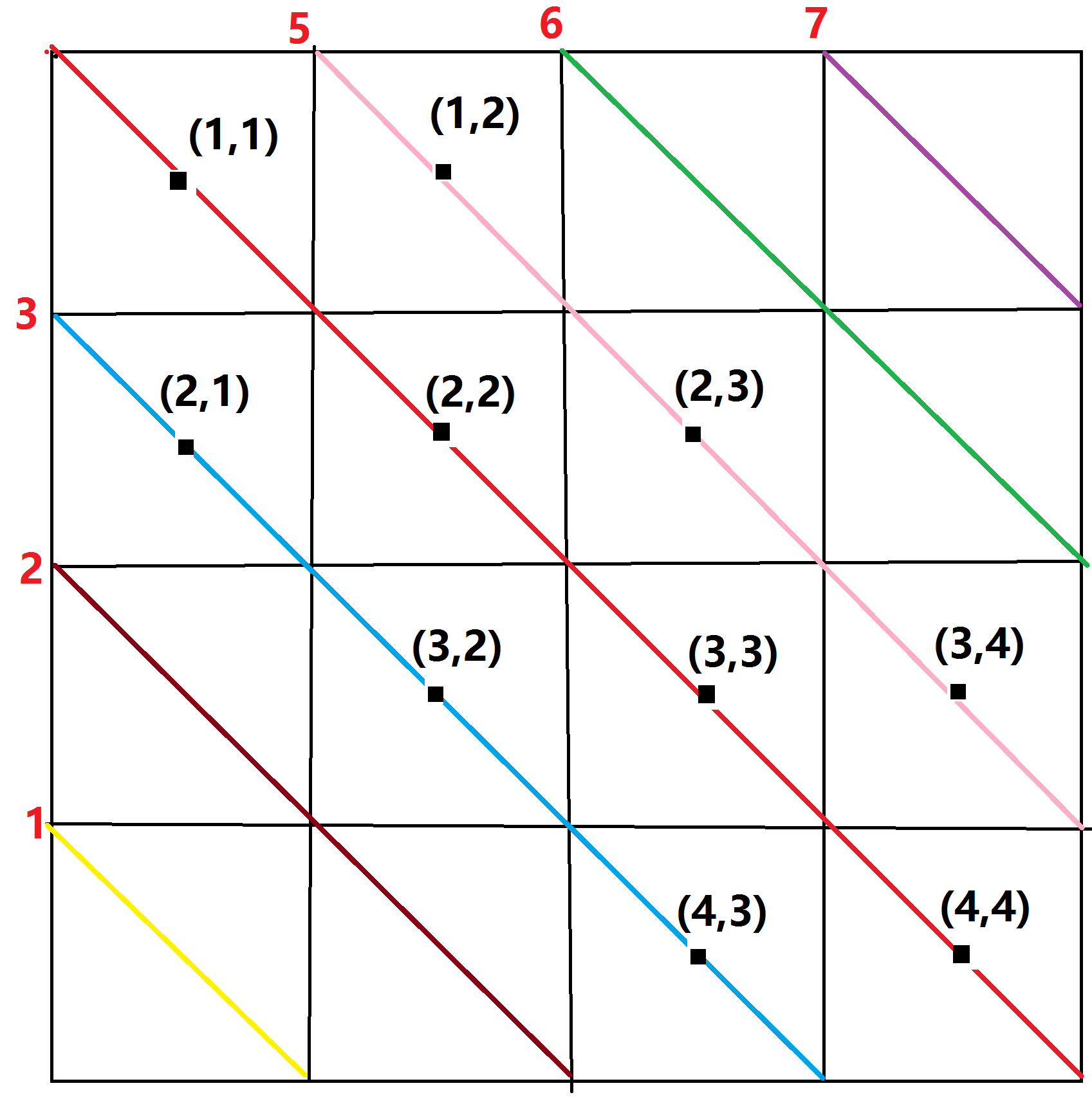
不难看出,在标红的这条向右倾斜的主对角线上点的坐标满足x+y==5
在粉色的这条斜线上x+y==4
在蓝色的这条斜线上x+y==6
同样的,向右倾斜的斜线共有(2*4-1)条,按照x+y来编号,编号为2~8,因为我们普遍采用从1开始的数组下标
所以我们用(x+y-1)当做数组下标,范围是1~7
同样的,对于n*n的棋盘,共有2n+1条右斜线,我们可以把向右倾斜的斜线标号为(x+y-1)