n条直线最多把一个平面拆成1+(n+1)*n/2个区域,
请问:n个平面最多把一个空间拆成多少个区域?(n>=0)
这个问题我想了挺久,后来有在网上搜,并且也搜到了很详细的解答,但是没有看,我还是希望能自己想出来(其实是觉得看那
么多字很烦:-P)。终于在一个漆黑的夜晚灵光一现,地球爆炸了。:)
答案是什么并不重要,重要的是过程。
首先来看n条直线最多能把一个平面拆成多少个区域这个问题。
这个二维的问题是很形象很直观的,我们可以数出来。
直线数 平面区域数
1 2
2 4
3 7
4 11
5 16
6条就比较难数了,不过从前5条对应的平面区域数能很容易看出来这是个一阶等差数列,很容易就能推导出题目中给的公式了。
那么,n个平面拆空间的数目也可以这样数吗?
很遗憾的是,本人三维空间的想象力似乎比二维差很多,四个平面的时候还能凑合着数出来,5个的时候就彻底晕菜了,而仅仅
从前四个数据找规律是很不妥当的,况且规律并不像上面的问题那么轻易就能用眼睛看出来。
于是我又重新回顾直线分平面的过程,用更理性的方法分析我是怎样得到的结果,而不是凭空想象。
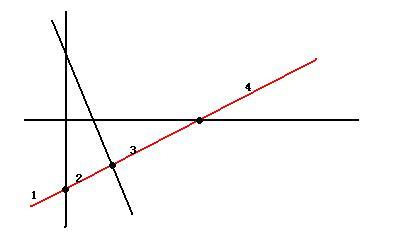
如图
当我们知道了3条直线能把平面分成7个区域的时候,添加第4条直线,那么这条直线必须和另外3条直线都相交才能得到“最多”
把平面分成多少个区域。于是,这3个交点把这条直线分成了4部分,或是线段或是射线,每一部分都将原有的整块区域分成了两
块区域,则新增了4个区域,新增的区域数与直线被分成了几段有关。也就是说,如果我们用a(3)来表示3条直线能分平面的区
域数,a(4)就等于a(3)+4。同理,a(5) = a(4)+5,an = a(n-1)+n = a(n-2)+(n-1)+n = …… = a(1)+2+3+4+
……+n = (n+1)×n/2+1。
那,当我们知道n个平面把空间分成多少区域的时候,能不能推出n+1个平面的情况呢?(忽然觉得这好像数学归纳法哎)
我们来看添加第4个平面的情况。
3个平面分多少区域的问题好象是小学某一年暑假园地的题目:-P,三刀最多能把西瓜切成几块,很简单,8块。
添加第4个平面,这个平面要与其余3个平面都相交,而且不能三个平面交于同一条直线,才能得到“最多”把空间分成多少区域
。所以,第4个平面应该和前3个平面构成一个四面体(三棱锥)。那么,这是多少区域呢?。。似乎有点难数,虽然努力一下可
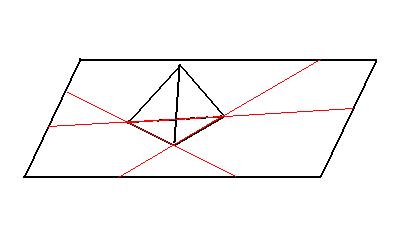
以数出来,但是没有必要。我们来看这个图。
假设四面体的底面是我们新添的平面,图中给出了前3个平面与这个平面的交线。这些交线把这个平面分成了几个部分呢?
咦?这个问题怎么好像做过?
就是3条直线最多把平面分成几个区域嘛。噢~~似乎有点思路了哎。
平面被3条直线分成了7个区域,每个区域都将原来的一部分空间变成了两部分空间。也就是说,新增了7个空间。同上,如果我
们用b(3)来表示3个平面分了几个空间区域,那么b(4)就等于b(3)+a(3)。a(3)是什么?上面刚说的嘛,向上看,第一
个图的下面一段话。
看起来挺对的哎,就是还有点小犹豫。要不我们再看看5个平面的情况验证一下?
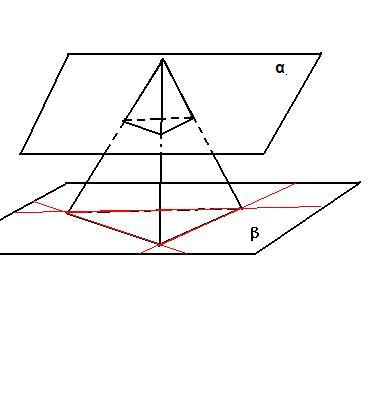
呃……好吧我画的真糟。:(
平面β和α是会相交的,而且如果要得到最多的空间区域,交线与其他平面和β的交线不平行。于是乎,问题又转换成了,4条
直线把平面分成了多少区域。所以呢,b(n)真的等于b(n-1)+a(n-1)。
好啦,我要得出结果啦。b(n) = n+1+(n+1)*n*(n-1)/6
别问我结果怎么推出来的,二阶等差嘛。。
呃……其实我数学超烂,1×2+2×3+3×4+……+(n-1)×n 等于多少不会算,还是请教了FancyMouse殿下,林杰杰,flyfox,
ailyanlu,tdzl众牛才会算:(好笨。原理是C(a,a)+C(a+1,a)+...+C(b,a)=C(b+1,a+1),把a换成2,b换成n可以直接得到。也或者1×2+2×3+3×4+……+(n-1)×n = (1^2+2^2+3^2+……+n^2)-(1+2+3+……+n) = n×(n+1)×(2n+1)/6-(n+1)×n/2。
囧ing