秦曾昌人工智能课程---4、梯度下降算法
一、总结
一句话总结:
找wi:注意,普通的梯度算法是找wi,而不是优化wi
1、比如我们现在求身高体重对性别的影响,那么输入数据中包含身高和体重,那么输入数据是 标量还是矢量?
矢量:明显有方向,因为身高体重不能混为一谈
2、机器学习实例:根据某城市房子的大小和房价做机器学习的时候,具体思考的步骤是什么?
1、假设为线性模型:h0(x)=θ0+θ1x
2、计算不同(θ0,θ1)模型:并且计算对应的损失函数
3、画出损失函数图:比如θ0=0时,横轴θ,纵轴损失函数的值
3、上标(x(i),y(i))表示什么?
表示第i份数据
4、线性模型:h0(x)=θ0+θ1x(y=ax+b)如何化为向量的模式?
变成向量相乘:h0(x)=θ0+θ1x=θ0*x0+θ1*x1,其中x0=1,假设X上标T=(x0,x1),θ上标T=(θ0,θ1),则h0(x)=θ上标T * X
5、为什么梯度下降算法是 w1=w1-η·∂L/∂w1 这个函数?
损失函数图(U型):型根据损失函数图来参照的,L是损失函数,图的纵轴是L,横轴是w1
照图理解:解释为什么∂L/∂w1>0左移,反之右移
tan角度:∂L/∂w1表示对应切线的tan角度,也就是斜率为正那么这个数就是正的
6、梯度下降算法 w1=w1-η·∂L/∂w1 是优化w1 还是找到最小的w1?
其实是找到最小的w1:损失函数图(U型),如果点偏右,就左移,同理左边。移到U的最低点。
7、梯度下降算法 w1=w1-η·∂L/∂w1 的实质是什么?
找w1最小值:注意是找w1的最小值,而不是优化w1
8、梯度下降算法 w1=w1-η·∂L/∂w1 的 算法实现是什么?
递归:因为是通过不断的迭代w1
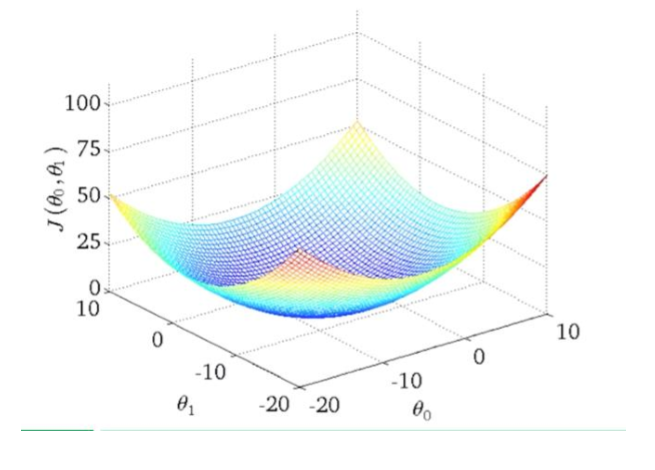
9、如果有两个参数θ0,θ1,那么损失函数的图长什么样?
网兜:相当于U函数的立体化,纵轴是L(θ0,θ1),横轴两个分别是θ0,θ1
等高线:如果投影到平面的话,那就是等高线
10、画图讲课做笔记软件(TOOLS)?
AI Class
11、梯度下降算法 w1=w1-η·∂L/∂w1 中的学习速率η一定要做成自适应么?
不是:损失函数是U型的,举例最低点远的时候∂L/∂w1斜率比较大,那么η·∂L/∂w1也比较大,距离近的时候已经自动跨小步了
12、求导函数df(g(x))/dx怎么求导?
外导*内导:df(g(x))/dx=f'(g(x))*g'(x)
13、梯度下降算法 w1=w1-η·∂L/∂w1 对 多维参数 的时候公式怎么写?
多乘[x上标i]:wi=wi-η·∂L/∂wi*[x上标i],当i=0时,[x上标i]=1,[x上标i]表示第i个数据
14、为什么多维的损失函数的截面会变成很多椭圆?
wi的大小不一样:wi=wi-η·∂L/∂wi*[x上标i]
将[x上标i]归一化:将椭圆化为圆的话可以优化查询
15、归一化两种方法?
正数0-1:xj=xj/(max(xj)-min(xj))
圆:xj=xj-x平均/(max(xj)-min(xj))
16、监督学习中的Regression(Predict)是什么?
预测问题:给输入,得到一个输出,而不是做拟合
17、最小二乘法是什么?
误差的平方和为最小:使得这些求得的数据与实际数据之间误差的平方和为最小
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
18、复杂函数f(x)如何求解?
随机取一个点,循环->【取斜率,取斜率与x轴交点,取这个交点】,图如[女]去掉横并且翻转成直角坐标系
19、如何解决梯度下降算法取到 局部最优解的情况?
优化损失函数:构造的损失函数尽量不要拐那么多弯
随机取多个点:随机在损失函数上取多个点
二、内容在总结中