纠删码(Erasure Code)中的数学知识
背景
在数据存储领域,Hadoop采用三副本策略有效的解决了存储的容错问题,但是三副本策略中磁盘的利用效率比较低,仅有33%,而且副本带来的成本压力实在太高,后来适时的出现了纠删码的概念。当冗余级别为n+m时,将这些数据块分别存放在n+m个硬盘上,这样就能容忍m个(假设初始数据有n个)硬盘发生故障。当不超过m个硬盘发生故障时,只需任意选取n个正常的数据块就能计算得到所有的原始数据。纠删码以更低的存储成本备受青睐,目前Microsoft、Google、Facebook、Amazon、淘宝(TFS)都已经在自己的产品中采用了Erasure Code.
在以上背景的基础上,本文在纠删码的编码、解码中采用的矩阵数学知识,以及矩阵分解中用到的LU分解等数学知识进行分析,并在文末给出相应的代码示例。
纠删码工作原理简介:
RS(Reed-Solomom)码是一种比较常见的纠删码,它的两个参数m和n分别代表校验块个数和原始数据块个数。
纠删码编码过程:
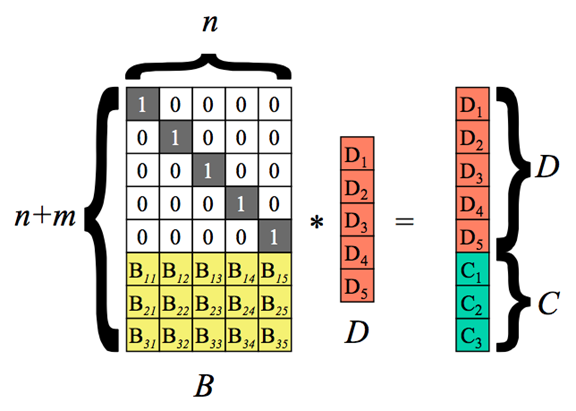
在图中的编码过程,C代表校验块,D代表原始的数据块。
当丢失了部分数据,如图
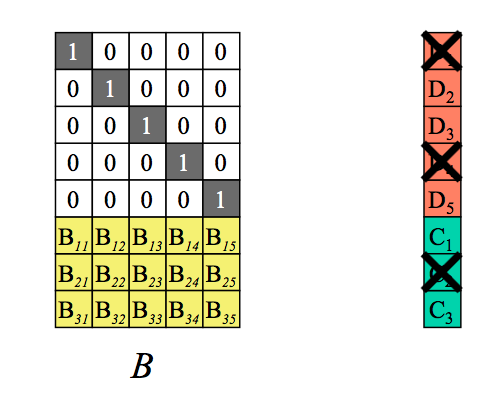
纠删码解码过程:
Step1:在编码矩阵中去掉丢失数据块以及该数据块对应的行。即B矩阵变为了n*n 维度的方阵,C与D组合的矩阵由(n+m)行变为n行,在上述假设过程中,我们得到新的矩阵以及对应的矩阵运算关系式,其中在丢失了部分数据块后,D所代表的原始数据块便成为了要求的目标。
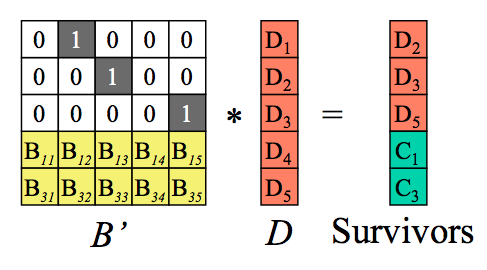
Step2:求B’的逆矩阵。
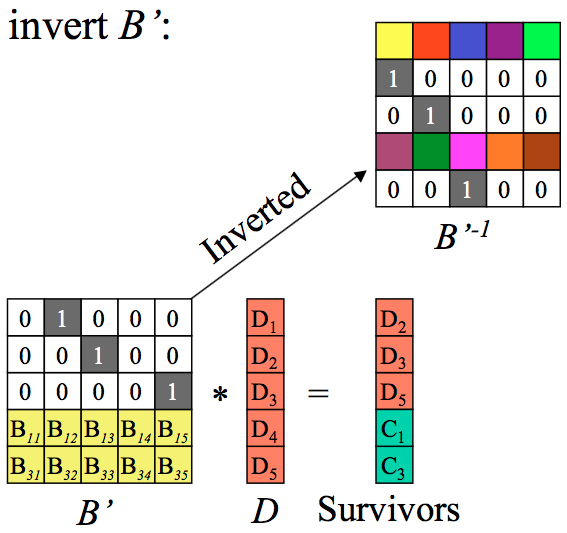
Step3:可以采用对等式两边同时乘上B’的逆矩阵,于是得到所求解。


为了保证B’逆矩阵是存在的,必须保证B’矩阵是可逆的,在通常的计算过程中,用于校检的黄色部分数据块采用范德蒙矩阵。
函数Inverse[B′]代表B'的逆矩阵,I代表单位矩阵:
Inverse[B′]∗B′∗D=Inverse[B′]∗S I∗D=Inverse[B′]∗S D=Inverse[B′]∗S
Python模拟纠删码数据恢复的流程
# Erasure Code
import numpy as np
# 备份数量
backup_up = 2
# 原始数据
data = np.array([1, 2, 3, 4, 5])
# 根据纠删码原理生成的数据
vander_data = np.concatenate((np.identity(len(data)), np.vander(data, 3).transpose()::-1]), axis=0)
storage_data = vander_data.dot(data)
print('生成数据',storage_data)
# 模拟数据丢失
loss_data = np.concatenate((storage_data[0:3], storage_data[5:7]), axis=0)print('丢失后数据', loss_data)
# 恢复数据
recover_data = np.linalg.inv(np.concatenate((vander_data[0:3], vander_data[5:7]), axis=0)).dot(loss_data)
print('恢复数据',recover_data)
# 输出结果
# 生成数据 [ 1. 2. 3. 4. 5. 15. 55. 225.]
# 丢失后数据 [ 1. 2. 3. 15. 55.]
# 恢复数据 [1. 2. 3. 4. 5.]
正交分解
矩阵的正交分解又称为QR分解,是将矩阵分解为一个正交矩阵Q和一个上三角矩阵的乘积的形式。任意实数方阵A,都能被分解为 。这里的Q为正交单位阵,即 R是一个上三角矩阵。这种分解被称为QR分解。 QR分解也有若干种算法,常见的包括Gram–Schmidt、Householder和Givens算法。 QR分解是将矩阵分解为一个正交矩阵与上三角矩阵的乘积。这里仅记录一下第一种分解的计算过程(Matlab代码以及例题计算过程)。
Schmidt正交化
定理1 设A是n阶实非奇异矩阵,则存在正交矩阵Q和实非奇异上三角矩阵R使A有QR分解;且除去相差一个对角元素的绝对值(模)全等于1的对角矩阵因子外,分解是唯一的.
定理2 设A是m×n实矩阵,且其n个列向量线性无关,则A有分解A=QR,其中Q是m×n实矩阵,且满足QHTQ=E,R是n阶实非奇异上三角矩阵该分解除去相差一个对角元素的绝对值(模)全等于1的对角矩阵因子外是唯一的.用Schmidt正交化分解方法对矩阵进行QR分解时,所论矩阵必须是列满秩矩阵。
算法步骤
- 写出矩阵的列向量;
- 列向量按照Schmidt正交化正交;
- 得出矩阵的Q′,R′;
- 对R′的列向量单位化得到Q,R′的每行乘R′每列的模
matlab代码
function[X,Q,R] = QRSchmidt(A,b)
%方阵的QR的Gram-Schmidt正交化分解法,并用于求解AX=b方程组[m,n]=size(A);
if m~=n
%如果不是方阵,则不满足QR分解要求
disp('不满足QR分解要求');
end
Q=zeros(m,n);
X=zeros(n,1);
R=zeros(n);
for k=1:nR(k,k)=norm(A(:,k));
if R(k,k)==0
break;
end
Q(:,k)=A(:,k)/R(k,k);
for j=k+1:n
R(k,j)=Q(:,k)'*A(:,j);
A(:,j)=A(:,j)-R(k,j)*Q(:,k);
end
if nargin==2
b=Q'* b;
X(n)=b(n)/R(n,n);
for i=n-1:-1:1
X(i)=(b(i)-sum(R(i,i+1:n).*X(i+1:n)'))/R(i,i);
end
else
X=[];
end
end
手撕计算过程

matlab自带方法
%产生一个3*3大小的魔方矩阵
A=magic(3)
[Q,R]=qr(A)