| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
|---|---|
| 这个作业的地址 | DS博客作业05--查找 |
| 这个作业的目标 | 学习图结构设计及相关算法 |
| 姓名 | 杨振鹏 |
0.PTA得分截图

1.本周学习总结
1.1 查找的性能指标
ASL(Average Search Length)
ASL,是查找算法的查找成功时的平均查找长度的缩写,是为确定记录在查找表中的位置,需和给定值进行比较的关键字个数的期望值。
ASL:关键字的平均比较次数,也叫做平均搜索长度。
公式:ASL=∑(i=1->n)p(i)*c(i);其实就是ASL=n个关键字找到时的比较次数之和/n
1.2 静态查找
- 顺序查找
定义:按照序列原有顺序对数组进行遍历比较查询的基本查找算法
类似与数组查找,一个一个按顺序的找
int SeqSearch(Seqlist R,int n,KeyType k)
{
int i=0;
while(i<n&&R[i].key!=k)i++;//从表头开始找
if(i>=n)return 0;//没找到返回0
else return i+1;//找到返回序号i+1
}

- 二分查找
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列.
int binarySearch(SeqList R,int n,KeyType k){
int low = 0, high = n-1, mid;
while(low <= high){
mid = (low + high) / 2;
if(R[mid.key] == k)return mid;//找到就返回下标
else if(R[mid].key > k)high = mid - 1;
elss low = mid + 1;
}
return 0;//找不到返回0
}
//递归法
int BinarySearch(SeqList R,int low,int hight,KeyType k)
{
int mid;
if(low<=high){//查找的区间存在一个以上的元素
mid=(low+high)/2;//找中间位置
if(R[mid].key==k)return mid+1;//查找成功,返回序号mid+1
if(R[mid].key>k)BinarySearch(R,low,miid-1,k);//在[low…mid-1]区间递归寻找
else BinarySearch(R,mid+1,high,k); //在[mid+1…high]区间递归寻找
}
else return 0;
}
ASL成功=每一层节点数层次数的总和/总结点数
ASL不成功=其他不存在于树中的每一层节点数(层次数-1)/总结点数
1.3 二叉搜索树
1.3.1 如何构建二叉搜索树(操作)
eg.12 7 17 11 16 2 13 9 21 4

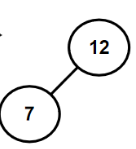

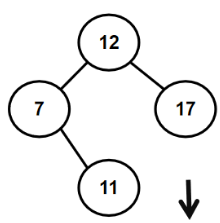

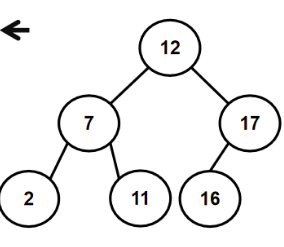

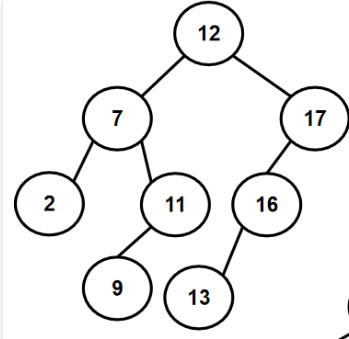
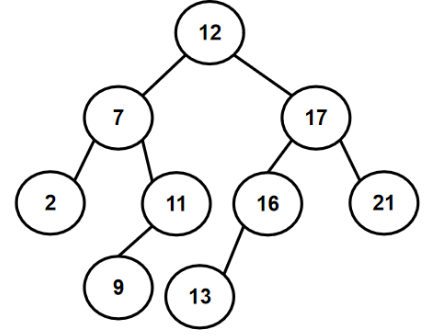
1.3.2 如何构建二叉搜索树(代码)
- 二叉树搜索树结构体定义
typedef char* InfoType; //其他数据类型
typedef struct node
{
KeyType key; //关键字域
InfoType data; //其他数据域
struct node *lchild, *rchild;/*左右孩子*/
}BSTNode, * BSTree;
- 二叉搜索树的构建
void CreateBST(BinTree& BST, int n)/*建树函数*/
{
int x;
BST = NULL;//树初始化为空
for (int i = 0; i < n; i++)
{
cin >> x;
Insert(BST, x);
}
}
- 二叉搜索树的插入
void Insert(BinTree& BST, int X)
{
if (BST == NULL)/*树空*/
{
BST = new TNode;/*申请*/
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
}
else if (X > BST->Data)/*大于插左边*/
{
Insert(BST->Left, X);
}
else if (X < BST->Data)/*小于插右边*/
{
Insert(BST->Right, X);
}
}
- 二叉搜索树的查找
BinTree Find(BinTree BST, ElementType X)
{
if (BST == NULL)
{
return NULL;/*为空返回空*/
}
if (X > BST->Data)
{
Find(BST->Right, X);/*大于在右*/
}
else if (X < BST->Data)
{
Find(BST->Left, X);/*小于在左*/
}
else
{
return BST;/*找到则返回*/
}
}
- 二叉搜索树的删除
BinTree Delete(BinTree BST, ElementType X)
{
BinTree storage;
if (BST == NULL)/*为空*/
{
printf( "Not Found
");
return BST;/*输出并返回根节点*/
}
if (X > BST->Data)
{
BST->Right = Delete(BST->Right, X);
}
else if (X < BST->Data)
{
BST->Left = Delete(BST->Left, X);
}
else
{
if (BST->Left && BST->Right)/*左右子树都存在*/
{
storage = FindMin(BST->Right);/*找右子树的最小点*/
BST->Data = storage->Data;
BST->Right = Delete(BST->Right, BST->Data);
}
else
{
storage = BST;
if(BST->Left==NULL)/*左为空*/
{
BST = BST->Right;
}
else/*右为空*/
{
BST = BST->Left;
}
free(storage);/*删除*/
}
}
return BST;
}
时间复杂度:最好:O(logn),最差:O(n)
用递归实现插入、删除的优势
保留父子关系,便于删除和插入顺利找到父亲和孩子
代码简短,便于书写,树的递归更能掌握
1.4 AVL树
由于二叉搜索树存在数据分配不平衡的现象,会导致查找时的时间复杂度提高,所以诞生了AVL解决此类问题。
AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树
- 结构体定义
typedef struct node
{
KeyType key; //关键字域
int bf; //平衡因子
InfoType data; //其他数据域
struct node *lchild, *rchild;/*左右孩子*/
}BSTNode, * BSTree;
- 4种调整
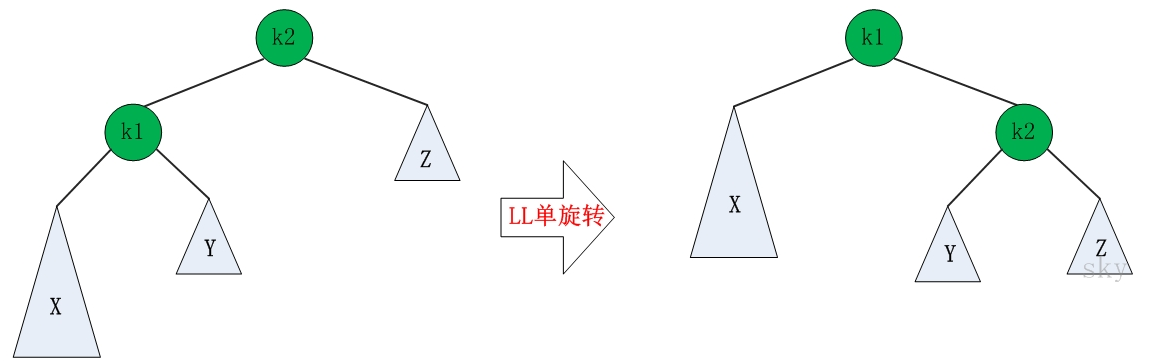
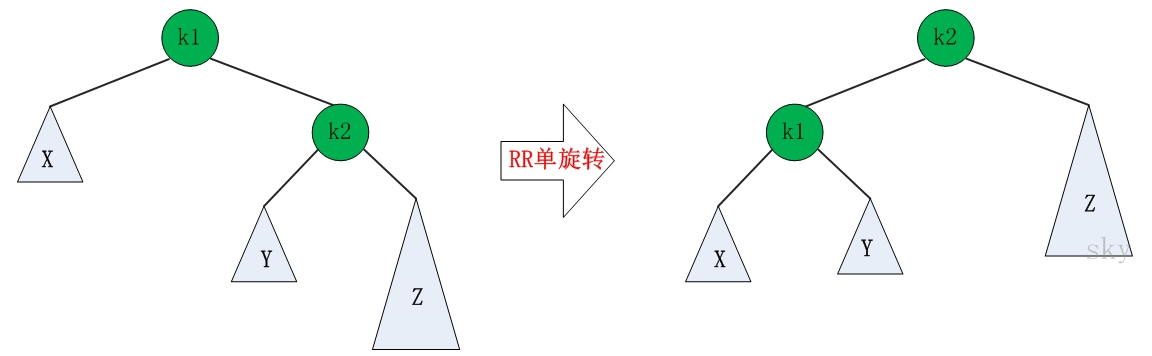


AVL树的高度和树的总节点数n的关系:h≈log2N(h)+1
map--STL
基本概念
map是STL中非常有用的一个容器
和函数类似,map是通过键值key查询对应value
对于数组而言,其下标必须非负整数的数值,且数值不能过大,而map就不同了,map的键值可以是任意类型,包括最常用的string类型,map的value也同样可以为任意类型
用途
map的内部是红黑树实现,其具有自动排序的功能
通过键值排序,以递增的方式排序
若键值为整形,以数值递增排序
若键值为string,以字符串升序排序
- 用法
begin() 返回指向 map 头部的迭代器
clear() 删除所有元素
count() 返回指定元素出现的次数
empty() 如果 map 为空则返回 true
end() 返回指向 map 末尾的迭代器
erase() 删除一个元素
find() 查找一个元素
insert() 插入元素
key_comp() 返回比较元素 key 的函数
lower_bound() 返回键值>=给定元素的第一个位置
max_size() 返回可以容纳的最大元素个数
rbegin() 返回一个指向 map 尾部的逆向迭代器
rend() 返回一个指向 map 头部的逆向迭代器
size() 返回 map 中元素的个数
swap() 交换两个 map
upper_bound() 返回键值>给定元素的第一个位置
value_comp() 返回比较元素 value 的函数
1.5 B-树和B+树
B-树和AVL树区别
AVL树结点仅能存放一个关键字,树的敢赌较高,而B-树的一个结点可以存放多个关键字,降低了树的高度,可以解决大数据下的查找
B-树定义:一棵m阶B-树或者是一棵空树,或者满足一下要求的树就是B-树
每个结点之多m个孩子节点(至多有m-1个关键字);
除根节点外,其他结点至少有⌈m/2⌉个孩子节点(至少有⌈m/2⌉-1个关键字);
若根节点不是叶子结点,根节点至少两个孩子
- 结构体定义
typedef int KeyType; //关键字类型
typedef struct node
{
int keynum;/*节点当前存储的关键字个数*/
KeyType key[MAX]; //关键字域
struct node* parent;/*双亲节点指针*/
struct node* ptr[MAX];/*孩子节点指针数组*/
}BTNode;
-
插入


-
删除
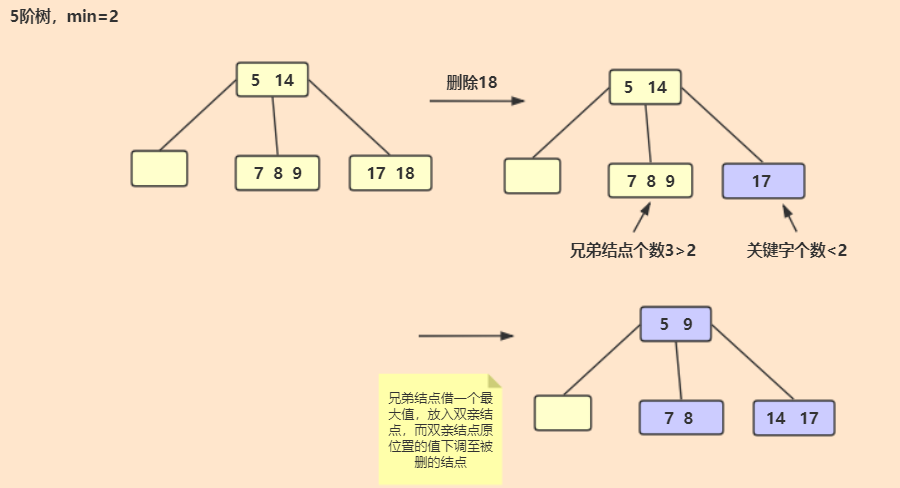

1.6 散列查找
哈希表(又称散列表),是一种存储结构,适用于记录的关键字与存储的地址存在某种关系的数据。
基本思路是,设要存储的元素个数为n,设置一个长度为m的连续内存单元,以每个元素的关键字ki(i取值为0~n-1)为自变量,通过一个称为哈希函数的函数h(ki),把ki映射为内存单元的地址(或下标),并把该元素存储在这个内存单元中,这个地址也称为哈希地址。这样构造的线性存储结构就是哈希表。
- 直接取地址法
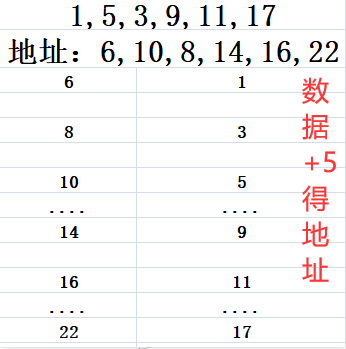
- 除留余数法

- 数字分析法

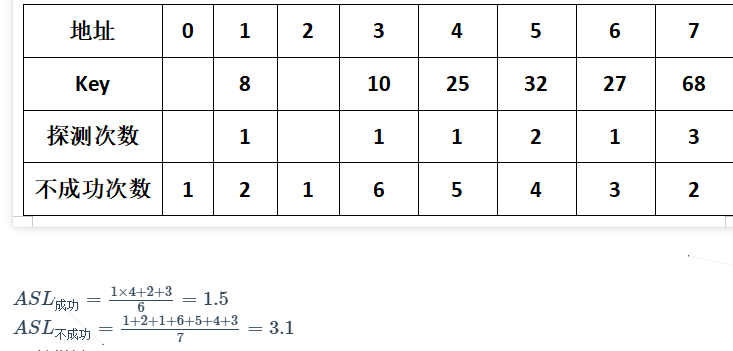
- 开放地址法
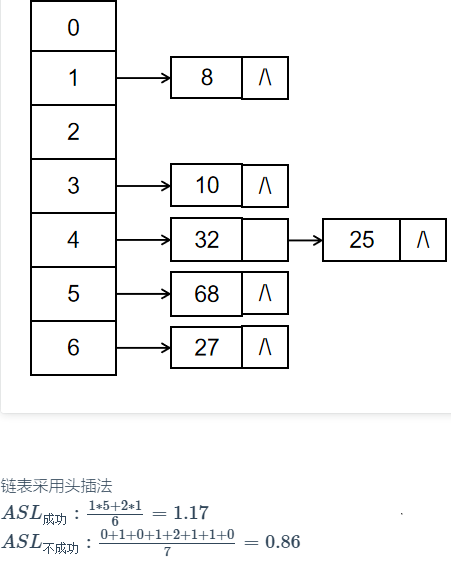
- 拉链法
2.PTA题目介绍
2.1 是否完全二叉搜索树
- 思路
构造二叉搜索树
根据二叉搜索树的定义,若左子树不空,左子树的所有结点的值都要比根节点小;若右子树不空,右子树所有节点的值都比根节点大,且左右子树也都是二叉排序树。同时,中序遍历的二叉搜索树可以得到一个递增的序列。
根据题意,该题定义的二叉搜索树是初始为空的且左子树键值大,右子树键值小。所以,该中序遍历后是一个递减的序列,在构造的时候需要让待插入比当前结点小的结点作为右子树,比当前结点大的作为左子树。
判断是否为完全二叉搜索树
根据完全二叉搜索树的定义,若设二叉树的高度为h,除最后一层外,其它各层 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。且层次遍历时遇到第一个空结点层次遍历恰好结束,如果遍历到一个结点只有左孩子,或者左右孩子均为空时,那么剩余未遍历的结点,全都是叶子结点。
- 伪代码
函数:
void Insert(BinTree*& BST, int k);//把结点k插入二叉排列树中
bool IsCompleteBinaryTree(BinTree*& BST, int n);//判断是否为完全二叉树
void LevelOutput(BinTree *BST);//层次遍历输出
构造二叉搜索树://注意:题目要求左子树键值大,右子树键值小
如果BST为空
建立新结点
如果结点k<BST->key
递归进入右子树
如果结点k>BST->key
递归进入左子树
判断是否为完全二叉树://即判断是否所有结点都已经遍历
queue存储树结点的队列
定义变量num来判断是否所有结点都已经遍历
if 树空
也算作是完全二叉树,返回true
end if
先把树的根节点放入队列
while 1
取队首node
如果为空则跳出循环
不为空则让左右子树进栈,先左后右
出栈队首并使得输出个数num增1
end while
判断num的值,等于节点个数n则说明在遇到空节点前树节点遍历完成,返回true,反之,则返回false
层次遍历输出类似于判断是否为完全二叉树的函数,其实两个函数可以结合
- 代码
#include<stdio.h>
#include<stdlib.h>
struct TNode {
int Data;
struct TNode *Left, *Right;
};
struct TNode *Insert(struct TNode *BST, int X) //搜索二叉树的插入
{
if(!BST) {
BST = (struct TNode *)malloc(sizeof(struct TNode));
BST->Data = X;
BST->Left = BST->Right = NULL;
}
else {
if(X > BST->Data) {
BST->Left = Insert(BST->Left, X);
}
else if(X < BST->Data) {
BST->Right = Insert(BST->Right, X);
}
}
return BST;
}
int LevelorderTraversal(struct TNode *BT) //层序遍历
{
int t = 0, k = 1, flag = 1;
/*t是队头指针,k为队尾指针,flag用于标记是否为完全二叉树,非0即真
*flag == 2为标记,如果flag==2之后的所有结点不全为叶子节点,为否*/
struct TNode *s[21]; //队列大小
s[t] = BT; //第一个二叉树根结点入队列
while(t != k) { //t于k相等说明,队列为空(此非循环队列)。
if(!t) {
printf("%d", s[t]->Data); //第一个打印不用空格
}
else {
printf(" %d", s[t]->Data); //除第一个以外,其他前面加空格,这样保证了结尾不会有空格
}
if(s[t]->Left && s[t]->Right) { //若左右结点都不为空
if(flag == 2) { // 如果此结点已被标记,而此节点不为叶子,则不为完全二叉树
flag = 0; //标记为否
}
//遍历继续
s[k++] = s[t]->Left; //左子树入队
if(t == k) {
break;
}
s[k++] = s[t]->Right; //右子树入队
if(t == k) {
break;
}
}
else if(s[t]->Left && (!s[t]->Right)){ //如果左子树不为空,右子树为空
if(flag == 2) { // 如果此结点已被标记,而此节点不为叶子,则不为完全二叉树
flag = 0; //标记为否
}
//遍历继续
s[k++] = s[t]->Left;//左子树入队
if(flag != 0) { //如果此树已经确定不为完全二叉树,则不必标记
flag = 2; //若此树未被标记,则在此处标记,后面的节点需都为叶子才是完全二叉树,否则不是
}
if(t == k) {
break;
}
}
else if(!s[t]->Left && s[t]->Right){ //左子树为空,而右子树不为空,则此树一定是非完全二叉树
flag = 0; //标记为否
s[k++] = s[t]->Right; //右子树入队
if(t == k) {
break;
}
}
else { //如果左右子树都为空
if(flag == 1) { //并且此树还认为正确的
flag = 2; //标记为不一定正确
}
}
t ++; //队头指针右移,用于出队
}
return flag; //返回flag的值
}
int main()
{
int i, n, X, H;
struct TNode *BST = NULL;
scanf("%d", &n);
for(i = 0; i < n; i ++) {
scanf("%d", &X);
BST = Insert(BST, X);
}
if(LevelorderTraversal(BST) != 0) { //flag的值非0即真
printf("
YES
");
}
else {
printf("
NO
");
}
return 0;
}
- 提交列表

- 知识点
完全二叉树
完全二叉树是特殊形态的满二叉树,在满二叉树的基础上,它的叶子结点可以不全满,且叶子结点整体偏左。
层次遍历
借助队列来储存二叉树每一层的元素并依次输出。
二叉搜索树的插入操作
边查找边插入,算法中的根节点指针要用引用类型,这样才能将改变后的值传回给实参
2.2 航空公司VIP客户查询
- 思路
建立哈希链,取乘客的身份证号后5位作为哈希地址进行存储,如果不是会员则添加,是会员就看里程数
但这题借用map容器更加方便,但因为身份证最后一位校验码有x,则需要将x转化为数字
时间复杂度:O(n²)
- 伪代码
获得哈希表地址:
for i = 12 to i = 16
取后五位数字作为哈希地址
if 最后以为为x
temp乘10再累加
else
直接转换为五位数;
return temp;
在哈希链中寻找用户信息:
node = h[temp]->next;
while 当前用户有信息存储
if 用户信息与存档相匹配
return node;
else 用户信息与存档不相匹配
读取下一个信息;
end while
向哈希链中插入数据:
temp = GetID(ID);//获得信息·
p = Find(h, ID, temp);//核对信息
if 乘客是会员
if 要走的距离小于最小里程数
在本来的里程数上加上k算作最大里程
else
直接在原里程数上增加
end if
end if
else 乘客不是会员
新录入ta的信息成为会员
根据里程大小计算总里程
将新用户信息插入node中
end else
创建哈希链:
for i = 0 to i = n-1
输入ID以及航程dist
Insert(h, ID, dist, k);
end for
- 代码
#include <stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct node *Node;
struct node {
char*IDnumber;
int mileages;
Node Left,Right;
};
Node Tree[11]= {0};
Node Insert(Node,char*,int);
void query(Node,char*);
int main() {
int n,standard;
scanf("%d%d",&n,&standard);
char ID[19];
int mileage;
while(n--) {
scanf("%s %d",ID,&mileage);
if(mileage<standard)mileage=standard;
int Index=ID[17]-'0';
if(Index>9)Index=10;
Tree[Index]=Insert(Tree[Index],ID,mileage);
}
scanf("%d",&n);
while(n--) {
scanf("%s",ID);
int Index=ID[17]-'0';
if(Index>9)Index=10;
query(Tree[Index],ID);
}
return 0;
}
void query(Node T,char*ID) {
if(!T) {
printf("No Info
");
return;
}
int flag=strcmp(T->IDnumber,ID);
if(flag==0) {
printf("%d
",T->mileages);
} else if(flag>0)query(T->Left,ID);
else query(T->Right,ID);
}
Node Insert(Node h,char*a,int K) {
if(!h) {
Node temp=(Node)malloc(sizeof(struct node));
temp->IDnumber=(char*)malloc(sizeof(char)*19);
strcpy(temp->IDnumber,a);
temp->mileages=K;
temp->Left=NULL;
temp->Right=NULL;
return temp;
} else {
int flag=strcmp(h->IDnumber,a);
if(!flag)h->mileages+=K;
else if(flag>0)h->Left=Insert(h->Left,a,K);
else h->Right=Insert(h->Right,a,K);
return h;
}
}
- 提交列表

- 知识点
哈希链的构造创建和寻找,建链前需要对哈希链进行初始化和申请空间。
哈希链拉链法的使用
2.3 基于词频的文件相似度
- 思路
本题设计一个倒排索引表结构实现,单词作为关键字。我使用的方法,即将文件按照单词的分类,存储到每个单词的结构中,最后一个结构中保存了该单词所含有的文件。对于每个单词而言,可以使用哈希链来做,不过这里可以用 STL 库的 map 容器来存放。 - 伪代码
定义int类型变量的两个文件内编号 file_a,file_b作为待查找的文件编号
定义变量类型为<string,int[]>的map容器构建单词索引表
根据单词在单词索引表中构建映射
for i=0 to 文件组数
输入文件编号
for iterator=map.begin() to !map.end()遍历单词
if 单词在两个文件都出现过
修正重复单词数,合计单词数
else if 单词在其中一个文件中出现过
修正合计单词数
end if
end for
end for
计算输出文件相似度
- 代码
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<string>
#include<map>
#include<stack>
#include<vector>
#include<algorithm>
#include<sstream>
#include<set>
#include<iostream>
using namespace std;
#define inf 0x3f3f3f
int main()
{
int n,m,x,y,i,j,l;
cin>>n;cin.get();
map<string,int> a[105];
string s;
for(j=1;j<=n;j++)
{
while(getline(cin,s))
{
if(s=="#")break;
stringstream ss(s);
while(ss>>s)
{
string op="";
i=0;
while(i<s.size())
{
if(s[i]>='A'&&s[i]<='Z')
op+=s[i]+32;
else if(s[i]>='a'&&s[i]<='z')
op+=s[i];
else
{
if(op.size()<3);
else if(op.size()>10)
{
op=op.substr(0,10);
a[j][op]++;
}
else a[j][op]++;
op.clear();
}
i++;
}
if(op.size()<3)continue;
else if(op.size()>10)
{
op=op.substr(0,10);
a[j][op]++;
}
else a[j][op]++;
}
}
}
scanf("%d",&m);
while(m--)
{
scanf("%d%d",&x,&y);
int sum=0;
for(map<string,int>::iterator it=a[x].begin();it!=a[x].end();it++)
{
if(a[y].count(it->first))sum++;
}
if((int)a[x].size()+(int)a[y].size()-sum==0)printf("0.0%%
");
else printf("%.1f%%
",100.*sum/((int)a[x].size()+(int)a[y].size()-sum));
}
}
- 提交列表
