D. Black Hills golden jewels
In Rapid City are located the main producers of the Black Hills gold jewelry, a very popular product among tourists. The main characteristics of these jewels are the designs of leaves and grape clusters that are made with gold alloys in yellow, green and pink tones.
Planning a trip to Rapid City in 2017, Nay Suames decides that he wants to buy these famous jewels, but he doesn't have much money to spend. Searching for the lowest prices, he found a jewelry store that will have a sale in May, the same month he will travel to that city. Lucky guy!
The jewelry store intends to sell the jewels that were produced with small defects, in general, only perceivable by experts. The jewels are separated in N categories of defects. Even if the defect is imperceptible, the jewelry store can't sell the jewel at full price, so it gives a discount proportional to the defect.
Knowing the high demand for these jewels, the jewelry store created a system aiming to be fair and, at the same time, to prevent everybody from buying only the cheapest jewels. The clients have to make a queue and will be served one at a time. When their time comes, the client must choose two jewels from different categories. Furthermore, they can't choose the same combination of categories that was previously chosen by another client.
Nay asks for your help to find the minimum amount of money he needs, being the K-th client in the queue, so that it is guaranteed that he can buy two different jewels.
The first line contains two integers, N and K, 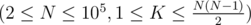 , representing the number of categories and the position of Nay in the queue, respectively. The next line contains N integers a1, a2, ..., aN (0 ≤ ai ≤ 109), corresponding to the prices of each category.
, representing the number of categories and the position of Nay in the queue, respectively. The next line contains N integers a1, a2, ..., aN (0 ≤ ai ≤ 109), corresponding to the prices of each category.
Print a single integer, the minimum amount of money to guarantee that Nay can buy the jewels.
4 3 2 4 5 2
6
6 9 1 2 3 4 5 6
7
【题意】:内容介绍了很多,其实跟题意没什么关系。关键的题意可以浓缩成,给定一个序列,从序列中任意取两个数形成一个和,两个数不可相同,要求求出第k小的组合。
【分析】:数据量是10的五次方,任取两个记录下来的话是10的10次方级的,再拍个序的话,肯定既超控件又超时间。但10的五次方级别的是可以拍个序的,排完序后就可以确定拿取组合的上限即最大和次大元素的组合,最小组合即最小和次小元素的组合。确定了上限和下限,又因为所求的值是有单调性的,所以考虑用二分。
在确定使用二分之后,此时需要验证一个值是否满足条件。即任意组合中不大于该组合的组合数是否不小于k。若不小于k的话,则不断向左侧区间逼近,求出最小的符合的值。在求取组合数目时,如果使用普通的二重循环的话,肯定又超时。此时从最小的元素开始,设x为验证元素,使用upper_bound函数求出第一个大于x-a[i]的元素的位置,其函数返回的值即是和该元素相加不大于x的个数,即是组合数。upper_bound函数本质上也是一个二分。在此基础上可以进行一定的优化,在循环过程中只要所记数值大于等于k就可结束循环。知道大于x的a[i]标记,缩小循环范围也可优化。
【代码】:

#include <bits/stdc++.h> using namespace std; //#pragma comment(linker, "/STACK:1024000000,1024000000") #define FIN freopen("input.txt","r",stdin) #define FOUT freopen("output.txt","w",stdout) typedef __int64 LL; const int MAXN = 1e5 + 5; const LL INF = 0x3f3f3f3f3f3f3f3f; LL A[MAXN]; LL N, K; bool check (LL m) { LL ks = 0; for (int i = N - 1; i >= 1; i --) { ks += lower_bound (A, A + i, m - A[i]) - A; } if (ks >= K) return true; return false; } int main() { #ifndef ONLINE_JUDGE FIN; //FOUT; #endif while (~scanf ("%I64d %I64d", &N, &K) ) { for (int i = 0; i < N; i ++) { scanf ("%I64d", &A[i]); } sort (A, A + N); LL lb = -1, ub = INF, mid; while (lb <= ub) { mid = (ub + lb) >> 1; if (check (mid) ) { ub = mid - 1; } else { lb = mid + 1; } } printf ("%I64d ", ub); } return 0; }
