求给出第 K (0 < K < 109) 个 N (0 < N < 44) 位二进制数,该二进制数不得有相邻的“1”。
这道题要求给出第 K (0 < K < 109) 个 N (0 < N < 44) 位二进制数,该二进制数不得有相邻的“1”。由于时间限制是 0.5 秒,肯定不能使用蛮力搜索从 1 列举到 K。
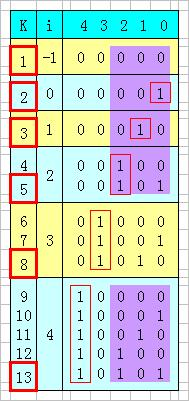
我们以 N = 5 来分析看看有没有什么规律。如左图所示,我们发现该二进制数最左边的“1”开始在第几个数之后出现是很规律的,如下所示(左图中红色粗框中的数):
1, 2, 3, 5, 8, 13, ...
也就是说,后项等于前二项之和。这不正是扔掉第一项后的斐波那契 ( Fibonacci ) 数列吗?
于是,程序在第 35 到 42 行的 GetFibonacci() 方法中计算出该数列。然后在第 22 到 33 的 GetBinarys() 方法中计算出第 K 个满足条件的二进制数。该方法在第 26 到 31 行的循环中从高位到低位设定“1”(如左图中红色细框所示)。
请注意,左图中两块阴影部分的内容是相同的,都代表了 N = 3 的情况。也就是说,N = 5 的最低三位是在重复 N = 3 的情况。并且由于该二进制数不得有相邻的“1”,所以在程序第 28 行使用 i - 2 而不是 i - 1 作为第 2 个参数调用 Seek() 方法,然后在第 30 行将该二进制数的第 i 位设为“1”。最后在第 26 行 k -= fib[i],以进入下一轮循环,直到 k 降低到 1 而结束循环。
本程序的算法应该是最优的,其时间复杂度为 O(N)。本程序的运行时间是 0.078 秒,其 C++ 版本程序的运行时间是 0.001 秒。
我们知道,斐波那契 ( Fibonacci ) 数列定义如下:
F1 = 1, F2 = 1, Fn = Fn-1 + Fn-2 (n > 2)
她的前几项如下:
DP关键在于找到状态转移方程,而找方程关键在于找状态。我们从限制条件开始构造状态。以位数N和K构造是不现实的,数据量太多,我们可以位数为N的二进制数的个数作为状态,这样如果第i位填0则f[i] = f[i-1] 如果第i位填1则第i-1位只能填0,此时f[i] = f[i-2]总之,f[i] = f[i-1] + f[i-2];这个就是传说中的转移方程。
然后考虑第K个的问题,因为开头为0的数必然排在开头为1的数的前面。也就是位数为N的数共有f[i]个,其中前面的是以0开头的f[i-1]个,后面是以1开头的f[i-2]个,所以如果K小于等于f[i-1]则其第i位必然为0,然后去考虑第i-1位,此时K不变;否则其第i位必然为1第i-1位必然为0,然后去考虑第i-2位,此时K= K-f[i-1]。
K= K-f[i-1]?
一个串,把右端的叫低位,叫第1位,左端的叫高位,叫第43位,(最多这么多位)
dp[n][0],表示第n位放0,到第1位,一共能产生多少个串
dp[n][1],表示第n位放1,到第1位,一共能产生多少个串
如果按照字典序来排,肯定第n位放0的话,字典序比放1的要小(无需考虑后面的)
现在要找第m个排序,看看第n位放0的话,能产生多少个排列,如果放0,产生的排序数都不够m大,那么这一位肯定是放1的,放了1,就应该从m-dp[n][0]重新考虑了,因为相当于你排除了放0的所有情况
求dp数组是一个从低位向高位编码的过程
求第m个排列,是一个从高位向低位解码的过程,解码就是从高位到低位,一位一位地确定到底是放1还是放0