前言
其实就是预处理+线段树。
目的:把树拆成链再用线段树处理(其实还是一种暴力,只是有点优化)。
为什么不直接拆成从根节点到每一个叶子结点的链?
假如更改一个节点(有多个子节点),那么就要修改几个线段树中的值了,会影响效率。
所以在这些链中不能有重叠部分。
为了提高线段树的效率,我们要尽量把一条链搞长一点,而不是更多的链。
所以我们就想到了下方预处理的办法。
先来回顾几个问题:
-
将树从(x)到(y)结点最短路径上所有节点的值都加上(z)(树上差分即可);
-
求树从(x)到(y)结点最短路径上所有节点的值之和(LCA即可);
-
将以(x)为根节点的子树内所有节点值都加上z(dfs序+差分即可);
-
求以(x)为根节点的子树内所有节点值之和(同3)。
但是:假如把几个问题放在一起咋做?
于是树链剖分闪亮登场!
准备
先说些概念:
-
重儿子:父亲节点的所有儿子中子树结点数目最多((sz)最大)的结点;
-
轻儿子:父亲节点中除了重儿子以外的儿子;
-
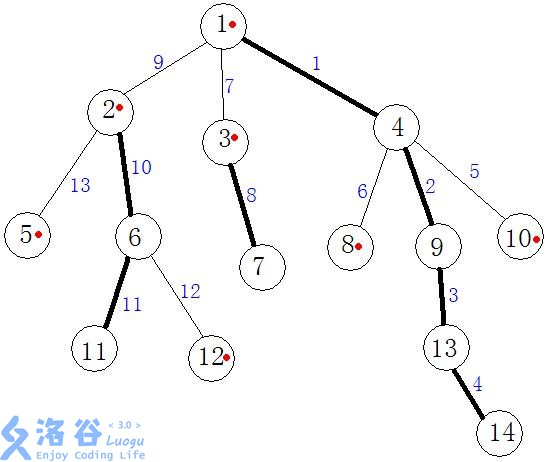
重边:父亲结点和重儿子连成的边(下图加粗);
-
轻边:父亲节点和轻儿子连成的边;
-
重链:由多条重边连接而成的路径;
-
轻链:由多条轻边连接而成的路径。
对数组的一些解释:
| 名称 | 解释 |
|---|---|
| (f[u]) | 保存结点(u)的父亲节点 |
| (dep[u]) | 保存结点(u)的深度值 |
| (sz[u]) | 保存以(u)为根的子树节点个数 |
| (son[u]) | 保存重儿子 |
| (top[u]) | 保存当前节点所在链的顶端节点(上图红点) |
| (id[u]) | 保存树中每个节点剖分以后的新编号(DFS的执行顺序) |
我们的目标就是把上图拆成一下几条链:
(1 ightarrow4 ightarrow9 ightarrow13 ightarrow14)
(2−>6−>11)
(3−>7)
(5)
(8)
(10)
(12)
处理
预处理:求f、d、sz、son、dep数组
void dfs1(int u,int fa){
f[u]=fa;
dep[u]=dep[fa]+1;
sz[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa)continue;
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>sz[son[u]])son[u]=v;
}
}
结果:

预处理:求出top、rk、id数组(dfs序)
void dfs2(int u,int t){
top[u]=t;
id[u]=++cnt;
a[cnt]=w[u];
if(!son[u])return;
dfs2(son[u],t);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=son[u]&&v!=f[u])dfs2(v,v);
}
}
结果:
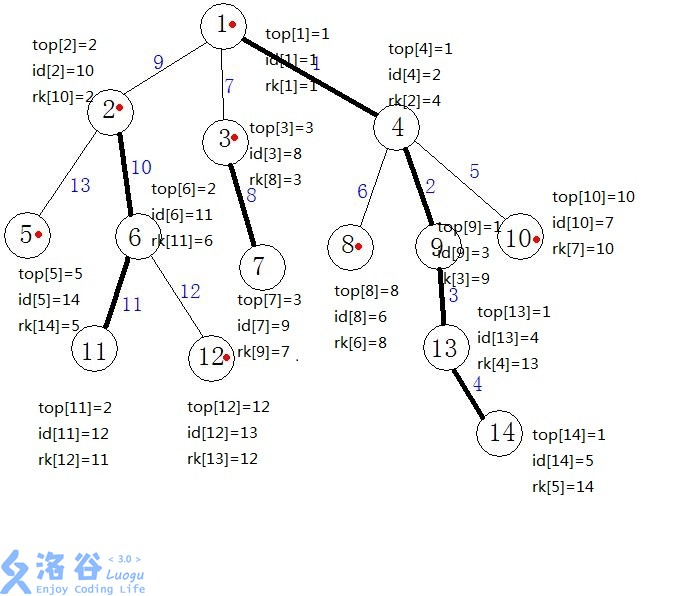
LCA操作咋办?有没有注意到top数组?它就是LCA中的"跳"的变形。
LCA
其实也可以不写。
妈妈再也不用担心我不会倍增啦!
这里使用了(top)来进行加速,因为(top)可以直接跳转到该重链的起始结点,轻链没有起始结点之说,他们的(top)就是自己。需要注意的是,每次循环只能跳一次,并且让结点深的那个来跳到(top)的位置,避免两个一起跳从而擦肩而过。
int lca(int x,int y){
int fx=top[x],fy=top[y];
while(fx!=fy){
if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
x=f[fx],fx=top[x];
}
return dep[x]<dep[y]?x:y;
}
修改链
在LCA的基础上也可以这么写:
void updata_lian(int x,int y,int z){
int fx=top[x],fy=top[y];
while(fx!=fy){
if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
updata(id[fx],id[x],z,1,cnt,1);
x=f[fx],fx=top[x];
}
if(id[x]>id[y])swap(x,y);
updata(id[x],id[y],z,1,cnt,1);
}
计贡献
在LCA的基础上也可以这么写:
int query_lian(int x,int y){
int fx=top[x],fy=top[y],sum=0;
while(fx!=fy){
if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
inc(sum,query(id[fx],id[x],1,cnt,1));
x=f[fx],fx=top[x];
}
if(id[x]>id[y])swap(x,y);
inc(sum,query(id[x],id[y],1,cnt,1));
return sum;
}
这样就差不多了。
上题:
没什么好说的。
注意一个点:(mod)不是题目固定的,也就是说:(a[i])可能大于(mod),甚至是几倍。
最好双重保险,函数返回前加一个取模。
出题人不要脸。
#include<bits/stdc++.h>
#define LL long long
using namespace std;
const LL N=1e5+10;
struct edge {
LL next,to;
} e[N*2];
struct node {
LL l,r,ls,rs,sum,lazy;
} a[N*2];
LL n,m,r,rt,mod,v[N],head[N],cnt,f[N];
LL son[N],d[N],size[N],top[N],id[N],rk[N];
void add(LL x,LL y) {
e[++cnt].next=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void dfs1(LL x) {
size[x]=1,d[x]=d[f[x]]+1;
for(LL v,i=head[x]; i; i=e[i].next) {
if((v=e[i].to)!=f[x])
{
f[v]=x,dfs1(v),size[x]+=size[v];
if(size[son[x]]<size[v])
son[x]=v;
}
}
}
void dfs2(LL x,LL tp) {
top[x]=tp,id[x]=++cnt,rk[cnt]=x;
if(son[x]) {
dfs2(son[x],tp);
}
for(LL v,i=head[x]; i; i=e[i].next) {
if((v=e[i].to)!=f[x]&&v!=son[x]) {
dfs2(v,v);
}
}
}
inline void up(LL x) {
a[x].sum=(a[a[x].ls].sum+a[a[x].rs].sum)%mod;
}
void build(LL l,LL r,LL x) {
if(l==r) {
a[x].sum=v[rk[l]],a[x].l=a[x].r=l;
return;
}
LL mid=l+r>>1;
a[x].ls=cnt++,a[x].rs=cnt++;
build(l,mid,a[x].ls),build(mid+1,r,a[x].rs);
a[x].l=a[a[x].ls].l,a[x].r=a[a[x].rs].r;
up(x);
}
inline LL len(LL x) {
return a[x].r-a[x].l+1;
}
inline void down(LL x) {
if(a[x].lazy) {
LL ls=a[x].ls,rs=a[x].rs,lz=a[x].lazy;
(a[ls].lazy+=lz)%=mod,(a[rs].lazy+=lz)%=mod;
(a[ls].sum+=lz*len(ls))%=mod,(a[rs].sum+=lz*len(rs))%=mod;
a[x].lazy=0;
}
}
void update(LL l,LL r,LL c,LL x) {
if(a[x].l>=l&&a[x].r<=r) {
(a[x].lazy+=c)%=mod,(a[x].sum+=len(x)*c)%=mod;
return;
}
down(x);
LL mid=a[x].l+a[x].r>>1;
if(mid>=l) {
update(l,r,c,a[x].ls);
}
if(mid<r) {
update(l,r,c,a[x].rs);
}
up(x);
}
LL query(LL l,LL r,LL x) {
if(a[x].l>=l&&a[x].r<=r) {
return a[x].sum;
}
down(x);
LL mid=a[x].l+a[x].r>>1,tot=0;
if(mid>=l) {
tot+=query(l,r,a[x].ls);
}
if(mid<r) {
tot+=query(l,r,a[x].rs);
}
return tot%mod;
}
inline LL sum(LL x,LL y) {
LL ret=0;
while(top[x]!=top[y]) {
if(d[top[x]]<d[top[y]]) {
swap(x,y);
}
ret=(ret+query(id[top[x]],id[x],rt))%mod;
x=f[top[x]];
}
if(id[x]>id[y]) {
swap(x,y);
}
return (ret+query(id[x],id[y],rt))%mod;
}
inline void updates(LL x,LL y,LL c) {
while(top[x]!=top[y]) {
if(d[top[x]]<d[top[y]]) {
swap(x,y);
}
update(id[top[x]],id[x],c,rt);
x=f[top[x]];
}
if(id[x]>id[y]) {
swap(x,y);
}
update(id[x],id[y],c,rt);
}
int main() {
scanf("%lld %lld %lld %lld",&n,&m,&r,&mod);
for(LL i=1; i<=n; i++) {
scanf("%lld",v+i);
}
for(LL x,y,i=1; i<n; i++) {
scanf("%lld %lld",&x,&y);
add(x,y),add(y,x);
}
cnt=0,dfs1(r),dfs2(r,r),cnt=0,build(1,n,rt=cnt++);
for(LL op,x,y,k,i=1; i<=m; i++) {
scanf("%lld",&op);
if(op==1) {
scanf("%lld %lld %lld",&x,&y,&k);
updates(x,y,k);
} else if(op==2) {
scanf("%lld %lld",&x,&y);
printf("%lld
",sum(x,y));
} else if(op==3) {
scanf("%lld %lld",&x,&y);
update(id[x],id[x]+size[x]-1,y,rt);
} else {
scanf("%lld",&x);
printf("%lld
",query(id[x],id[x]+size[x]-1,rt));
}
}
return 0;
}