AT1761 square1001の通学経路 (square1001's School Road)
問題文
square1001は、毎日歩いて中学校まで通っている。
彼は、左下の交差点 (1,1) に住んでおり、 右上の交差点 (W,H)にある学校まで行く。
ただし、次のような条件がある。
彼は時間短縮のために右か上にしか進まない。
彼はその日、K 個のマスに用事があった。
左下 が(Xi,Yi) で, 右上が(Xi+1,Yi+1) のマスである。
そのため、用事のあるマスそれぞれについて、その周りの交差点4つのうち少なくとも1つは通る必要があった。
それらの条件を満たす行き方は何通りあるか。 mod 1,000,000,007で求めよ。
入力例1
4 4 1
2 2
出力例1
18
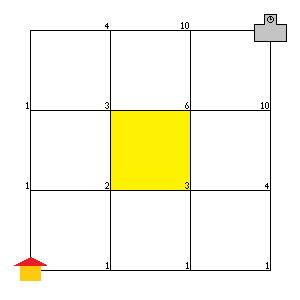
(1,1)→(1,2)→(1,3)→(1,4)→(2,4)→(3,4)→(4,4)という行き方と、
(1,1)→(2,1)→(3,1)→(4,1)→(4,2)→(4,3)→(4,4)という行き方はできない。
よって, 20−2=18を出力する。
※図の左上数が抜けていてすみません。
题意翻译
square1001每天步行到学校。
他住在左下方的十字路口(1,1),去位于右上角(W,H)的学校。
但是,有一些条件。
他为了缩短时间只能往右或上走。 那天,他找了有K个格子,左下角坐标分别为(Xi1,Yi1),(Xi2,Yi2),(Xi3,Yi3) ......(XiK,YiK)
而且,对于这种的格子,其周围的4个格子(指周围四个格子中四个顶点坐标中的一个)中square1001至少需要经过1个。
满足这些条件的路径有多少条?
答案mod 1,000,000,007后输出 。
怎么做呢?
这种题直接考虑DP计数就好了。
有一个比较类似的题建议做一下。
CF559C Gerald and Giant Chess
这道题的转移:对于每一个点,可以直接由它的左下加右下转移过来。至于限制条件怎么走,我们发现对于每一个方块,必行的两个点的横坐标加纵坐标是一定的,因此可以维护一个数组,当且仅当它与地图上记录的点的信息对应时进行转移。
//记录点的信息
++mp[x + 1][y];++mp[x][y + 1];
//对每个横纵坐标的合维护出现次数
++cnt[x + y + 1];
//转移时进行判断
cnt[i + j] == mp[i][j]
拿样例进行说明,例如在(1,4)点时(是非法状态不能转移),由于cnt[5] = 1,mp[1][4] = 0,不能进行转移。由此保证路径一定经过必过的点。
这个是我看了snow39的代码发现的好技巧。
代码
#include <bits/stdc++.h>
namespace fdata
{
inline char nextchar()
{
static const int BS = 1 << 21;
static char buf[BS], *st, *ed;
if (st == ed)
ed = buf + fread(st = buf, 1, BS, stdin);
return st == ed ? -1 : *st++;
}
#ifdef lky233
#define nextchar getchar
#endif
template <typename Y>
inline void poread(Y &ret)
{
ret = 0;
char ch;
while (!isdigit(ch = nextchar()))
;
do
ret = ret * 10 + ch - '0';
while (isdigit(ch = nextchar()));
}
#undef nextcar
} // namespace fdata
using fdata::poread;
using namespace std;
const int MAXN = 1005;
const int MOD = 1e9 + 7;
int f[MAXN][MAXN];
int mp[MAXN][MAXN];
int cnt[MAXN];
int h, w, k;
int main()
{
poread(h), poread(w), poread(k);
for (register int i = 1, x, y; i <= k; ++i)
{
poread(x), poread(y);
++mp[x + 1][y];
++mp[x][y + 1];
++cnt[x + y + 1];
}
f[1][1] = 1;
for (register int i = 1; i <= h; ++i)
{
for (register int j = 1; j <= w; ++j)
{
if (i != 1 && cnt[i + j] == mp[i][j])
f[i][j] = (f[i][j] + f[i - 1][j]) % MOD;
if (j != 1 && cnt[i + j] == mp[i][j])
f[i][j] = (f[i][j] + f[i][j - 1]) % MOD;
}
}
cout << f[h][w] << endl;
}
我在看的时候看到了一份python代码,于是搬过来了。
来源提交记录
from collections import defaultdict,deque
import sys,heapq,bisect,math,itertools,string,queue,datetime,random
sys.setrecursionlimit(10**8)
INF = float('inf')
mod = 10**9+7
eps = 10**-7
def inpl(): return list(map(int, input().split()))
def inpls(): return list(input().split())
H,W,K = inpl()
XYs = [inpl() for _ in range(K)]
XYs.sort()
MAX = H+W
fac = [1]*(MAX+1)
for i in range(1,MAX+1):
fac[i] = (fac[i-1]*i)%mod
gyakugen = [1]*(MAX+1)
gyakugen[MAX] = pow(fac[MAX],mod-2,mod)
for i in range(MAX,0,-1):
gyakugen[i-1] = (gyakugen[i]*i)%mod
def Comb (n,k):#nCk
return (fac[n]*gyakugen[k]*gyakugen[n-k])%mod
def calc(xys,xyt):
dx = xyt[0] - xys[0]
dy = xyt[1] - xys[1]
return Comb(dx+dy,dx)
def LU(xy):
x,y = xy
return([x,y+1])
def RD(xy):
x,y = xy
return([x+1,y])
tmp0 = calc([1,1],LU(XYs[0]))
tmp1 = calc([1,1],RD(XYs[0]))
for i in range(1,K):
tmp0ed,tmp1ed = tmp0,tmp1
tmp0 = tmp0ed * calc(LU(XYs[i-1]),LU(XYs[i])) + tmp1ed * calc(RD(XYs[i-1]),LU(XYs[i]))
tmp1 = tmp0ed * calc(LU(XYs[i-1]),RD(XYs[i])) + tmp1ed * calc(RD(XYs[i-1]),RD(XYs[i]))
tmp0 %= mod
tmp1 %= mod
ans = tmp0 * calc(LU(XYs[K-1]),[W,H]) + tmp1 * calc(RD(XYs[K-1]),[W,H])
print(ans%mod)