两个矩阵A, B需要计算A的每一行和B的每一行之间的距离。返回矩阵为distance_matrix.
相关参考:https://stackoverflow.com/questions/28687321/computing-euclidean-distance-for-numpy-in-python?answertab=votes#tab-top
https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.cdist.html
distance_matrix[i,j] = ||$a_i - b_j $ || = $sqrt{(a_i-b_j)^T(a_i-b_j) }$。
1.用A[:,None - B]得到:
A = np.arange(25).reshape(5, 5) B = np.ones((2,5)) B[1, :] = 2
print A: 得到:

print B:

vectors_diff = A[:, None] - B print(vectors_diff.shape) # Shape of vectors_diff is (5, 2, 5)
print vectors_diff: 有:
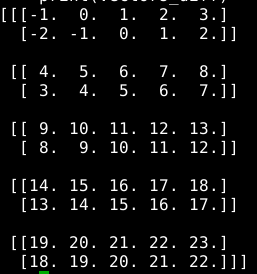
然后可以用 np.linalg.norm(x, ord=None, axis=2, keepdims=True) 计算二范数。Shape为: (5,2,1)
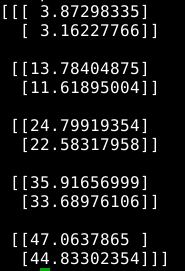
2. 方法2:
两个向量$x= [x_1,x_2,x_3]^T$ 和$y = [y_1,y_2,y_3]^T$,我们需要计算 $(x_1-y_1)^2 + (x_2-y_2)^2 + (x_3-y_3)^2$:
即:
$y_1^2 + x_1 ^ 2 -2x_1y_1+y_2^2+x_2^2-2x_2y_2+ x_3^2+y_3^2-2x_3y_3$.
重新写得到:
$sum(x_i)^2 + sum(y_i)^2 -2*sum x_iy_i$
sum_squares_A = np.sum(A**2, axis=1) sum_squares_B = np.sum(B**2, axis=1) xy_products = A.dot(B.T) sum_squares = sum_squares_A + sum_squares_B[:, None]