luogu题解 CF522D Closest Equals

写在前面

注：因为变量名中有下划线，所以有些地方使用的是代码块而没有使用 \(\text{LateX}\) 渲染，恳请管理大大原谅。

转了一圈题解发现没有用莫队的？

唯一一个涉及到的貌似还被卡了？

那么我就来一发回滚莫队吧。

题面：CF522D Closest Equals

Solution

一开始把题目读错了，以为求的是一段区间内最远的两个相同的数的距离，

这不就回滚莫队板子嘛。

调半天发现是求最近的两个相同的数的距离，想想怎么用莫队维护。

跟着回滚莫队的做法，先进行离散化、分块、排序这一类基本操作。

然后每次轮到一个新块时，我们不是要移动两端点到块的右端嘛。

我们要查询的区间因此就分成了两块，暂且称作左块和右块。

题目要求是求最近的，那么只需统计相邻的两个相同的数的贡献。

开四个数组 cntr[x], cntr_pre[x], cntl_t[x], cntl_pre_t[x]，分别表示一个数 \(x\) 在右块的最小的位置，\(x\) 在右块中上一次出现的位置，\(x\) 在左块中的最大位置，\(x\) 在左块中上一次出现的位置。

画成图大体是这个样子：

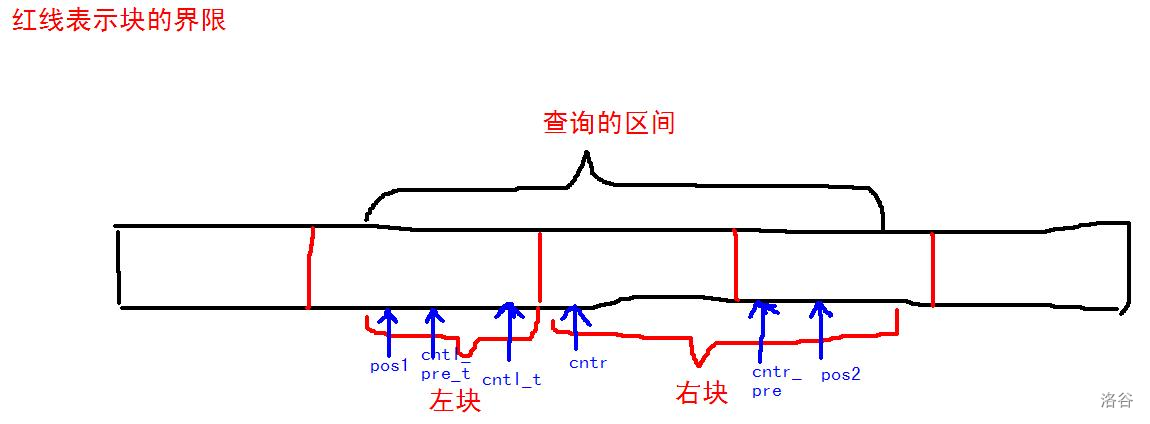
假设图中标记的都是一个数：

• 如果在左块中又枚举到一个数 \(pos_1\)，它对答案的贡献显然是 cntl_pre_t - pos1。
• 如果在右块中又枚举到一个数 \(pos_2\)，它对答案的贡献显然是
  pos2 - cntr_pre。
• 因为左块和右块之间可能也会有贡献，所以还需要统计 cntr - cntl_t。

一些小细节：

• 注意没有相同的数时要输出 \(-1\)；
• 在左块或者右块中统计答案时，如果其中某一个值不存在就不要统计答案了。

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 5e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

struct Ques{
    int l, r, bh;
}q[MAXN];

int n, m; 
int L = 1, R = n, preL = 0, Ans, Res, _L;
int a[MAXN], date[MAXN], date_num = 0;
int lef[MAXN], rig[MAXN], bel[MAXN];
int cntr[MAXN], cntr_pre[MAXN], cntl_t[MAXN], cntl_pre_t[MAXN];
int ans[MAXN];

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

bool cmp(Ques x, Ques y) { return bel[x.l] == bel[y.l] ? x.r < y.r : x.l < y.l; } //按块排序 

void Init() {
    n = read(), m = read();
    for(int i = 1; i <= n; ++i) a[i] = date[i] = read();
    sort(date + 1, date + n + 1); date[0] = -INF; //离散化 
    for(int i = 1; i <= n; ++i) if(date[i] != date[i - 1]) date[++date_num] = date[i];
    for(int i = 1; i <= n; ++i) a[i] = lower_bound(date + 1, date + date_num + 1, a[i]) - date;
    for(int i = 1; i <= date_num; ++i) cntr[i] = cntr_pre[i] = ans[i] = INF; 
    for(int i = date_num + 1; i <= m; ++i) ans[i] = INF; //初始化为极大值 
    
    int len = sqrt(n + 0.5);//分块 
    int block_num = n / len;
    for(int i = 1; i <= block_num; ++i) lef[i] = rig[i - 1] + 1, rig[i] = rig[i - 1] + len; 
    if(rig[block_num] < n) {
        ++ block_num;
        lef[block_num] = rig[block_num - 1] + 1;
        rig[block_num] = n;
    }
    for(int i = 1; i <= block_num; ++i) 
        for(int j = lef[i]; j <= rig[i]; ++j) 
            bel[j] = i;
}

void Add(int pos, int &ans_) {
    int x = a[pos];
    cntr[x] = min(cntr[x], pos); //更新右块中x的最小的位置
    if(cntr_pre[x] != INF) ans_ = min(ans_, pos - cntr_pre[x]); // 只有x在右块中出现过才统计答案
    cntr_pre[x] = pos; // 更新
}
void Add_tem(int pos, int &ans_, int type) {
    int x = a[pos];
    cntl_t[x] = max(cntl_t[x], pos); // 更新左块中x的最大位置
    if(cntl_pre_t[x]) ans_ = min(ans_, cntl_pre_t[x] - pos); //只有x在左块中出现过才统计答案
    cntl_pre_t[x] = pos; //更新
    if(cntr[x] != INF && cntl_t[x] && type) ans_ = min(ans_, cntr[x] - cntl_t[x]); //统计左右块之间的贡献
}

void Del(int pos) { cntr[a[pos]] = cntr_pre[a[pos]] = INF; }
void Del_tem(int pos) { cntl_t[a[pos]] = cntl_pre_t[a[pos]] = 0; }

int main()
{
    Init();
    for(int i = 1; i <= m; ++i) q[i].l = read(), q[i].r = read(), q[i].bh = i;
    sort(q + 1, q + m + 1, cmp);
    for(int i = 1; i <= m; ++i) { //回滚莫队基操？
        if(preL != bel[q[i].l]) {
            while(R > rig[bel[q[i].l]]) Del(R--);
            while(L <= rig[bel[q[i].l]]) Del(L++);
            Ans = INF, R = rig[bel[q[i].l]], preL = bel[q[i].l];
        }
        if(bel[q[i].l] == bel[q[i].r]) {
            for(int j = q[i].r; j >= q[i].l; --j) Add_tem(j, ans[q[i].bh], 0); //倒序枚举方便统计答案 
            for(int j = q[i].r; j >= q[i].l; --j) Del_tem(j);
        } else {
            while(R < q[i].r) Add(++R, Ans);
            _L = L, Res = Ans;
            while(_L > q[i].l) Add_tem(--_L, Res, 1);
            ans[q[i].bh] = Res;
            while(_L < L) Del_tem(_L++);
        }
    }
    for(int i = 1; i <= m; ++i) printf("%d\n", ans[i] == INF ? -1 : ans[i]);
    return 0;
}