前言
昨天简单学习了第一章,对应于视频中的第一集。然后今天(以及昨天的部分时间)学习了第二章的内容,对应于视频的2,3,4集。主要是介绍了信息的表示与处理,关于表示,主要描述了信息在计算机中的存储细节,关于处理,主要是计算机中最重要的三种数字表示:无符号编码,补码编码以及浮点数编码。
信息存储
现代计算机存储和处理的信息是以二值信号表示的,是基于二进制进行编码的,好处在于:1. 比如我们可以将低电压表示0,将高电压表示1,如果电路中存在噪音或不完善的地方,只要不超过你设定的阈值,你就会得到一个清晰的信号;2. 对于信息存储而言,存储一位信息或一个数字值比存储一个模拟值更容易。

这些微不足道的二进制数字,或者被称为位。孤立来讲,单个的位不是非常有用,然而把位组合起来,再加上某种解释,即赋予不同的可能位模式以含义,我们便可以表示任何有限集合的元素。也就是说,我们在计算机中用比特位来表示所有的数字。
大多数计算机使用8位的块,称为字节,作为最小的可寻址的内存单元,而不是访问内存单独的位。每台计算机都有一个字长,指明指针数据的标称大小。字长定义了操作系统通常处理多大的值和算数运算,并且指针和地址大小也是字长确定的。这个也就是32位机器(字长为32位)和64位机器(字长为64位)的区别之一。
内存是一系列字节,我们可以根据字长将其划分成不同的字(Word),每个字的地址是该字中最低位的地址。主要思想是,我们可以把任意多的字节组合起来称之为一个字。
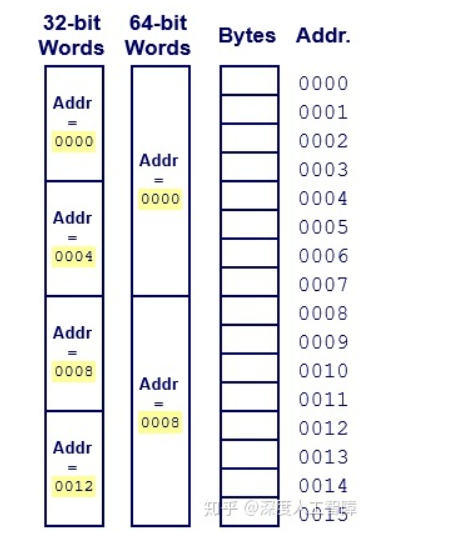
现在大部分机器是32位字长或者64位字长的,而程序可以通过不同的编译指令将其编译成32位程序或者64位程序(程序的字长是由编译决定的),其中32位机器可以运行32位程序,但是不能运行64位程序,而64位机器可以运行32位程序和64位程序。并且32位程序和64位程序对C数据类型的典型大小也有影响,具体可以看看这篇文章
字节顺序
由于一个字是由多个字节组成的,所以里面的字节排序顺便有两种。分别是大端和小端。

C语言的几个基本运算
C语言中的位级运算
C语言的一个很有用的特性就是支持按位布尔运算。|表示OR、&表示AND、~表示NOT、^表示XOR。
这种运算可以运用于任何"整型"的数据类型上,如下图例子:

C语言中的逻辑运算
C语言还提供了一组逻辑运算符,||、&&和!。要注意逻辑运算和位级运算的区别,在逻辑运算中,只要是非零的数据就表示为TRUE,全零的数据就表示为FALSE,所以计算时候先将其转换为TRUE和FALSE,然后计算出来的结果只会是0x00或0x01,分别对应FALSE和TRUE。
其中,逻辑运算还有一个提前终止特性。
移位运算
对于左移,没有区分,移位后的低位都用0来填充。
对于右移,分为逻辑右移和算术右移。对于逻辑右移,移位后左端的高位用0来填充,对于算术右移,移位后的高位用最高有效位填充。
整数表示
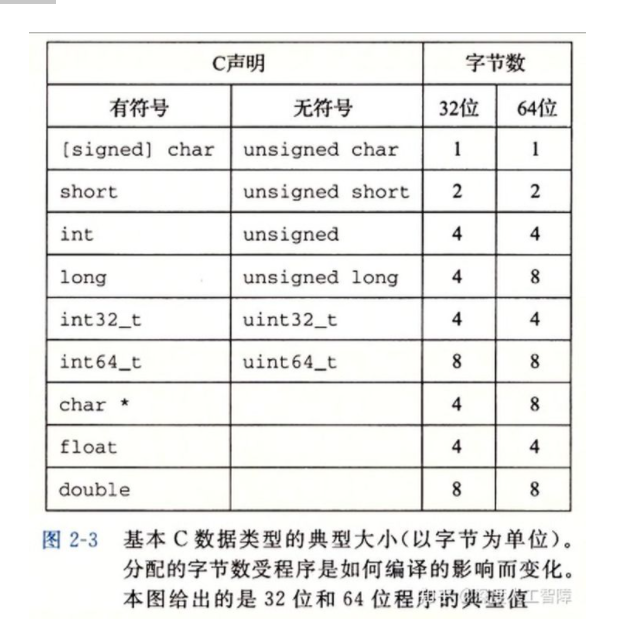
C语言提供了多种由不同字节数目构成的、具有不同范围的整型数据类型,并且每种整型数据类型都有有符号(signed)和无符号(unsigned)两个版本,常量默认是有符号版本,可以加上后缀u或者U来将其指定为无符号版本。
C和C++都支持有符号和无符号数,而Java只支持有符号数。
对于这些整型数据类型,C语言具有一个标准定义,而标准定义,32位的实际取值范围,64位的实际取值范围都有差异。
无符号数的编码
其实这里就是没有最高符号位,将最高位一起用求和公式求和即可。
补码编码
这个主要是对于上面整型数据中的有符号数。
主要就是最高位做符号位,对应的计算公式为:
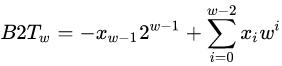
有符号数和无符号数之间的转换
C语言允许在各种不同的数字数据类型之间做强制类型转换。
对于大多数C语言的实现,处理同样字长的有符号数和无符号数之间相互转换的一般规则是:数值可能会改变,但位模式不变。意思是,01串不变,只是改变了解释这些位的方式。
补码变无符号数
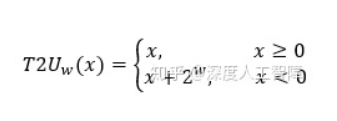
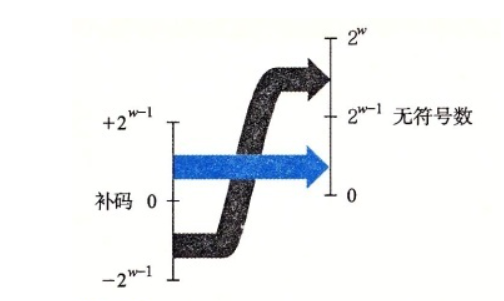
无符号数变补码
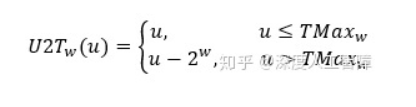
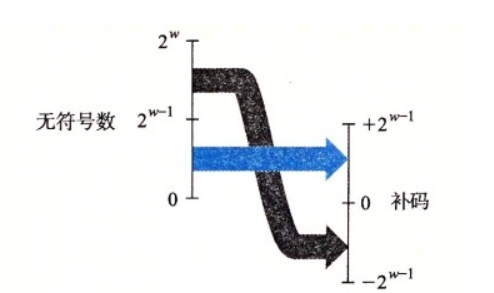
注意:在C语言中,当一个有符号数和一个无符号数进行计算时,会隐式地将有符号数转化为无符号数。
不同字长的类型转换
在不同字长的整数之间进行类型转换,要保持在数据类型范围内的数值是不变的。以下有两种情况:从较短字长的数据类型转换到较长字长的数据类型,比如short到int,就需要进行扩展位;从较长字长的数据类型转换到较短字长的数据类型,比如int到short,就需要截断位。
扩展数字
要将一个无符号数转换为一个更大的数据类型,我们只需要简单地在表示地开头添加零。称为零扩展。
要将一个补码数字转换为一个更大数据类型,可以执行为符号扩展,在表示中添加最高有效位的值。
注意:当把short转换为unsigned int的时候,我们要先改变大小,之后再完成从有符号到无符号的转换,这个由C语言规定。
截断数字
对于无符号数,定义宽度为w的位向量和宽度为w'的位向量,其中将w的位向量抓换为w'的位向量,将比w'高的位直接丢弃,这会改变数的值,也是溢出的一种形式。其实就是mod然后取余的操作。
补码也有相似的属性,只不过把最高位转化为符号位。有符号(补码编码)的截断,我们只需要多加一步,将无符号编码转换为补码编码就可以了。
整数运算
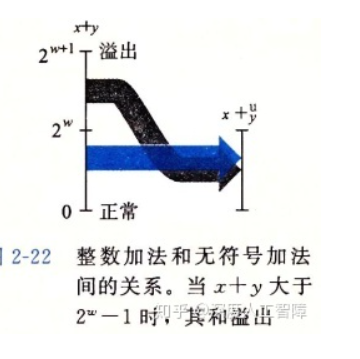
无符号数加法
主要分为正常和溢出两种情况,正常的话其两个无符号数的和大于任意一个加数,而溢出时,其两数的和相当于将实际的和减去2**w,此时的和会比加数小(溢出的检测条件)
补码加法
补码加法中,使用和无符号数相同的位向量,可以保证在补码取值范围内计算正确,而和超过最大值称为正溢出,超过最小值称为负溢出。
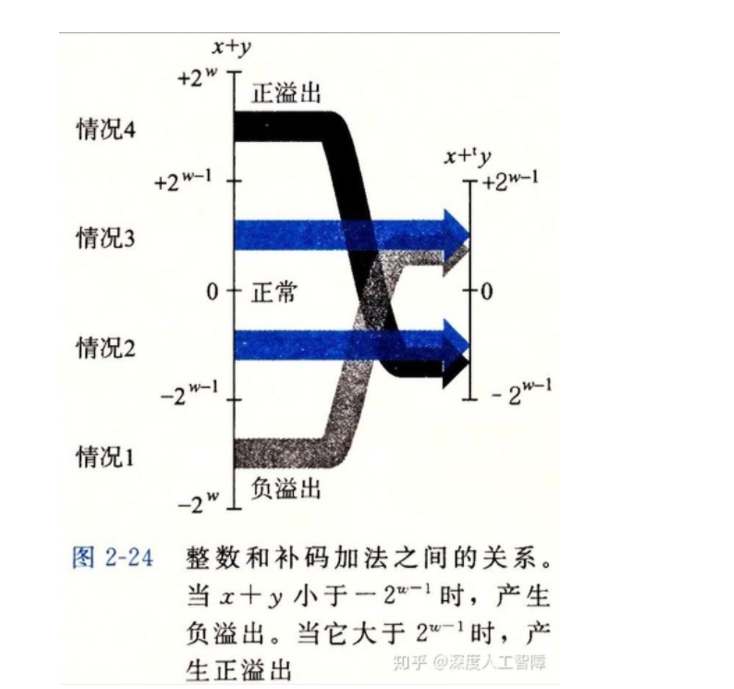
当产生正溢出时,将其和减去2 ** w,当其产生负溢出时,将其和加上2 ** w。
无符号乘法
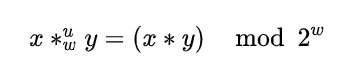
补码乘法

浮点数
浮点表示对形如V=x*(2 ** y)的有理数进行编码。它对执行涉及非常大的数字,非常接近于0的数字,以及更普遍地作为实数运算地近似值地计算,是很有用的。
浮点数实际上也是用二进制小数来表示。
IEEE浮点表示使用以下式子表示:
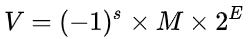
符号(Sign)s:用来确定V的正负性,当s=0时表示正数,s=1时表示负数。用一个单独的符号位直接进行编码。
尾数(Significand)M: 是一个二进制小数,通常介于1和2之间的小数。使用k位二进制进行编码的小数。
阶码(Exponent)E:对浮点数进行加权。使用n位进行编码的正数。
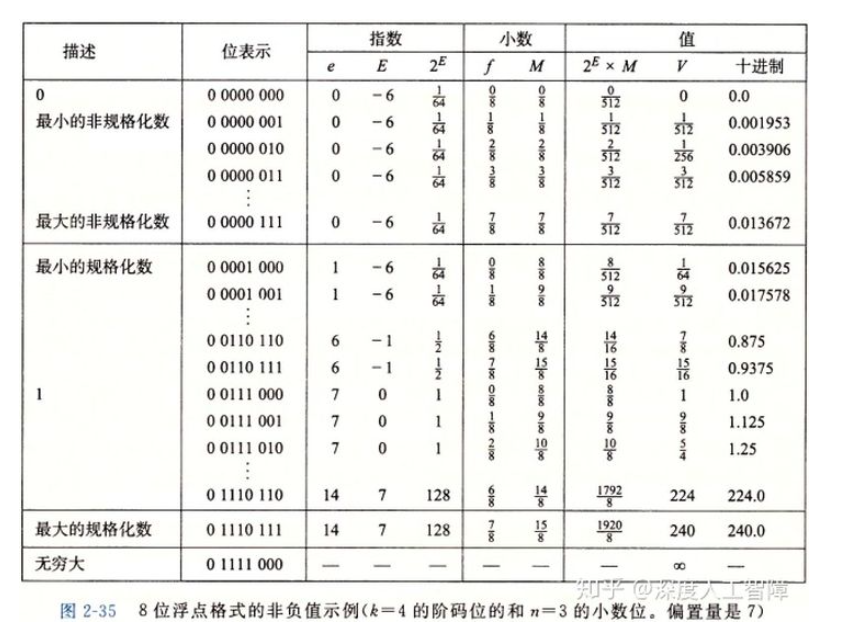
C语言中有单精度精浮点数float,其中s=1、k=8、n=23;还有双精度浮点数double,其中s=1、k=11、n=52。

根据exp的值,被编码的值可以分为三种不同的情况。
- 规格化的值
当exp的位模式既不全为0也不全为1,都属于这种情况。在这种情况下,阶码字段被解释为以偏置值形式表示的有符号数。也就是说,阶码的值E=e=Bias,其中e是无符号数,而Bias等于(2 ** k-1)-1的偏置值。小数字段被解释为描述小数值f,也就是二进制小数点在最高有效位的左边。尾数定义为M=1+f,也就是隐含的以1开头的表示。
2.非规格化的值
当阶码域全为0,所表示的数是非规格化形式。在这种情况下,阶码的值是E-1-bias,而尾数的值是M=f。
3.特殊值
当阶码全为1的时候出现。当小数域全为0时,得到的值表示无穷,当s等于0,表示正无穷,当s等于1时,表示负无穷。当小数域为非零时,结果值被称为“NAN”。
舍入
因为表示方法限制了浮点数的范围和精度,所以浮点运算只能近似地表示实数运算。这就是舍入运算的任务。
常见的舍入方法有四种:向零舍入、向上舍入、向下舍入以及向偶数舍入。以十进制为例可以看以下表格
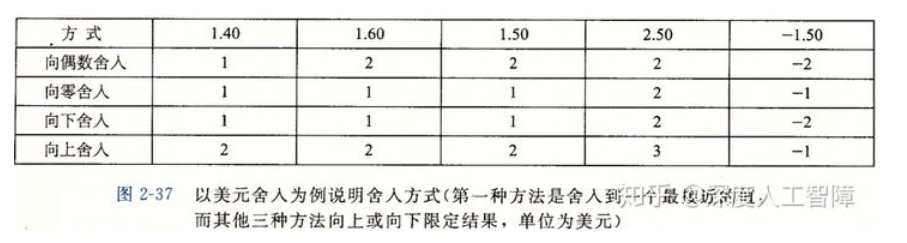
而二进制的中间值是 [公式] ,比如 [公式] 就比中间值大, [公式] 就比中间值小。而且二进制中,当最后一个有效位为0时,为偶数。比如
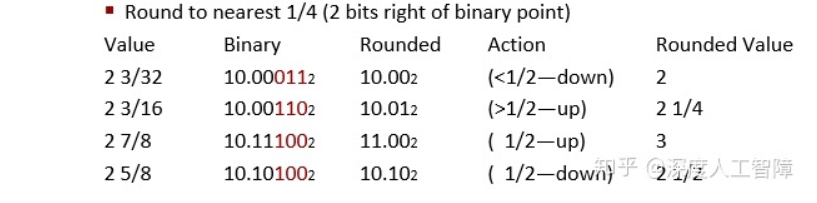
10.00011:由于011比中间值小,所以直接向下舍入,为10.00。
10.00110:由于110比中间值大,所以直接向上舍入,为10.01。
10.11100:由于100为中间值,而10.11最后一个有效位1位奇数,所以向上舍入为偶数11.00。
10.10100:由于100为中间值,而10.10最后一个有效位0位偶数,所以直接向下舍入10.10。