决策树 (Decision Tree)是在已知各种情况发生概率的基础上,通过构成 决策树 来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称 决策树 。在机器学习中,决策树 是一个预测模型,他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度,使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念,本文着重讲ID3算法。
假设存在如下一组信息:
| 天气 | 气温 | 湿度 | 风 | 外出 |
|---|---|---|---|---|
| 晴朗 | 高温 | 高 | 无风 | no |
| 晴朗 | 高温 | 高 | 有风 | no |
| 多云 | 高温 | 高 | 无风 | yes |
| 下雨 | 温暖 | 高 | 无风 | yes |
| 下雨 | 寒冷 | 正常 | 无风 | yes |
| 下雨 | 寒冷 | 正常 | 有风 | no |
| 多云 | 寒冷 | 正常 | 有风 | yes |
| 晴朗 | 温暖 | 高 | 无风 | no |
| 晴朗 | 寒冷 | 正常 | 无风 | yes |
| 下雨 | 温暖 | 正常 | 无风 | yes |
| 晴朗 | 温暖 | 正常 | 有风 | yes |
| 多云 | 温暖 | 高 | 有风 | yes |
| 多云 | 高温 | 正常 | 无风 | yes |
| 下雨 | 温暖 | 高 | 有风 | no |
假如时间发生发概率为(p1,p2,...,pn),那么可以定义信息熵为:
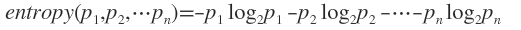
例如外出的概率是9/14,不外出的概率是5/14,那么 外出的信息熵entropy 为:
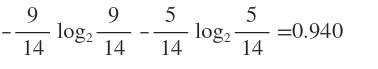
将上面的表格整理一下如下:
| 天气 | yes | no | 气温 | yes | no | 湿度 | yes | no | 风 | yes | no | 外出 | yes | no |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 晴朗 | 2 | 3 | 高温 | 2 | 2 | 高 | 3 | 4 | 无风 | 6 | 2 | 外出 | 9 | 5 |
| 多云 | 4 | 0 | 温暖 | 4 | 2 | 正常 | 6 | 1 | 有风 | 3 | 3 | |||
| 下雨 | 3 | 2 | 寒冷 | 3 | 1 |
各个天气情况 的信息熵计算为:
-
天气为晴朗时,2/5的概率外出,3/5的概率不外出,信息熵为0.971
-
天气为多云时,信息熵为0
-
天气为下雨时,3/5的概率外出,2/5的概率不外出,信息熵为0.971
而天气是 晴朗 的概率为5/14,天气是 多云 的概率为4/14,天气是 下雨 的概率为5/14,所以 天气 的信息熵为:
5/14 × 0.971 + 4/14 × 0 + 5/14 × 0.971 = 0.693
天气的 信息增益gain 为:
0.940-0.693=0.247
同理 温度gain 为0.029, 湿度gain 为0.152,风gain 为0.048
天气的信息熵下降得最快,所以决策树的根节点为 天气 ,子节点为 晴朗 、多云 、下雨 :
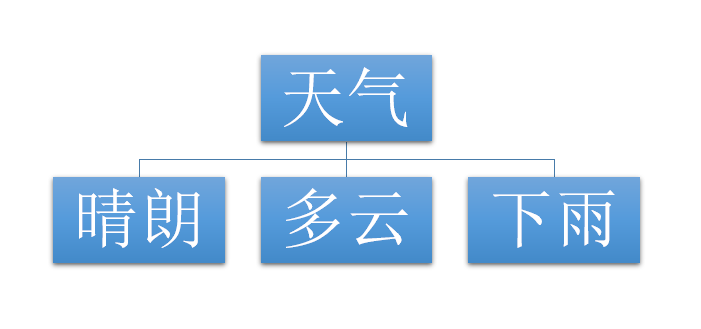
根据第一个表格得知,天气 晴朗 的日子有5天,这5天对应各种不一样的 气温 、 湿度 、 风 、 外出 ,如下:
晴朗 {'湿度': ['高', '高', '高', '正常', '正常'], '风': ['无风', '有风', '无风', '无风', '有风'], '气温': ['高温', '高温', '温暖', '寒冷', '温暖']}
下雨 {'湿度': ['高', '正常', '正常', '正常', '高'], '风': ['无风', '无风', '有风', '无风', '有风'], '气温': ['温暖', '寒冷', '寒冷', '温暖', '温暖']}
多云 {'湿度': ['高', '正常', '高', '正常'], '风': ['无风', '有风', '有风', '无风'], '气温': ['高温', '寒冷', '温暖', '高温']}
多云 ['yes', 'yes', 'yes', 'yes']
晴朗 ['no', 'no', 'no', 'yes', 'yes']
下雨 ['yes', 'yes', 'no', 'yes', 'no']
在前面计算,由于 多云 的信息熵为0,所以多云的时候是一定会外出的,即 多云=yes :
晴朗 {'湿度': ['高', '高', '高', '正常', '正常'], '风': ['无风', '有风', '无风', '无风', '有风'], '气温': ['高温', '高温', '温暖', '寒冷', '温暖']}
下雨 {'湿度': ['高', '正常', '正常', '正常', '高'], '风': ['无风', '无风', '有风', '无风', '有风'], '气温': ['温暖', '寒冷', '寒冷', '温暖', '温暖']}
多云 'yes'
多云 'yes'
晴朗 ['no', 'no', 'no', 'yes', 'yes']
下雨 ['yes', 'yes', 'no', 'yes', 'no']
此时需要再次计算:
- 晴朗条件下,湿度、风、气温那个的信息增益下降最快,选取下降最快的为晴朗的下一个节点
- 下雨条件下,湿度、风、气温那个的信息增益下降最快,选取下降最快的为下雨的下一个节点
- 再次判断哪一个信息熵变成了0,变成了0则可以终止这一条树
经过代码计算, 晴朗 的下一个节点为 湿度 , 下雨 的下一个节点为 风 ,以此继续递归下去.
python代码为
整理的原始数据为:
condition = {'风': ['无风', '有风', '无风', '无风', '无风', '有风', '有风', '无风', '无风', '无风', '有风', '有风', '无风', '有风'],
'湿度': ['高', '高', '高', '高', '正常', '正常', '正常', '高', '正常', '正常', '正常', '高', '正常', '高'],
'天气': ['晴朗', '晴朗', '多云', '下雨', '下雨', '下雨', '多云', '晴朗', '晴朗', '下雨', '晴朗', '多云', '多云', '下雨'],
'气温': ['高温', '高温', '高温', '温暖', '寒冷', '寒冷', '寒冷', '温暖', '寒冷', '温暖', '温暖', '温暖', '高温', '温暖']}
result = {'外出': ['no', 'no', 'yes', 'yes', 'yes', 'no', 'yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']}
计算各种情况出现的概率:
# 计算出现的概率
def CalcProbability(array):
dict = {}
count = Counter(array)
for item in count:
dict[item] = count[item] / len(array)
return dict
计算信息熵:
# 计算信息熵
def CalcEntropy(array):
entropy = 0
for i in range(0, len(array)):
entropy = entropy + (-array[i] * math.log2(array[i]))
return entropy
将原数据变为这样的样式:
| 天气 | yes | no | 气温 | yes | no | 湿度 | yes | no | 风 | yes | no | 外出 | yes | no |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 晴朗 | 2 | 3 | 高温 | 2 | 2 | 高 | 3 | 4 | 无风 | 6 | 2 | 外出 | 9 | 5 |
| 多云 | 4 | 0 | 温暖 | 4 | 2 | 正常 | 6 | 1 | 有风 | 3 | 3 | |||
| 下雨 | 3 | 2 | 寒冷 | 3 | 1 |
# 重新整理数据
def Statistics(condition, result):
# 获得各种结果出现的概率
for k in result:
resultProbability = CalcProbability(result[k])
# {'no': 0.35714285714285715, 'yes': 0.6428571428571429}
# 获得结果的信息熵
resultarr = []
for key in resultProbability:
resultarr.append(resultProbability[key])
resultEntropy = CalcEntropy(resultarr)
# print(resultEntropy)
# 0.9402859586706311
# 统计各个条件下的外出结果
dict = {}
for key in condition.keys():
tempdict = {}
for i in range(0, len(condition[key])):
if condition[key][i] in tempdict:
for k in result:
tempdict[condition[key][i]].append(result[k][i])
else:
arr = []
for k in result:
arr.append(result[k][i])
tempdict[condition[key][i]] = arr
dict[key] = tempdict
# print(dict)
# {'风': {'有风': ['no', 'no', 'yes', 'yes', 'yes', 'no'], '无风': ['no', 'yes', 'yes', 'yes', 'no', 'yes', 'yes', 'yes']}, '湿度': {'正常': ['yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes'], '高': ['no', 'no', 'yes', 'yes', 'no', 'yes', 'no']}, '天气': {'晴朗': ['no', 'no', 'no', 'yes', 'yes'], '下雨': ['yes', 'yes', 'no', 'yes', 'no'], '多云': ['yes', 'yes', 'yes', 'yes']}, '气温': {'温暖': ['yes', 'no', 'yes', 'yes', 'yes', 'no'], '寒冷': ['yes', 'no', 'yes', 'yes'], '高温': ['no', 'no', 'yes', 'yes']}}
# 计算不同外出情况下的信息熵
newdict = {}
for keys in dict:
tempdict = {}
for key in dict[keys]:
temp = CalcProbability(dict[keys][key])
temparr = []
for value in temp:
temparr.append(temp[value])
tempdict[key] = CalcEntropy(temparr)
newdict[keys] = tempdict
# print(newdict)
# {'风': {'无风': 0.8112781244591328, '有风': 1.0}, '天气': {'多云': 0.0, '晴朗': 0.9709505944546686, '下雨': 0.9709505944546686}, '湿度': {'高': 0.9852281360342516, '正常': 0.5916727785823275}, '气温': {'温暖': 0.9182958340544896, '寒冷': 0.8112781244591328, '高温': 1.0}}
# 不同条件出现的概率
conditiondict = {}
for item in condition:
conditiondict[item] = CalcProbability(condition[item])
# print(conditiondict)
# {'气温': {'高温': 0.2857142857142857, '温暖': 0.42857142857142855, '寒冷': 0.2857142857142857}, '风': {'有风': 0.42857142857142855, '无风': 0.5714285714285714}, '湿度': {'高': 0.5, '正常': 0.5}, '天气': {'晴朗': 0.35714285714285715, '下雨': 0.35714285714285715, '多云': 0.2857142857142857}}
return resultEntropy, newdict, conditiondict
计算信息增益:
# 计算信息增益
def CalcGain(resultEntropy, conditionEntropy, conditionProbability):
conditionGain = {}
for keys in conditionEntropy:
number = 0
for key in conditionEntropy[keys]:
number = number + conditionEntropy[keys][key] * conditionProbability[keys][key]
conditionGain[keys] = resultEntropy - number
# reverse=True值按照从大到小排序
conditionGain = sorted(conditionGain.items(), key=lambda d: d[1], reverse=True)
return conditionGain
最终递归:
# 递归计算咯
def recursion(condition, result):
resultEntropy, conditionEntropy, conditionProbability = Statistics(condition, result)
# print(resultEntropy)
# print(conditionEntropy)
# print(conditionProbability)
conditionGain = CalcGain(resultEntropy, conditionEntropy, conditionProbability)
# print(conditionGain)
# 哦按段是否为零
key = conditionGain[0][0]
value = ""
for values in conditionEntropy[key]:
if conditionEntropy[key][values] == 0:
value = values
kinds = []
for item in condition[key]:
if item in kinds:
pass
else:
kinds.append(item)
# ['晴朗', '多云', '下雨']
# 删除天气这个key
arrcondition = condition[key]
condition.pop(key)
# print("sssssssss",key)
newcondition = {}
newresult = {}
for item in kinds:
dict = {}
resultarr = []
for i in range(0, len(arrcondition)):
if arrcondition[i] == item:
for keys in condition:
if keys in dict:
dict[keys].append(condition[keys][i])
else:
temparr = []
temparr.append(condition[keys][i])
dict[keys] = temparr
for key in result:
resultarr.append(result[key][i])
newresult[item] = resultarr
newcondition[item] = dict
# print(newcondition)
# {'多云': {'气温': ['高温', '寒冷', '温暖', '高温'], '风': ['无风', '有风', '有风', '无风'], '湿度': ['高', '正常', '高', '正常']}, '晴朗': {'气温': ['高温', '高温', '温暖', '寒冷', '温暖'], '风': ['无风', '有风', '无风', '无风', '有风'], '湿度': ['高', '高', '高', '正常', '正常']}, '下雨': {'气温': ['温暖', '寒冷', '寒冷', '温暖', '温暖'], '风': ['无风', '无风', '有风', '无风', '有风'], '湿度': ['高', '正常', '正常', '正常', '高']}}
# print(newresult)
# {'多云': ['yes', 'yes', 'yes', 'yes'], '晴朗': ['no', 'no', 'no', 'yes', 'yes'], '下雨': ['yes', 'yes', 'no', 'yes', 'no']}
if value in newcondition:
newcondition[value] = "yes"
# 得到的新condition为dict:
# '多云': 'yes'
# 下雨 {'风': ['无风', '无风', '有风', '无风', '有风'], '湿度': ['高', '正常', '正常', '正常', '高'], '气温': ['温暖', '寒冷', '寒冷', '温暖', '温暖']}
# 晴朗 {'风': ['无风', '有风', '无风', '无风', '有风'], '湿度': ['高', '高', '高', '正常', '正常'], '气温': ['高温', '高温', '温暖', '寒冷', '温暖']}
# 得到的新result为newresult:
# 多云 ['yes', 'yes', 'yes', 'yes']
# 晴朗 ['no', 'no', 'no', 'yes', 'yes']
# 下雨 ['yes', 'yes', 'no', 'yes', 'no']
print(newcondition)
tempresult = {}
for key in newcondition:
if key == value:
pass
else:
tempresult[key] = newresult[key]
recursion(newcondition[key], tempresult)
源码在我的博客上面: