Codeforces Round #549 (Div. 1)
传送门:
https://codeforces.com/contest/1142
A
分类讨论。
我们记出发点为 (s),走一步后(距离为 (L))到达的点为 (t)。
我们根据 (s,t) 的位置分成四种((2 imes2))情况:
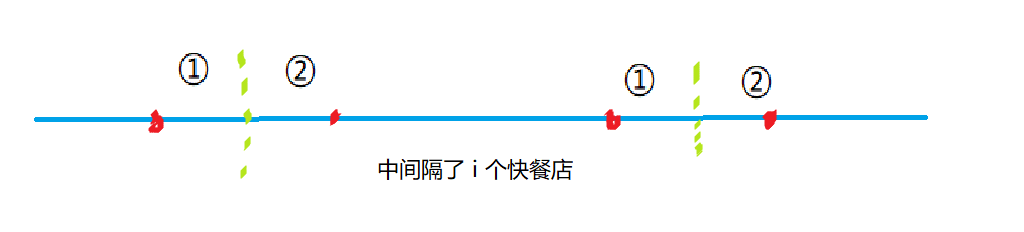
-
(s,t) 分别在 ①,①,此时 (L = b-a+ik)。
-
(s,t) 分别在 ①,②,此时 (L = (k-b)-a+ik)。
-
(s,t) 分别在 ②,①,此时 (L = b-(k-a)+ik)。
-
(s,t) 分别在 ②,②,此时 (L = (k-b)-(k-a)+ik)。
求出 (L) 后,我们只需求出当前 (L) 所对应的圈数 (res),用 (res) 更新 (x,y) 即可。
也就是对于 (uL = vnk),我们要找到最小的 (u),这个 (u) 便是 (res)。
这是经典的 (AX = BY) 形式的式子,有 (X = frac{B}{gcd(A, B)}),故 (res = frac{nk}{gcd(L, nk)})
// Problem: A. The Beatles
// Contest: Codeforces - Codeforces Round #549 (Div. 1)
// URL: https://codeforces.com/contest/1142/problem/A
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#pragma GCC optimize("O3")
#include<bits/stdc++.h>
using namespace std;
#define endl '
'
#define debug(x) cerr << #x << ": " << x << endl
#define pb push_back
#define eb emplace_back
#define set0(a) memset(a,0,sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define dwn(i,a,b) for(int i=(a);i>=(b);i--)
#define ceil(a,b) (a+(b-1))/(b)
#define all(x) (x).begin(), (x).end()
#define SUM(a) accumulate(all(a), 0LL)
#define MIN(a) (*min_element(all(a)))
#define MAX(a) (*max_element(all(a)))
#define lb(a, x) distance(begin(a), lower_bound(all(a), (x)))
#define ub(a, x) distance(begin(a), upper_bound(all(a), (x)))
#define INF 0x3f3f3f3f
#define ll_INF 0x7f7f7f7f7f7f7f7f
using pii = pair<int, int>;
using pdd = pair<double, double>;
using vi = vector<int>;
using vvi = vector<vi>;
using vb = vector<bool>;
using vpii = vector<pii>;
using ll = long long;
using ull = unsigned long long;
inline void read(int &x) {
int s=0;x=1;
char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-')x=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
x*=s;
}
#define int long long
int x, y;
int n, k, a, b;
int gcd(int a, int b){
return b? gcd(b, a%b): a;
}
void get(int L){
if(L<0) L+=n*k;
int res=n*k/gcd(L, n*k);
x=max(x, res), y=min(y, res);
}
signed main(){
cin>>n>>k>>a>>b;
x=0, y=ll_INF;
rep(i,0,n-1){
int L;
L=b-a+i*k;
get(L);
L=(k-b)-a+i*k;
get(L);
L=b-(k-a)+i*k;
get(L);
L=(k-b)-(k-a)+i*k;
get(L);
}
cout<<y<<' '<<x<<endl;
return 0;
}
B
倍增。
题目查询子段 ([l, r]) 是否存在子序列是循环移位。
记 (i) 点为长为 (n) 的一个循环移位的末位,我们知道,从 (i) 点向前跳 (n-1) 次它所对应的前驱就可以找到开头。
例如对于
1 2 3所构成的所有循环移位,1的前驱是3,2的前驱是1,3的前驱是2。
结合贪心的思想,上面的查询可进一步转化为:对于子段 ([l, r]),是否存在一个作为循环移位末位的点 (i),使得其向前跳 (每一次都是找最近的前驱)(n-1) 次所到达的开头点仍处于 ([l, r]) 中。
-
一个点向前跳 (n-1) 次,我们可以用倍增来处理。
-
而上述的判断跳 (n-1) 次能否在 ([l, r]) 则可以用 ST 表来处理,维护的信息是 ([l, r]) 对应的每个点向前跳 (n-1) 次能到达的下标最大的位置。
// Problem: B. Lynyrd Skynyrd
// Contest: Codeforces - Codeforces Round #549 (Div. 1)
// URL: https://codeforces.com/problemset/problem/1142/B
// Memory Limit: 256 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#pragma GCC optimize("O3")
#include<bits/stdc++.h>
using namespace std;
#define endl '
'
#define debug(x) cerr << #x << ": " << x << endl
#define pb push_back
#define eb emplace_back
#define set0(a) memset(a,0,sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define dwn(i,a,b) for(int i=(a);i>=(b);i--)
#define ceil(a,b) (a+(b-1))/(b)
#define all(x) (x).begin(), (x).end()
#define SUM(a) accumulate(all(a), 0LL)
#define MIN(a) (*min_element(all(a)))
#define MAX(a) (*max_element(all(a)))
#define lb(a, x) distance(begin(a), lower_bound(all(a), (x)))
#define ub(a, x) distance(begin(a), upper_bound(all(a), (x)))
#define INF 0x3f3f3f3f
#define ll_INF 0x7f7f7f7f7f7f7f7f
using pii = pair<int, int>;
using pdd = pair<double, double>;
using vi = vector<int>;
using vvi = vector<vi>;
using vb = vector<bool>;
using vpii = vector<pii>;
using ll = long long;
using ull = unsigned long long;
inline void read(int &x) {
int s=0;x=1;
char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-')x=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
x*=s;
}
const int N=2e5+5;
int n, m, q;
int mp[N];
int w[N];
int last[N], pre[N][25];
int go[N]; // 从当前位置跳 n 次能得到的最大下标。
void get_pre(){
rep(j,1,20) rep(i,1,m) pre[i][j]=pre[pre[i][j-1]][j-1];
}
int get_go(int u){
int cur=n-1;
dwn(i,20,0) if(cur-(1<<i)>=0){
cur-=(1<<i);
u=pre[u][i];
}
return u;
}
int st[N][25], Log[N];
void get_st(){
rep(i,2,N-1) Log[i]=Log[i/2]+1;
rep(j,0,25) for(int i=1; i+(1<<j)-1<=m; i++){
if(!j) st[i][j]=go[i];
else st[i][j]=max(st[i][j-1], st[i+(1<<j-1)][j-1]);
}
}
int query(int l, int r){
int t=Log[r-l+1];
return max(st[l][t], st[r-(1<<t)+1][t]);
}
int main(){
cin>>n>>m>>q;
rep(i,1,n){
int v; read(v);
mp[v]=i;
}
rep(i,1,m) read(w[i]), w[i]=mp[w[i]];
rep(i,1,m){
int v=w[i];
int prev=(v-1? v-1: n);
pre[i][0]=last[prev];
last[v]=i;
}
get_pre();
rep(i,1,m) go[i]=get_go(i);
get_st();
while(q--){
int l, r; read(l), read(r);
if(query(l, r)>=l) cout<<'1';
else cout<<'0';
}
cout<<endl;
return 0;
}
C
凸包。
这题应该是挺套路的,可惜之前没见过 qwq。以后见到什么类似于在曲线上方之类的关键字都可以往将曲线转化为直线然后用凸包处理的方面去想了。
我们做一个映射,将原图上的点 ((X, Y)) 映射到 ((X, Y-X^2)),得到新图。
这样一来,原图上两个点对应的抛物线在新图上就变成直线了。
剩下的任务就是维护一个上凸壳,看看它有多少条边即可(需要特判凸包上直线不存在斜率的情况)。
// Problem: C. U2
// Contest: Codeforces - Codeforces Round #549 (Div. 1)
// URL: https://codeforces.com/contest/1142/problem/C
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#pragma GCC optimize("O3")
#include<bits/stdc++.h>
using namespace std;
#define endl '
'
#define debug(x) cerr << #x << ": " << x << endl
#define pb push_back
#define eb emplace_back
#define set0(a) memset(a,0,sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define dwn(i,a,b) for(int i=(a);i>=(b);i--)
#define ceil(a,b) (a+(b-1))/(b)
#define all(x) (x).begin(), (x).end()
#define SUM(a) accumulate(all(a), 0LL)
#define MIN(a) (*min_element(all(a)))
#define MAX(a) (*max_element(all(a)))
#define lb(a, x) distance(begin(a), lower_bound(all(a), (x)))
#define ub(a, x) distance(begin(a), upper_bound(all(a), (x)))
#define INF 0x3f3f3f3f
#define ll_INF 0x7f7f7f7f7f7f7f7f
using pii = pair<int, int>;
using pdd = pair<double, double>;
using vi = vector<int>;
using vvi = vector<vi>;
using vb = vector<bool>;
using vpii = vector<pii>;
using ll = long long;
using ull = unsigned long long;
#define int ll
inline void read(int &x) {
int s=0;x=1;
char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-')x=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
x*=s;
}
const int N=1e5+5;
int n;
struct Node{
int x, y;
bool operator < (const Node &o)const{
return x==o.x? y<o.y: x<o.x;
}
}q[N];
int stk[N], top;
bool del(Node a, Node b, Node c){
return (c.y-b.y)*(b.x-a.x)>=(c.x-b.x)*(b.y-a.y);
}
void get_convex(){
sort(q+1, q+1+n);
rep(i,1,n){
while(top>=2 && del(q[stk[top-1]], q[stk[top]], q[i])) --top;
stk[++top]=i;
}
}
signed main(){
cin>>n;
rep(i,1,n){
int x, y; read(x), read(y);
y-=x*x;
q[i]={x, y};
}
get_convex();
// rep(i,1,top) cerr<<q[stk[i]].x<<' '<<q[stk[i]].y<<endl;
int res=0;
rep(i,1,top-1) if(q[stk[i]].x!=q[stk[i+1]].x) res++;
cout<<res<<endl;
return 0;
}