1. 线性回归
X，Y是线性的
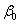是偏置（有点像截距），防止Y为0，矩阵表示时，为全1
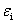：数据集收集的时候有误差（高斯误差，均值为0）
表达向量很相似
D：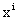
和
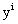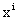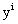，代表所有的数据，和相互独立
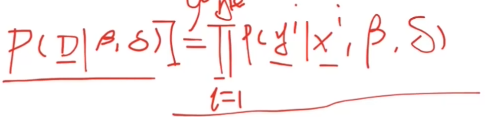
2. Basic Expansion
2.1 使用Basis expansion捕捉自变量和因变量的非线性关系
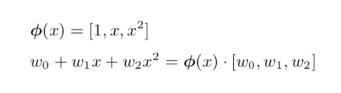
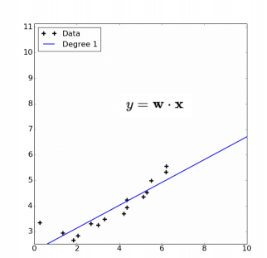
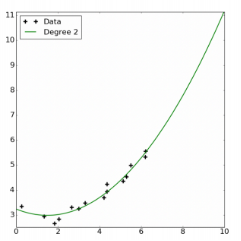
2.2 理解Bias-variance的关系
2.3 过拟合与正则化
过拟合
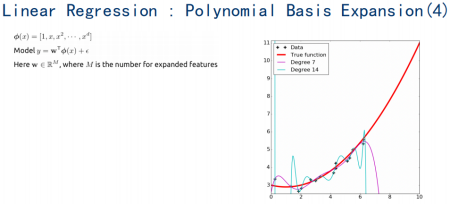
获取更多训练数据防止过拟合
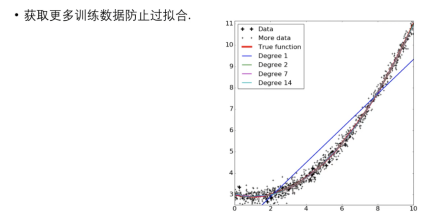
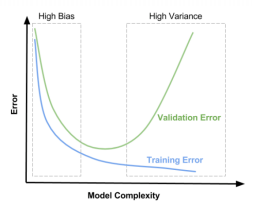
模型与train和valid集的关系
High Varinance：数据对于模型的影响很大
3. 正则化Regularization
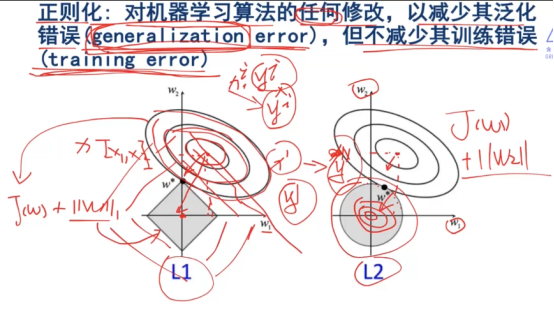
解决一个bias和variance之间的平衡问题。
梯度的反方向朝着圆心，圆心取得最小值
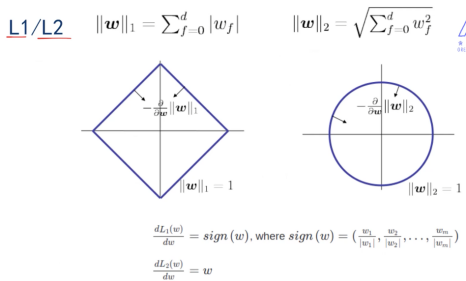
综合损失函数和正则化的函数的等高线拼接在一起，得到最小值
3.1 L1有作特征选择的特性
Lamda 的大小可调整
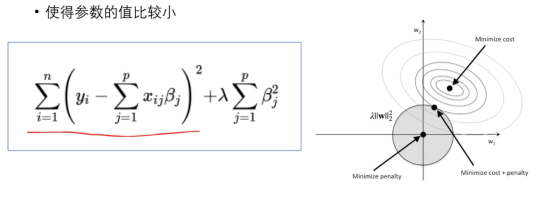
3.2 L2
4. Ridge，Lasso，Bias-Variance，ElasticNet
4.1 Ridge：L1+回归
4.2 Lasso：L2+回归
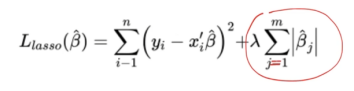
Lasso可以相当于做了一系列的特征工程，但是ridge做不到
允许相关预测变量的存在：是因为当lamda足够大的时候可以忽略x*x^T
实际模型应用中，需要交叉验证进行测试，看看L1好还是L2好，应该选择啥
4.3 ElasticNet： L1+L2
5. 逻辑回归（logistic）
5.1 定义：
逻辑回归=分类！= 回归
希望我们y在[0,1]
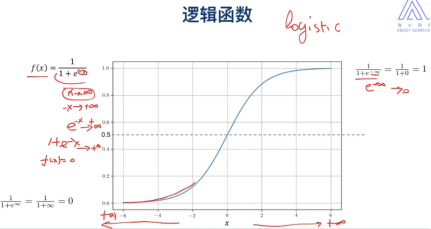
因为sigmod的特殊性，我们可以用线性的方式来表示非线性：
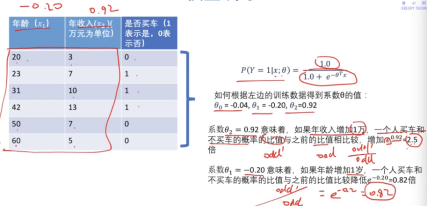
5.2 损失函数
梯度下降法更新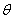
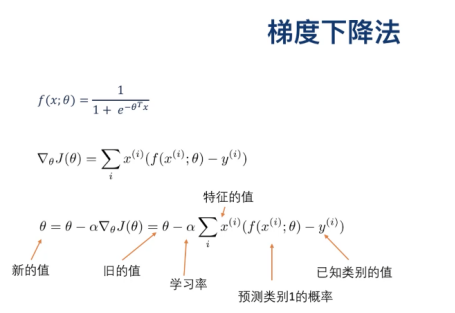
逻辑回归的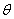
的物理意义：
5.3 似然函数
似然函数和损失函数之间差了个‘负’
6. Softmax 多元逻辑回归
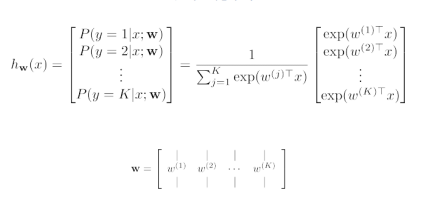
7. 梯度下降算法
7.1 定义
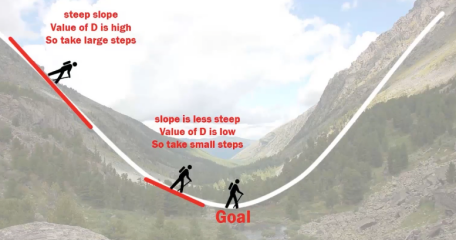
7.2 批梯度下降法
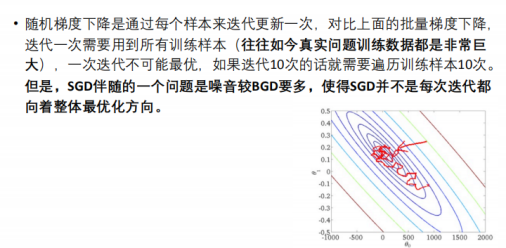
7.3 随机梯度下降法
7.4 小批量的梯度下降法*(用的最多)
