快速排序是对冒泡排序的一种改进,是所有内部排序算法中平均性能最优的排序算法。其基本思想是基于分治法的:在待排序数组L[1...n]中任取一个元素pivot作为基准,从数组的两端开始扫描。设两个指示标志(low指向起始位置,high指向末尾),先从后向前扫描(high递减),如果high位置的元素小于pivot,就交换low和high位置的元素,然后从前向后扫描(low递增),如果low位置的元素大于pivot,就交换low和high位置的元素。重复上述过程,直到low>=high,然后把基准放到low位置上,一趟排序就完成了,将一个元素(基准)放到了最终位置上,不产生有序子序列。将待排序数组划分为两部分即L[1...k-1]和L[k+1...n],使得前半部分L[1...k-1]所有元素小于pivot,后半部分L[k+1...n]所有元素大于或等于pivot。接着采用递归的方式分别对前半部分和后半部分排序,直到每部分只有一个元素或空为止,即所有元素放在了最终位置上。
之所以快速排序比较快,是因为相比于冒泡排序,每次交换是跳跃式的。每次排序时选取一个基准,将小于基准的数全部放到基准点的左边,将大于或等于基准的数全部放到基准的右边,在每次交换时不会像冒泡排序一样只能在相邻的数之间进行交换,增大了交换距离,减少了总的比较和交换次数,加快了速度。在最坏情况下,仍可能交换相邻的两个数。
假设对“6 1 2 7 9 3 4 5 10 8”这10个数进行排序:
从后向前扫描
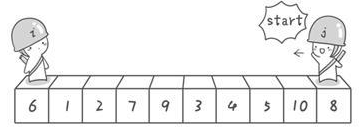
交换7和5
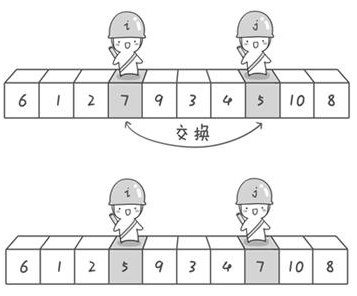
交换之后:6 1 2 5 9 3 4 7 10 8
交换9和4

交换之后:6 1 2 5 4 3 9 7 10 8
i>=j,交换6和3
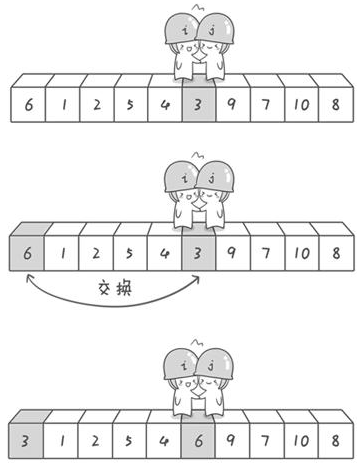
交换之后:3 1 2 5 4 6 9 7 10 8
一趟排序结束。
1 public class QuickSort {
2
3 public static void quickSort(int[] arr, int low, int high) {
4 // 至少有两个元素需要排序
5 if (low < high) {
6 int curLow = low;
7 int curHigh = high;
8 int temp = arr[low];
9
10 while(curLow < curHigh) {
11 // 从右向左扫描,寻找第一个比基准小的数
12 while(curLow < curHigh && arr[curHigh] >= temp) {
13 curHigh--;
14 }
15 arr[curLow] = arr[curHigh];
16
17 // 从左向右扫描,寻找第一个比基准大的数
18 while(curLow < curHigh && arr[curLow] <= temp) {
19 curLow++;
20 }
21 arr[curHigh] = arr[curLow];
22 }
23
24 // 基准归位
25 arr[curLow] = temp;
26
27 // 基准位置左边子序列递归排序
28 quickSort(arr, low, curLow - 1);
29 // 基准位置左边子序列递归排序
30 quickSort(arr, curLow + 1, high);
31 }
32 }
33
34 public static void main(String[] args) {
35 int[] arr = {15, 1, 17, 3, 6, 8};
36 QuickSort.quickSort(arr, 0, arr.length - 1);
37
38 for (int i = 0, length = arr.length; i < length; i++) {
39 System.out.printf(" %d", arr[i]);
40 }
41 }
42
43 }
结果如下:
1 3 6 8 15 17
上述代码每次以当前数组中第一个元素作为基准对数组进行划分。
快速排序性能分析:
空间复杂度:因为快速排序是递归的,所以需要借助一个递归工作栈来保存每一层递归调用的必要信息,容量应与递归调用的最大深度一致。最坏情况下n-1次递归调用,栈的深度为O(n);最好和平均情况下栈的深度为O(log2n)。所以,空间复杂度在最坏情况下为O(n),平均情况下为O(log2n)。
时间复杂度:快速排序的性能主要取决于划分操作的好坏。最坏情况下待排序数组基本有序或基本逆序时,每一次递归划分的两个区域分别包含n-1个元素和0个元素,快速排序退化成冒泡排序,时间复杂度为O(n2)。最好情况下最平衡划分,两个子数组长度不超过n/2,时间复杂度为O(nlog2n)。而快速排序平均情况下运行时间接近于最好情况下的运行时间,即时间复杂度在最坏情况下为O(n2),平均情况下为O(nlog2n)。
稳定性:如果右端区间有两个相同的关键字,且均小于基准,那么交换到左端区间后,它们的相对次序会变化,即快速排序不稳定。例如,表L={3, 2, 2},经过一趟排序后L={2, 2, 3},最终结果是L={2, 2, 3},2与2的相对次序发生了变化。
改进方案
1 使用直接插入排序
当递归过程中划分得到的子数组长度较小时,可以使用直接插入排序完成排序工作。
1 public static void quick(int []array ,int lo,int hi){
2 if(hi-lo+1<10){
3 insertSort(array);
4 }else{
5 quickSort(array,lo,hi);
6 }
7 }
2 选取好的基准
尽量选取可以把元素平衡划分的基准,有三种方法:固定切分,随机切分和三取样切分。固定切分的效率低。随机切分是常用的一种切分,效率高,最坏情况下时间复杂度有可能为O(n2)。三取样切分最理想,具体操作:选取数组的头尾和中间这3个元素,取这3个元素的中间值作为基准。
1 public static int partition(int []array,int lo,int hi){
2 //三数取中
3 int mid=lo+(hi-lo)/2;
4 if(array[mid]>array[hi]){
5 swap(array[mid],array[hi]);
6 }
7 if(array[lo]>array[hi]){
8 swap(array[lo],array[hi]);
9 }
10 if(array[mid]>array[lo]){
11 swap(array[mid],array[lo]);
12 }
13 int key=array[lo];
14
15 while(lo<hi){
16 while(array[hi]>=key&&hi>lo){
17 hi--;
18 }
19 array[lo]=array[hi];
20 while(array[lo]<=key&&hi>lo){
21 lo++;
22 }
23 array[hi]=array[lo];
24 }
25 array[hi]=key;
26 return hi;
27 }
28
29 public static void swap(int a,int b){
30 int temp=a;
31 a=b;
32 b=temp;
33 }
34 public static void sort(int[] array,int lo ,int hi){
35 if(lo>=hi){
36 return ;
37 }
38 int index=partition(array,lo,hi);
39 sort(array,lo,index-1);
40 sort(array,index+1,hi);
41 }
参考资料
《2017年数据结构联考复习指导》 P287-288