蒟蒻林荫小复习——克鲁斯卡尔重构树

这是一个冷门到不能再冷门的东西，至于这东西有什么用，且听我慢慢道来。

现在给定一张无向图，每个点有一个点权，每条边有一个边权。现在给出许多询问三元组（X,Y,Z），要求求出从X出发，只能走边权不超过Y的边，所能走到边权第Z大的点的点权是多少？（BZOJ3551）

如果离线的话，大佬们好像可以用主席树套树之类的鬼东西实现，我诚实的说，我不会！！！

但是要是在线的话，我们就可以引入这个神奇的东西——克鲁斯卡尔重构树了。

克鲁斯卡尔大家都会吧，不会右转幼儿园。

克鲁斯卡尔的原理是对每条边进行排序，然后贪心选取最小的可加入边。因为克鲁斯卡尔所选取的边一定都是可加入的最小的，因此可以保证，上面问题的答案一定是在最小生成树上执行得出的。

重构树就是根据克鲁斯卡尔的原理，对每一条边，并不直接连接到树上，而是新开一个替代点，用来和应当连接的部分相接（也有可能一个图中的原点和一个替代点相连，以此取代原点和替代点所代表的两点的连接）。

那么这个点的点权就是原图中两点间的边权，因为克鲁斯卡尔是从最小的边权开始加入的，那么由此构成的重构树的点权一定是从叶子到根递增的。

虽然很丑，凑合着看吧，蓝笔为点的编号（点权），紫笔为边权。

那么所生成的重构树则如左图（带t的点是新生成的替代点，也就是说，原来的点只存在于叶子节点

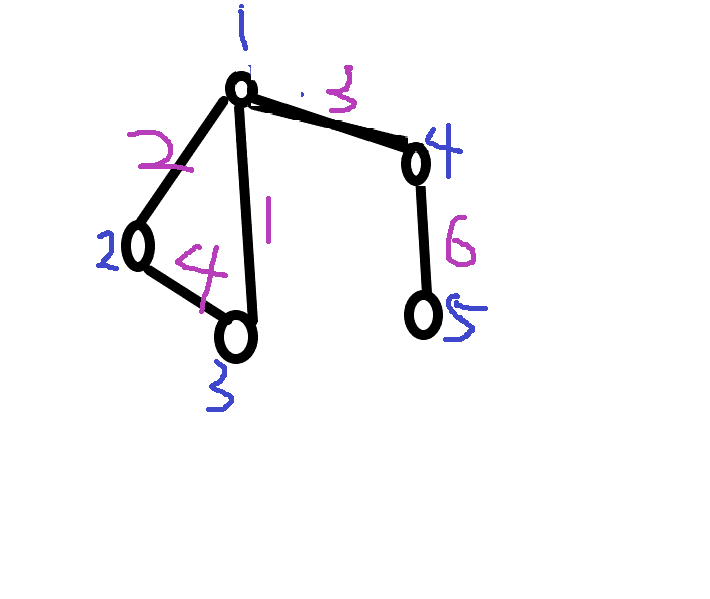
那这样是不是就可以发现：在克鲁斯卡尔重构树中，每一颗子树中任意叶子节点之间的通路中边权最大值不会超过该子树根节点的权值？

因为每次被加入的都是权值更大的边，因此对于替代点而言，点权越小，越处于树的底部。那么是不是对于上面的问题就有点想法了？

我们可以先构造出克鲁斯卡尔重构树，然后每次通过树上倍增找到一个节点U使得Val[U]<=Y且Val[U]尽可能的大，而且我们是否可以发现一个神奇的性质，在原图上每一个节点，都作为克鲁斯卡尔重构树的一个且仅一个叶子节点出现？

那么我们就可以直接用主席树解决这个问题了。

因为我们已经求出了节点U，保证以U为根的子树内所有叶子节点都可以通过最长边权不超过Y的边到达，那么是否可以将以某个节点为根的子树中所有叶子节点的集合视为一个区间呢？

答案是肯定的，下面就剩下一个主席树维护区间最小值了。不会的请百度搜索《蒟蒻林荫小复习——主席树》即可。

直接用主席树维护克鲁斯卡尔重构树的每个叶子节点，然后根据求出的U选择正确的区间，求值即可。

最后放个代码（蒟蒻林荫写了一晚上这个东西）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
int Val[100001],fa[100001],BZ[100001][26],S[100001],a[100001];
vector<int> b[100001];//重构树
int dfn[100001],low[100001],rk[100001];
//dfn代表每个虚构点的子树所包含的第一个实际点，low代表最后一个
//两者即可控制出一个区间 
struct PE
{
    int u,v,val;
};
PE edge[500001];
struct PES
{
    int ls,rs,sums;
};
PES t[1600001];
int rt[100001];
int n,m,q,cnt,tot,limt,top,num;
bool Function(PE x,PE y)
{
    return x.val<y.val; 
}
int Find(int x)
{
    return fa[x]==x?fa[x]:fa[x]=Find(fa[x]);
}
void DFS(int x,int ff)
{
    if(x<=n)
    {
        dfn[x]=++limt;
        low[x]=limt;
        rk[limt]=x;
    }
    else
    {
        dfn[x]=998244353;
        low[x]=0;
    }
    BZ[x][0]=ff;
    for(int i=b[x].size()-1;i>=0;i--)
    {
        DFS(b[x][i],x);
        dfn[x]=min(dfn[x],dfn[b[x][i]]);
        low[x]=max(low[x],low[b[x][i]]);
    }
}
void ADD(int &x,int l,int r,int p)
{
    t[++num]=t[x];++t[x=num].sums;if(l==r)return;
    int mid=(l+r)>>1;
    if(p<=mid)ADD(t[x].ls,l,mid,p);
    else ADD(t[x].rs,mid+1,r,p);
}
/*int Query(int B2,int B1,int l,int r,int K)
{
    if(l==r)
    {
        return S[l];
    }
    int mid=(l+r)>>1;
    int sum=t[t[B2].rs].sums-t[t[B1].rs].sums;
    if(sum>=K)
    {
        return Query(t[B2].rs,t[B1].rs,mid+1,r,K);
    }
    else
        return Query(t[B2].ls,t[B1].ls,l,mid,K-sum);
}*/
int Query(int A,int B,int l,int r,int K)
{
    if(l==r)return S[l];
    int mid=(l+r)>>1,sum=t[t[A].rs].sums-t[t[B].rs].sums;
    if(sum>=K)return Query(t[A].rs,t[B].rs,mid+1,r,K);
    else return Query(t[A].ls,t[B].ls,l,mid,K-sum);
}
int BZENG()
{
    for(int i=1;i<=19;i++)
    {
        for(int j=1;j<=tot;j++)
        {
            BZ[j][i]=BZ[BZ[j][i-1]][i-1];
        }
    }
}
int main()
{
    freopen("txt.in","r",stdin);
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&S[i]);
        a[i]=S[i];
    }
    sort(S+1,S+1+n);
    top=unique(S+1,S+1+n)-S-1;
    for(int i=1;i<=n;i++)
    {
        a[i]=lower_bound(S+1,S+1+top,a[i])-S;
    }
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&edge[i].u,&edge[i].v,&edge[i].val);
    }
    sort(edge+1,edge+1+m,Function);
    for(int i=1;i<=n;i++)
    {
        fa[i]=i;
    }
    tot=n;
    for(int i=1;i<=m;i++)
    {
        int u=Find(edge[i].u);
        int v=Find(edge[i].v);
        if(u==v)
        {
            continue;
        }
        ++tot;
        fa[tot]=fa[u]=fa[v]=tot;
        Val[tot]=edge[i].val;
        b[tot].push_back(u);
        b[tot].push_back(v);
    }
    DFS(tot,0);
    BZENG();
    for(int i=1;i<=n;i++)
    {
        ADD(rt[i]=rt[i-1],1,top,a[rk[i]]);
    }
    int lans=0,a1,a2,a3;
    while(q--)
    {
        int v,x,K;
        scanf("%d%d%d",&v,&x,&K);
        if(lans!=-1)v^=lans,x^=lans,K^=lans;
        for(int i=19;~i;--i)
            if(BZ[v][i]&&Val[BZ[v][i]]<=x)
                v=BZ[v][i];
        if(low[v]-dfn[v]+1<K)lans=-1;
        else lans=Query(rt[low[v]],rt[dfn[v]-1],1,top,K);
        printf("%d
",lans);
    }
    return 0;
}

完结撒花！！！