part0 什么是多项式?
[f(x) = sumlimits_{i = 0}^{n - 1} a_i * x^i
]
点值表示
((x_0,f(x_0)),(x_1,f(x_1))...(x_{n-1}, f(x_{n-1})))
part1 离散傅里叶变换
复数
首先我们要了解复数 即 $i = sqrt {-1} $
一个数有实部和虚部 即 (a = x + y * i ~~ (x, y))
原来的实数运算相当于在一个一维数轴上进行移动,复数则是在二维平面上运动
复数运算
一句话来说就是 摸长相乘,幅角相加
c++中提供了复数模板
#include <complex>
complex <double> a;
可以像正常数一样加减乘除
单位根
下面默认 (n) 是2的整数次幂, 不够在末尾补0
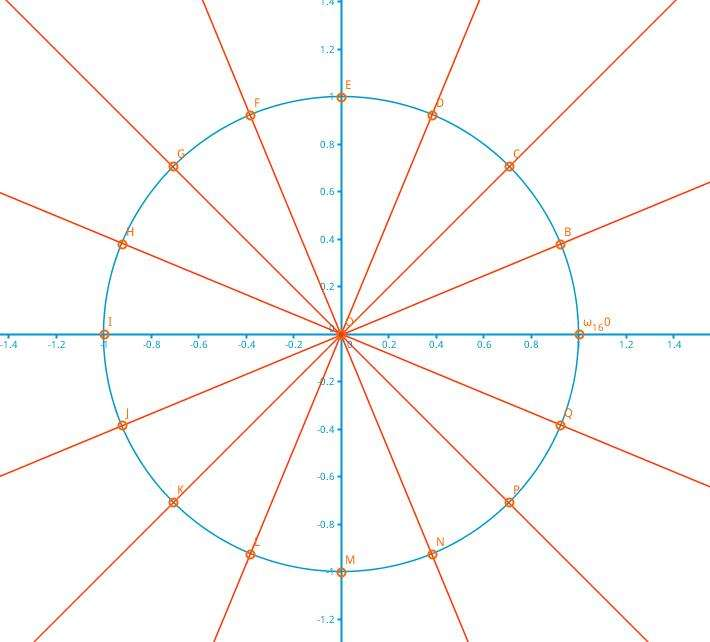
对于一个 (n) 次多项式我们把一个单位圆分成 (n) 份
[omega_n^0, omega_n^1, omega_n^2,...,omega_n^{n - 1}
]
[omega_n^k = (cos(frac k n * 2 * pi), sin(frac k n * 2 * pi))
]
(omega_n^k) 叫做单位根 , (omega_n^1) 就叫做 (n) 次单位根 , 根据复数运算 (omega_n^k = (omega_n^1)^k)
单位根性质
[�egin{cases} omega_{2n}^{2k} = omega_n^k \omega_n^{k + frac 2 n} = - omega_n ^ k end{cases}
]
都比较显然把。。。
把 (omega_0, omega_1, omega_2,...,omega_{n - 1}) 带入多项式,得到 (f(omega_0), f(omega_1), f(omega_2),...,f(omega_{n - 1})),({(omega_i, f(omega_i))}) 这种点值表示就是离散傅里叶变换
离散傅里叶变换的逆变换
设 (y_0, y_1, ... , y_{n -1} = f(omega_n^0), f(omega_n^1), ... , f(omega_n^{n - 1}))
设函数
[F(x) = sumlimits_{i = n}^{n - 1} y_i * x^i
]
将单位根的倒数 (omega_n^{-0}, omega_n^{-1},...omega_n^{-(n - 1)}) 带入 (F(x))
得到
[z_k= F(omega_n^{-k})= sum_{i = 0} ^ {n - 1} y_i * omega_n^{-k}
]
[= sum_{i = 0} ^ {n - 1} sum_{j = 0} ^ {n - 1} a^j * (omega_n^i) ^ j * (omega_n^{-k}) ^ i
]
[=sum_{j = 0} ^ {n - 1} a^j sum_{i = 0} ^ {n - 1} (omega_n^j) ^ i * (omega_n^{-k})^i
]
[=sum_{j = 0} ^ {n - 1} a^j sum_{i = 0} ^ {n - 1} (omega_n^{j - k})^i
]
根据等比数列求和公式
[z_k = a_k * n
]
[a_k = frac {z_k} n
]
这样,我们用点值表示推出了系数
快速傅里叶变换
已知
[f(x) = sum a_i * x^i
]
把 (f(x)) 分成奇偶两部分
[f(x) = (a_0x^0 + a_2x^2 + a_4x ^ 4 + ...) + (a_1 x ^ 1 + a_3 x ^3 + a_5 x ^ 5 + ...)
]
设
[�egin{cases} A(x) = a_0x^0 + a_2 x ^ 1 + a_4 x ^2... \ B(x) = a_1 x ^ 0 + a_3x^1 + a_5x^2...end{cases}
]
[f(x) = A(x^2) + x * B(x ^ 2)
]
把 (omega_n^k (k < frac n 2)) 带入
[f(omega_n^k) = A(omega_n^{2k}) + omega_n^k B(omega_n^{2k})
]
[= A(omega_{frac n 2}^k) + omega_n^k B(omega_{frac n 2} ^ k)
]
把 (omega_n^{k + frac n 2} ( k < frac n 2)) 带入
[f(omega_n^{k + frac n 2}) = A(omega_n^{2k} * omega_n^n) -omega_n^k B(omega_n^{2k} * omega_n^n)
]
[= A(omega_{frac n 2}^{k}) - omega_n^k B (w_{frac n 2}^k)
]
n = 1时直接返回就行了
