快速排序学习笔记

快速排序

---

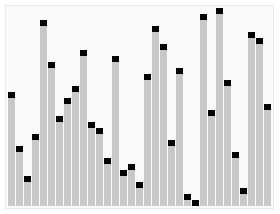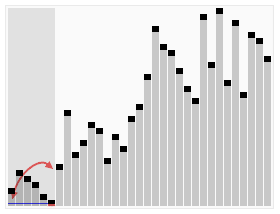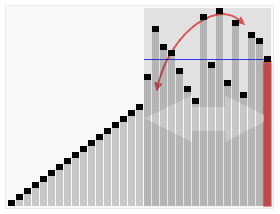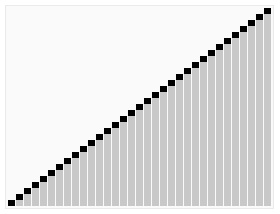
排序过程

基本思想

快速排序和冒泡排序一样，是一种基于比较和交换的排序算法，快速排序基于分治法思想，对冒泡排序进行了优化。

其基本思想为：从序列中挑选一个基准元素，将序列划分成两个部分，其中一部分的元素比另一部分的元素小，然后对这两部分分别重复上述过程，整个排序过程可以递归进行。

      

---

 

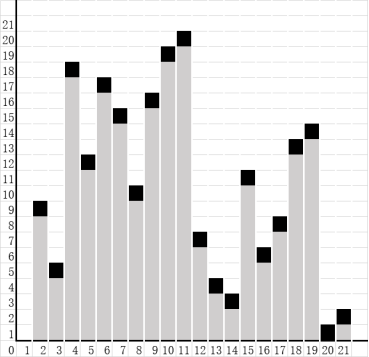
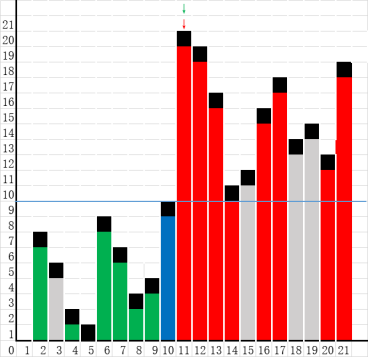
（1）从序列挑选一个元素作为基准元素（基准元素的挑选将影响排序效率）；

（2）使用基准元素将序列划分成两个子序列，其中一个子序列的所有元素都小于另一个序列；

（3）对子序列重复上述过程，直到子序列中只有一个元素。

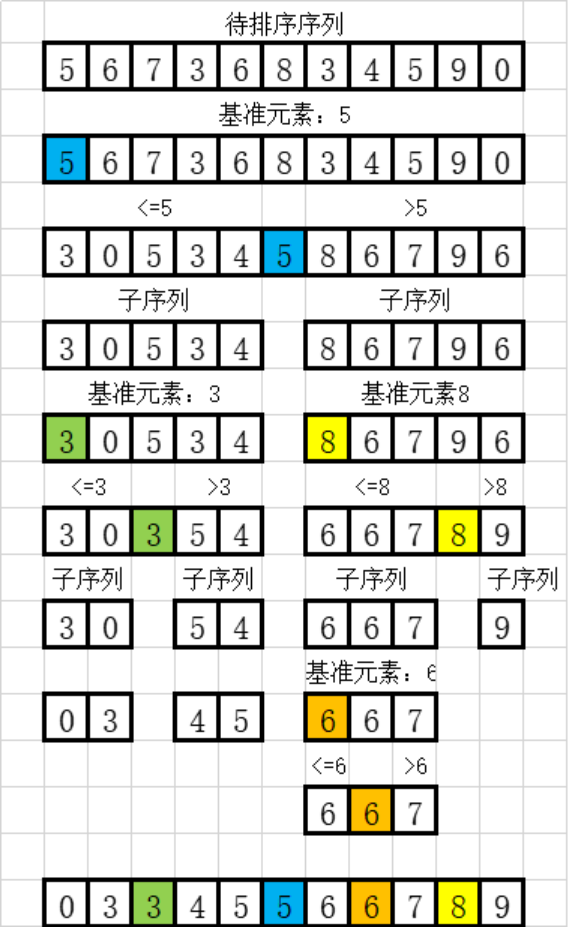
上图排序过程中使用以序列第一个元素作为基准元素

分析

 1、什么时候使用快速排序比较合适？快速排序为什么快速？

    数据规模越大，快速排序性能越优。快速排序的优越性体现在，没有多余的比较，总体的比较次数较少。

2、最好情况，最坏情况？（以升序为例）

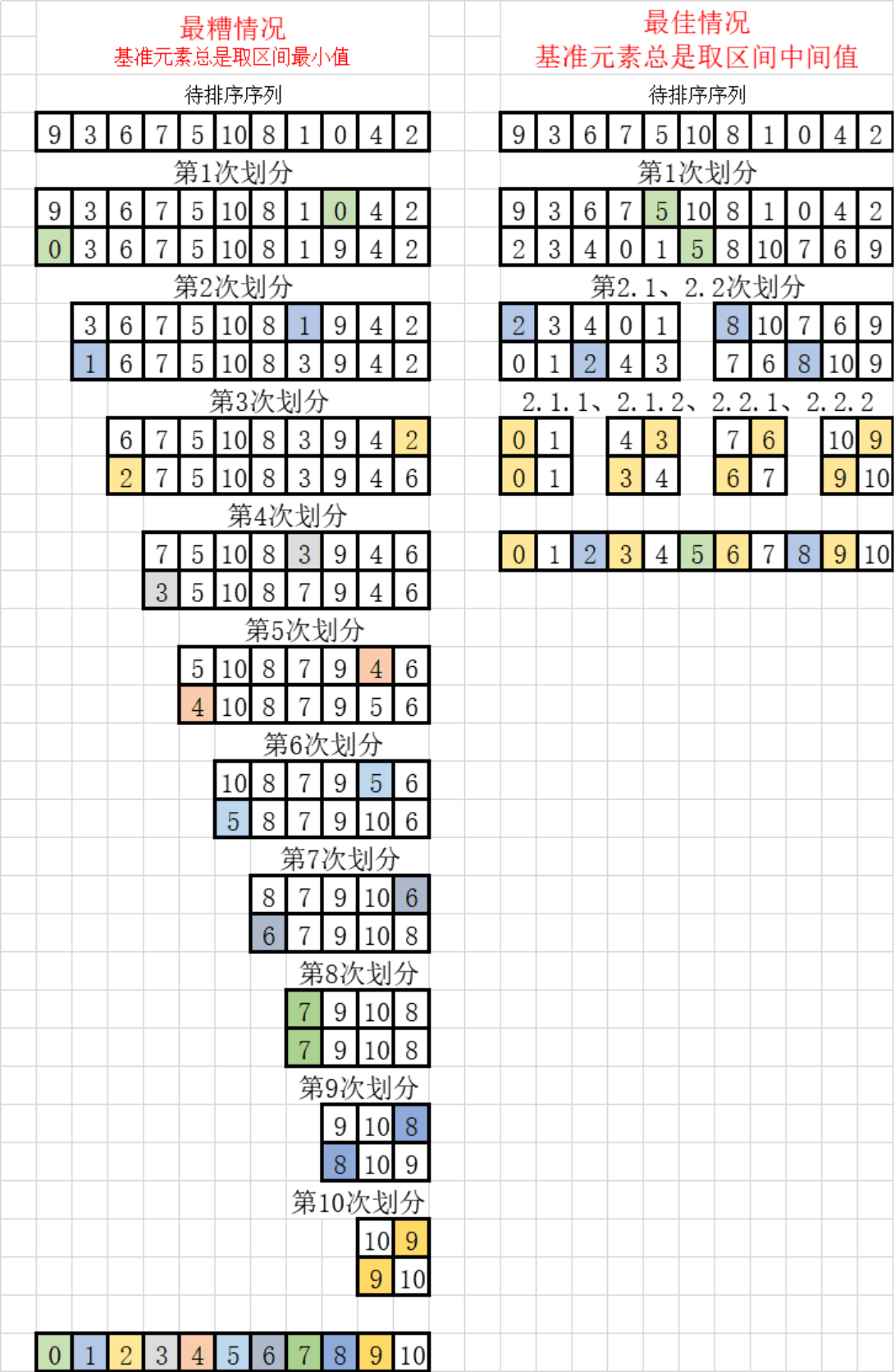
 上文曾经提到，基准元素的选择将影响排序的效率，最坏情况，每次选取的基准元素都是区间最小元素，最佳情况，每次选取的基准元素都是区间中间值。

最坏情况：

    最坏情况下，总共进行n-1次划分。

    第i次划分时，区间长度为n-i+1（等差数列，通项公式A_i = A₁+(n-1)d），进行n-i次比较。

总共进行n(n-1)/2次比较（等差数列求和），时间复杂度O(n²)。

最佳情况：

    最好情况下，共进行n次划分。

    时间复杂度O(nlogⁿ)。

平均时间复杂度：O(nlog₂ⁿ)

代码：

    /**
     * 划分区间
     *
     * @param randomArray - 待排序序列
     * @param low         - 排序区间下界
     * @param high        - 排序区间上界
     * @return - 划分结束后，基准元素所在的位置
     */
    public static int divide(Integer[] randomArray, int low, int high) {
        //如果区间只有两个元素
        if (high - low == 1) {
            int temp;
            if (randomArray[low] > randomArray[high]) {
                temp = randomArray[low];
                randomArray[low] = randomArray[high];
                randomArray[high] = temp;
            }
            return -1;
        }
        //1、选择基准元素
        int datum = low;
        //2、遍历区间，划分区间。
        int temp;
        while (low < high) {
            //
            while (low < high && randomArray[low] <= randomArray[datum]) {
                low++;
            }
            //
            while (high > low && randomArray[high] > randomArray[datum]) {
                high--;
            }
            temp = randomArray[low];
            randomArray[low] = randomArray[high];
            randomArray[high] = temp;
        }
        //交换基准元素至正确位置
        temp = randomArray[datum];
        randomArray[datum] = randomArray[low - 1];
        randomArray[low - 1] = temp;
        return low - 1;
    }

    /**
     * 快速排序
     *
     * @param randomArray - 待排序序列
     * @param low         - 排序区间下界
     * @param high        - 排序区间上界
     * @return - 有序序列
     */
    public static Integer[] quickSorted(Integer[] randomArray, int low, int high) {
        //区间元素大于1才有排序必要
        if (high - low >= 1) {
            //1、划分区间
            int datum = divide(randomArray, low, high);
            //2、是否可以继续划分
            if (datum != -1) {
                quickSorted(randomArray, low, datum - 1);
                quickSorted(randomArray, datum + 1, high);
            }
        }
        return randomArray;
    }