UVA_Digit Puzzle UVA 12107

If you hide some digits in an integer equation, you create a digit puzzle. The figure below shows two valid
digit puzzles. Hidden digits are represented by squares, and other digits are shown. The numbers involved in
this problem are all positive integers, written in decimal forms without leading zeros.

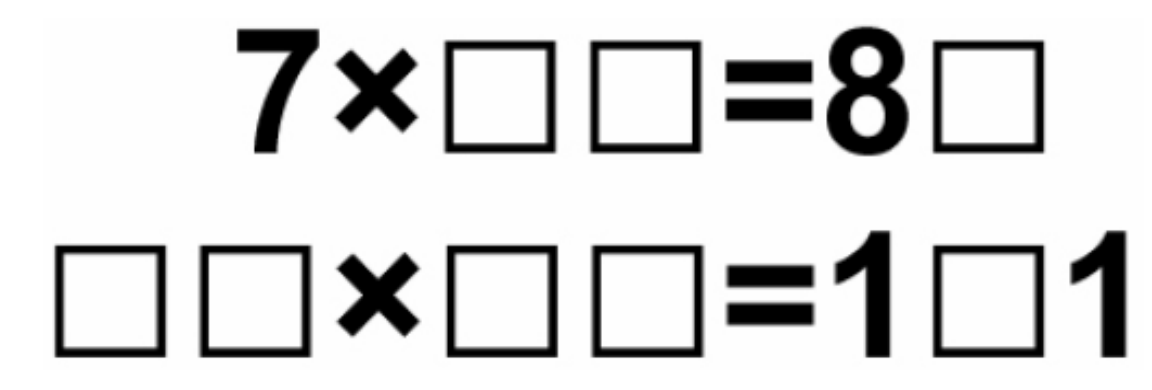
Fig 1. two good digit puzzles
If a digit puzzle has a unique solution, we call it a good puzzle. Both puzzles shown above are good puzzles.
The solution to the first puzzle is 7 * 12 = 84 , while the solution to the second one is 11 * 11 = 121 .
You are already given some digit puzzles, but some of them are not good. Your task is to convert these
puzzles into good ones. You can change any wildcard character (i.e. hidden digits) into a real digit, any real
digit to a wildcard character, or a real digit to another real digit, but you cannot insert or remove any character
at any place. The number of changed characters should be minimized.
In this problem, the puzzle is always in the form `` a×b = c ", and `` a×b " and `` b×a " should be considered
different if a is not equal to b . It is allowed that all digits of both a and b are shown (e.g 12×34 = * * * * ),
though that puzzle is actually a simple multiplication problem. Write a program to make good puzzles.
Input
The input contains several test cases. Each test case contains three non-empty strings, x , y , z , having at most
2, 2 and 4 characters respectively. Each character is a digit or a wildcard `*', x will not begin with a zero
character. The last test case is followed by a single zero, which should not be processed.
Output
For each test case, print the case number and the converted puzzle. If more than one optimal solution is found,
the lexicographically first one should be printed (remember that ``*" is before ``0"). There is always a
solution.
3784 - Digit Puzzle 1/2
Sample Input
7 ** 8*
** ** ***
0
Sample Output
Case 1: 7 ** 8*
Case 2: ** ** 1*1

解题报告

采用迭代加深搜索，一个dfs用于构造，一个dfs用于检查解的合理性。

注意检查的dfs如果发现有两组及以上解可行就直接返回（不唯一，肯定不合法）

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;
char s[3][6],len[3];
int caculate[6] = {0,1,10,100,1000,10000},maxd;
char change[11] = {'*','0','1','2','3','4','5','6','7','8','9'};
int lk = 0;

int check_result()
{
char check_str[10];
char sss[10];
int  t0 = 0,t1 = 0,t2,cot = 0;
for(int i = 0 ; i < len[0]; ++ i)
 t0 = t0*10 + s[0][i] - '0';
for(int i = 0 ; i < len[1]; ++ i)
 t1 = t1*10 + s[1][i] - '0';
t2 = t0*t1;
for(int i = 0 ; i <len[2];++i)
 {
     check_str[len[2] - i - 1] = t2 % 10 +  '0';
     t2 /= 10;
 }
if (t2 != 0 || check_str[0] == '0') /*Not Equal Length with Len[2]*/
 return 0;
for(int i = 0;i<len[2];++i)
 if(check_str[i] != s[2][i] && s[2][i] != '*')
  return 0;
return 1;
}


int check_(int a,int b)
{
  int flag = 0;
  if (a == 2)
   {
        flag = check_result();
        return flag;
   }    
  int ta,tb;
  char ch = s[a][b];
  if (b == len[a] - 1)
   {
       ta = a +1;
       tb = 0;
   }
  else
   {
       ta = a;
       tb = b+1;
   }
 if (s[a][b] == '*')
  {
   for(int i = 1 ; i <= 10 ; ++i)
    if (b == 0 && i == 1) continue;
    else
    {
      s[a][b] = change[i];
      flag += check_(ta,tb);
      if (flag > 1) /* Not Found Solution       */
            break;
    }
   }
  else
    {
      flag += check_(ta,tb);     
    }
s[a][b] = ch; /*Recover The Spot*/
return flag;
}



int dfs(int a,int b,int d)
{
 int flag;
 if (d == maxd)
  {
     flag = check_(0,0);
     if (flag == 1)
      return 1;
     else 
      return 0;    
  }
 if (a == 3)
  return 0;
 int ta,tb;
 char ori = s[a][b];
 if (b == len[a] -1)
  {
      ta = a + 1;
      tb = 0;
  } 
 else
  {
      ta = a;
      tb = b + 1;
  }
 for(int i = 0 ; i <= 10 ; ++ i)
  {
      if (b == 0 && i == 1) continue;
      if (ori == change[i]) 
        {
            s[a][b] = ori;
           flag = dfs(ta,tb,d);
       }
                 
      else
     {
         s[a][b] = change[i];
         flag = dfs(ta,tb,d+1);
     }
     if (flag)
      break;
  }
if (!flag)
 s[a][b] = ori; /*Not Found Sloution,Recover Spot         */
return flag;
}



int main(int argc, char * argv[])
{
 int cas = 0;
 memset(s,0,sizeof(s));
 while(scanf("%s%s%s",s[0],s[1],s[2]) == 3)
  {
      for(int i = 0; i < 3 ;++ i)
           len[i] = strlen(s[i]);
           /*Because input is always has a solution,so there is no limit to deep_Max          */
      printf("Case %d: ",++cas);
    for(int i = 0 ;  ; ++ i)
     {
         maxd = i; /*iterative deepening */          
         if (dfs(0,0,0))
          {
              printf("%s %s %s
",s[0],s[1],s[2]);
              break;
          }
     }
    memset(s,0,sizeof(s));
  }
 return 0;    
}