Position:http://codeforces.com/contest/723
我的情况

啊哈哈,这次raiting肯定要涨,接受过上次的教训,先用小号送肉,大号都是一发切,重回蓝咯
结果。。。

FST!!
不,这次是skip,A题gi了(从小号蒯来没改),其它就都会skip。。。。。。

大号被小号skip,大号还300多名(没WA),做不得卵声。结果小号rank408,+133raiting
恭喜LCFrank10,+279raiting
为了表示我被skip的愤怒,我决定用大号打Vitural

诶,有个人比我吊e,oo
反思
aaa下次用小号一定要改代码
C题没看懂导致A的时间很晚,少了400多分。EF没有时间,要提高时间,与代码的正确性。

全蓝了哦,算了,下次加油吧!頑張って!
官方题解
A. The New Year: Meeting Friends
There are three friend living on the straight line Ox in Lineland. The first friend lives at the point x1, the second friend lives at the point x2, and the third friend lives at the point x3. They plan to celebrate the New Year together, so they need to meet at one point. What is the minimum total distance they have to travel in order to meet at some point and celebrate the New Year?
It's guaranteed that the optimal answer is always integer.The first line of the input contains three distinct integers x1, x2 and x3(1 ≤ x1, x2, x3 ≤ 100) — the coordinates of the houses of the first, the second and the third friends respectively.
7 1 4
6
30 20 10
20
In the first sample, friends should meet at the point 4. Thus, the first friend has to travel the distance of 3 (from the point 7 to the point 4), the second friend also has to travel the distance of 3 (from the point 1 to the point 4), while the third friend should not go anywhere because he lives at the point 4.
Understanding
一个数轴上有三个人,他们要到一个地方聚会,使得每个人到这个地方的距离之和最小。
Solution
Greedy+Sort.我其实还没来得急看题,看了发样例,好像是最大数减最小数,赶快ma完交小号。。当时为了图快,随便搞,其实之后看了题还是可以证明的,如下:
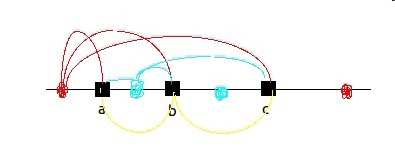
R红色的为一种情况光是c→R,就>c-a(右边的算到a的距离)
B蓝色的一种情况,a→B+c→B=c-a,所以就只与B到b的距离有关
Y黄色,由B推来,当Y=b即为一个点答案为c-a,证毕
Code
// <A.cpp> - Mon Oct 3 19:17:39 2016
// This file is made by YJinpeng,created by XuYike's black technology automatically.
// Copyright (C) 2016 ChangJun High School, Inc.
// I don't know what this program is.
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#pragma GCC push_options
#pragma GCC optimize ("O2")
#define MOD 1000000007
#define INF 1e9
#define IN inline
#define RG register
using namespace std;
typedef long long LL;
typedef long double LB;
const int MAXN=100010;
const int MAXM=100010;
inline int max(int &x,int &y) {return x>y?x:y;}
inline int min(int &x,int &y) {return x<y?x:y;}
inline LL gi() {
register LL w=0,q=0;register char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')q=1,ch=getchar();
while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar();
return q?-w:w;
}
int main()
{
freopen("A.in","r",stdin);
freopen("A.out","w",stdout);
int a=gi(),b=gi(),c=gi();
printf("%d",max(max(abs(a-b),abs(b-c)),abs(a-c)));
return 0;
}
B. Text Document Analysis
Modern text editors usually show some information regarding the document being edited. For example, the number of words, the number of pages, or the number of characters.
In this problem you should implement the similar functionality.
You are given a string which only consists of:
- uppercase and lowercase English letters,
- underscore symbols (they are used as separators),
- parentheses (both opening and closing).
It is guaranteed that each opening parenthesis has a succeeding closing parenthesis. Similarly, each closing parentheses has a preceding opening parentheses matching it. For each pair of matching parentheses there are no other parenthesis between them. In other words, each parenthesis in the string belongs to a matching "opening-closing" pair, and such pairs can't be nested.
For example, the following string is valid: "_Hello_Vasya(and_Petya)__bye_(and_OK)".
Word is a maximal sequence of consecutive letters, i.e. such sequence that the first character to the left and the first character to the right of it is an underscore, a parenthesis, or it just does not exist. For example, the string above consists of seven words: "Hello", "Vasya", "and", "Petya", "bye", "and" and "OK". Write a program that finds:
- the length of the longest word outside the parentheses (print 0, if there is no word outside the parentheses),
- the number of words inside the parentheses (print 0, if there is no word inside the parentheses).
Print two space-separated integers:
- the length of the longest word outside the parentheses (print 0, if there is no word outside the parentheses),
- the number of words inside the parentheses (print 0, if there is no word inside the parentheses).
37
_Hello_Vasya(and_Petya)__bye_(and_OK)
5 4
37
_a_(_b___c)__de_f(g_)__h__i(j_k_l)m__
2 6
Understanding
给你一串字符,每个单词用_or()分开,问在括号外面的最长单词长度与括号里面单词个数。
Solution
细节题,Implementation
Code
// <B.cpp> - Mon Oct 3 19:17:39 2016
// This file is made by YJinpeng,created by XuYike's black technology automatically.
// Copyright (C) 2016 ChangJun High School, Inc.
// I don't know what this program is.
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <cmath>
using namespace std;
const int MAXN=100010;
const int MAXM=100010;
inline int gi() {
register int w=0,q=0;register char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')q=1,ch=getchar();
while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar();
return q?-w:w;
}
char s[MAXN];
int main()
{
freopen("B.in","r",stdin);
freopen("B.out","w",stdout);
int n=gi(),ans=0,x=0;scanf("%s",s);
for(int i=0;i<n;i++){
int j=i;
while(s[j]!='('&&s[j]!='_'&&j<n)j++;
if(j!=i)ans=max(j-i,ans);
if(s[j]=='('){
for(j++;j<n;j++){
if(s[j]==')')break;
int o=j;
while(s[o]!='_'&&s[o]!=')'&&o<n)o++;
if(o!=j)x++,j=o;
if(s[o]==')')break;
}
}
i=j;
}
printf("%d %d",ans,x);
return 0;
}
C. Polycarp at the Radio
Polycarp is a music editor at the radio station. He received a playlist for tomorrow, that can be represented as a sequence a1, a2, ..., an, where ai is a band, which performs the i-th song. Polycarp likes bands with the numbers from 1 to m, but he doesn't really like others.
We define as bj the number of songs the group j is going to perform tomorrow. Polycarp wants to change the playlist in such a way that the minimum among the numbersb1, b2, ..., bm will be as large as possible.
Find this maximum possible value of the minimum among the bj (1 ≤ j ≤ m), and the minimum number of changes in the playlist Polycarp needs to make to achieve it. One change in the playlist is a replacement of the performer of the i-th song with any other group.
The first line of the input contains two integers n and m (1 ≤ m ≤ n ≤ 2000).
The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109), where ai is the performer of the i-th song.
In the first line print two integers: the maximum possible value of the minimum among the bj(1 ≤ j ≤ m), where bj is the number of songs in the changed playlist performed by the j-th band, and the minimum number of changes in the playlist Polycarp needs to make.
In the second line print the changed playlist.
If there are multiple answers, print any of them.
4 2
1 2 3 2
2 1
1 2 1 2
7 3
1 3 2 2 2 2 1
2 1
1 3 3 2 2 2 1
Understanding
给你一列数,要你将其修改。使得1~m的数目最小的最大,且修改数目最小。
My Solution
Greedy.首先要使1~m每个数出现次数最小的最多,平均分配一下,答案为n/m.然后要修改→将出现个数比n/m小的改为>=n/m.Code
// <C.cpp> - Mon Oct 3 19:17:39 2016
// This file is made by YJinpeng,created by XuYike's black technology automatically.
// Copyright (C) 2016 ChangJun High School, Inc.
// I don't know what this program is.
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <queue>
using namespace std;
typedef long long LL;
const int MAXN=2010;
inline LL gi() {
register LL w=0,q=0;register char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')q=1,ch=getchar();
while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar();
return q?-w:w;
}
int a[MAXN],f[MAXN],ans;
int main()
{
freopen("C.in","r",stdin);
freopen("C.out","w",stdout);
int n=gi(),m=gi(),x=n/m;
for(int i=1;i<=n;i++){a[i]=gi();if(a[i]<=m)f[a[i]]++;}
printf("%d ",x);
for(int i=1,j;i<=n;i++)
if(a[i]>m)
for(j=1;j<=m;j++)
if(f[j]<x){
ans++;a[i]=j;f[j]++;break;
}
for(int i=1;i<=m;i++)
if(f[i]<x)
for(int j=1;j<=n;j++){
if(f[i]==x)break;
if(f[a[j]]>x){
f[a[j]]--;f[i]++;ans++;a[j]=i;
}
}
printf("%d
",ans);
for(int i=1;i<=n;i++)printf("%d ",a[i]);
return 0;
}
Zyt's Solution
Greedy.一次性处理,将>m的数丢到栈中。然后处理每一个1~m的数,优先放>m的数。Code
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define inf 2147483640
#define Pi acos(-1.0)
#define free(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
using namespace std;
const int maxn=2010;
int a[maxn],b[maxn],n,m;
int main() {
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++) scanf("%d",&a[i]);
int t=0;
for (int i=1;i<=n;i++) {
if (a[i]>m) t++;
else b[a[i]]++;
}
int ans=n/m,cnt=0;
for (int i=1;i<=m;i++) if (b[i]<ans) {
if (t) {
for (int j=1;j<=n;j++) {
if (a[j]>m) a[j]=i,t--,b[i]++,cnt++;
if (b[i]==ans) break;
}
if (b[i]==ans) continue;
}
for (int j=1;j<=n;j++) {
if (b[a[j]]>ans) {b[a[j]]--;a[j]=i;b[i]++;cnt++;}
if (b[i]==ans) break;
}
}
printf("%d %d
",ans,cnt);
for (int i=1;i<=n;i++) printf("%d ",a[i]);
return 0;
}
D. Lakes in Berland
The map of Berland is a rectangle of the size n × m, which consists of cells of size 1 × 1. Each cell is either land or water. The map is surrounded by the ocean.
Lakes are the maximal regions of water cells, connected by sides, which are not connected with the ocean. Formally, lake is a set of water cells, such that it's possible to get from any cell of the set to any other without leaving the set and moving only to cells adjacent by the side, none of them is located on the border of the rectangle, and it's impossible to add one more water cell to the set such that it will be connected with any other cell.
You task is to fill up with the earth the minimum number of water cells so that there will be exactly k lakes in Berland. Note that the initial number of lakes on the map is not less than k.
The first line of the input contains three integers n, m and k (1 ≤ n, m ≤ 50, 0 ≤ k ≤ 50) — the sizes of the map and the number of lakes which should be left on the map.
The next n lines contain m characters each — the description of the map. Each of the characters is either '.' (it means that the corresponding cell is water) or '*' (it means that the corresponding cell is land).
It is guaranteed that the map contain at least k lakes.
In the first line print the minimum number of cells which should be transformed from water to land.
In the next n lines print m symbols — the map after the changes. The format must strictly follow the format of the map in the input data (there is no need to print the size of the map). If there are several answers, print any of them.
It is guaranteed that the answer exists on the given data.
5 4 1
****
*..*
****
**.*
..**
1
****
*..*
****
****
..**
3 3 0
***
*.*
***
1
***
***
***
Understanding
给你一个字符矩阵,'*'stand for sand,'.'stand for water
一个湖的定义为与边界没有交。求湖的个数<=k的最小填的个数,并且输出方案
Solution
广搜+贪心+sort.先处理边界海.然后将每个湖给抠出来,并记录大小,按大小排序,一个个湖删,因为发现填湖要全部填满,并且边界海也没用,贪心即可。
Code
// <D.cpp> - Mon Oct 3 19:17:39 2016 // This file is made by YJinpeng,created by XuYike's black technology automatically. // Copyright (C) 2016 ChangJun High School, Inc. // I don't know what this program is. #include <iostream> #include <vector> #include <algorithm> #include <cstring> #include <cstdio> #include <queue> #include <cstdlib> #include <cmath> using namespace std; typedef long long LL; const int MAXN=51; inline LL gi() { register LL w=0,q=0;register char ch=getchar(); while((ch<'0'||ch>'9')&&ch!='-')ch=getchar(); if(ch=='-')q=1,ch=getchar(); while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar(); return q?-w:w; } bool f[MAXN][MAXN],u[MAXN][MAXN]; int _x[5]={0,0,-1,1},_y[5]={-1,1,0,0}; struct node{int x, y;}; struct bb{ int s; vector<node>a; bool operator <(bb b)const{return s<b.s;} }p[MAXN*MAXN]; queue<node>q;int n,m; void work(int i,int j){ q.push((node){i,j});u[i][j]=true; while(!q.empty()){ int x=q.front().x,y=q.front().y;q.pop(); for(int o=0,a,b;a=x+_x[o],b=y+_y[o],o<4;o++) if(!f[a][b]&&!u[a][b]&&a>=1&&a<=n&&b>=1&&b<=m) u[a][b]=1,q.push((node){a,b}); } } int main() { freopen("D.in","r",stdin); freopen("D.out","w",stdout); n=gi(),m=gi();int k=gi(),tot=0; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ char ch=getchar(); while(ch!='.'&&ch!='*')ch=getchar(); f[i][j]=bool(ch=='*'); } } for(int i=1;i<=m;i++){ if(!f[1][i]&&!u[1][i])work(1,i); if(!f[n][i]&&!u[n][i])work(n,i); } for(int i=1;i<=n;i++){ if(!f[i][1]&&!u[i][1])work(i,1); if(!f[i][m]&&!u[i][m])work(i,m); } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(!f[i][j]&&!u[i][j]){ q.push((node){i,j});p[++tot].s=1;u[i][j]=true; while(!q.empty()){ int x=q.front().x,y=q.front().y;p[tot].a.push_back((node){x,y});q.pop(); for(int o=0,a,b;a=x+_x[o],b=y+_y[o],o<4;o++) if(!f[a][b]&&!u[a][b]&&a>=1&&a<=n&&b>=1&&b<=m){ u[a][b]=1;q.push((node){a,b});p[tot].s++; } } } sort(p+1,p+1+tot);int ans=0; k=tot-k; for(int i=1;i<=k;i++){ for(int to=p[i].a.size(),j=0,x,y;x=p[i].a[j].x,y=p[i].a[j].y,j<to;j++) f[x][y]=1; ans+=p[i].s; } printf("%d ",ans); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++)putchar(f[i][j]?'*':'.'); cout<<endl; } return 0; }
E. One-Way Reform
There are n cities and m two-way roads in Berland, each road connects two cities. It is known that there is no more than one road connecting each pair of cities, and there is no road which connects the city with itself. It is possible that there is no way to get from one city to some other city using only these roads.
The road minister decided to make a reform in Berland and to orient all roads in the country, i.e. to make each road one-way. The minister wants to maximize the number of cities, for which the number of roads that begins in the city equals to the number of roads that ends in it.
The first line contains a positive integer t (1 ≤ t ≤ 200) — the number of testsets in the input.
Each of the testsets is given in the following way. The first line contains two integers n and m (1 ≤ n ≤ 200, 0 ≤ m ≤ n·(n - 1) / 2) — the number of cities and the number of roads in Berland.
The next m lines contain the description of roads in Berland. Each line contains two integers u and v (1 ≤ u, v ≤ n) — the cities the corresponding road connects. It's guaranteed that there are no self-loops and multiple roads. It is possible that there is no way along roads between a pair of cities.
It is guaranteed that the total number of cities in all testset of input data doesn't exceed 200.
Pay attention that for hacks, you can only use tests consisting of one testset, so t should be equal to one.
For each testset print the maximum number of such cities that the number of roads that begins in the city, is equal to the number of roads that ends in it.
In the next m lines print oriented roads. First print the number of the city where the road begins and then the number of the city where the road ends. If there are several answers, print any of them. It is allowed to print roads in each test in arbitrary order. Each road should be printed exactly once.
2
5 5
2 1
4 5
2 3
1 3
3 5
7 2
3 7
4 2
3
1 3
3 5
5 4
3 2
2 1
3
2 4
3 7
Understanding
大意:将一个无向图改为有向图,求入度=出度的点最多个数,并输出方案。
Analysis
首先确定度数为奇数的点一定不能成为答案。所以答案<=n-奇点
再考虑这些初始度数为奇数的点,由于是无向图,这样的点的个数显然是偶数个的(无向图度数之和为偶数,偶点之和为偶数,奇点之和也要为偶数,奇数×偶数=偶数,奇数×奇数=奇数)
Solution
脑补图的知识-欧拉回路(下面有听不懂的地方请点这里的链接)
法一(my):
构造法,欧拉回路,Fleury
建一个虚点(n+1),把奇点向其连边,所有节点为偶点,可以构成欧拉回路,删掉之前加的边对,偶点不会发生改变,且入度=出度,所以答案为偶点个数,方案用Fleury找一遍欧拉回路即可。
法二(%小胖犇)
Greedy,每次从奇点出发找一条链(找到自己继续),除了终点(奇点),经过的点都走过偶数次(进去,出来),直到没有度数。
法三(flow-O(n*m))
建图:把所有点任意定向(奇点之间配对连边)
设w=abs(ind[i]-oud[i])/2
如果ind[i]>oud[i],就从i向ED连容量为w的边
如果oud[i]>ind[i],就从ST向i连容量为w的边
跑下最大流,如果满流,就存在欧拉回路
因为我们的连边方式,肯定满流,肯定存在在欧拉回路,我们只要通过流量判定边的具体方向就好了
Code
// <E.cpp> - Mon Oct 3 19:17:39 2016
// This file is made by YJinpeng,created by XuYike's black technology automatically.
// Copyright (C) 2016 ChangJun High School, Inc.
// I don't know what this program is.
#include<bits/stdc++.h>
#pragma GCC push_options
#pragma GCC optimize ("O2")
#define IN inline
#define RG register
using namespace std;
const int MAXN=210;
inline int gi() {
register int w=0,q=0;register char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')q=1,ch=getchar();
while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar();
return q?-w:w;
}
set<int>s[MAXN];
vector<pair<int,int> >ans;
IN void dfs(RG int x){
while(s[x].size()){
RG int p=*s[x].begin();
s[x].erase(p);s[p].erase(x);
ans.push_back(make_pair(x,p));dfs(p);
}
}
int main()
{
freopen("E.in","r",stdin);
freopen("E.out","w",stdout);
int T=gi();
while(T--){
ans.clear();
int n=gi(),m=gi();
while(m--){
int x=gi(),y=gi();
s[x].insert(y),s[y].insert(x);
}
for(int i=1;i<=n;i++)
if(s[i].size()&1)s[n+1].insert(i),s[i].insert(n+1);
printf("%d
",n-s[n+1].size());
for(int i=1;i<=n;i++)dfs(i);
for(int i=0,to=ans.size();i<to;i++)
if(ans[i].first!=n+1&&ans[i].second!=n+1)
printf("%d %d
",ans[i].first,ans[i].second);
}
return 0;
}
LCF's Code
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define File(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout)
#define maxn 201
#define maxm 40010
using namespace std;
typedef long long llg;
int T,n,m,sa[maxm],sb[maxm],ls,du[maxn],ans;
bool g[maxn][maxn];
int getint(){
int w=0;bool q=0;
char c=getchar();
while((c>'9'||c<'0')&&c!='-') c=getchar();
if(c=='-') c=getchar(),q=1;
while(c>='0'&&c<='9') w=w*10+c-'0',c=getchar();
return q?-w:w;
}
void dfs(int u){
while(du[u]){
for(int i=1;i<=n;i++)
if(g[u][i]){
ls++; sa[ls]=u; sb[ls]=i;
du[u]--,du[i]--;
g[u][i]=g[i][u]=0;
u=i; break;
}
}
}
int main(){
//File("a");
T=getint();
while(T--){
ans=n=getint(); m=getint();
for(int i=1,x,y;i<=m;i++){
x=getint(); y=getint();
g[x][y]=g[y][x]=1;
du[x]++; du[y]++;
}
for(int i=1;i<=n;i++) ans-=du[i]&1;
printf("%d
",ans);
for(int i=1;i<=n;i++) if(du[i]&1) while(du[i]) dfs(i);
for(int i=1;i<=n;i++) while(du[i]) dfs(i);
for(int i=1;i<=ls;i++) printf("%d %d
",sa[i],sb[i]);
ls=0;
}
}
snowy_smile の Code(flow)
#include<stdio.h> #include<iostream> #include<string.h> #include<string> #include<ctype.h> #include<math.h> #include<set> #include<map> #include<vector> #include<queue> #include<bitset> #include<algorithm> #include<time.h> using namespace std; #define MS(x,y) memset(x,y,sizeof(x)) #define MC(x,y) memcpy(x,y,sizeof(x)) #define ls o<<1 #define rs o<<1|1 typedef long long LL; typedef unsigned long long UL; typedef unsigned int UI; template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; } template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; } const int N = 205, M = N * N * 20, Z = 1e9 + 7, inf = 0x3f3f3f3f; template <class T1, class T2>inline void gadd(T1 &a, T2 b) { a = (a + b) % Z; } int casenum, casei; int n, m; int ind[N], oud[N]; int ST, ED; int first[N]; int id; int w[M], cap[M], nxt[M]; void ins(int x, int y, int cap_) { w[++id] = y; cap[id] = cap_; nxt[id] = first[x]; first[x] = id; w[++id] = x; cap[id] = 0; nxt[id] = first[y]; first[y] = id; } int d[N]; bool bfs() { MS(d, -1); queue<int>q; q.push(ST); d[ST] = 0; while (!q.empty()) { int x = q.front(); q.pop(); for (int z = first[x]; z; z = nxt[z])if (cap[z]) { int y = w[z]; if (d[y] == -1) { d[y] = d[x] + 1; q.push(y); if (y == ED)return 1; } } } return 0; } int dfs(int x, int all) { if (x == ED)return all; int use = 0; for (int z = first[x]; z; z = nxt[z])if (cap[z]) { int y = w[z]; if (d[y] == d[x] + 1) { int tmp = dfs(y, min(cap[z], all - use)); cap[z] -= tmp; cap[z ^ 1] += tmp; use += tmp; if (use == all)break; } } if (use == 0)d[x] = -1; return use; } int dinic() { int ret = 0; while (bfs())ret += dfs(ST, inf); return ret; } int b[N], g; void solve() { int sum = 0; g = 0; for (int i = 1; i <= n; ++i) { if (abs(ind[i] - oud[i]) % 2 == 1)b[++g] = i; } for (int i = 1; i <= g; i += 2) { ins(b[i], b[i + 1], 1); ++oud[b[i]]; ++ind[b[i + 1]]; } for (int i = 1; i <= n; ++i) { int w = abs(ind[i] - oud[i]) / 2; if (ind[i] > oud[i]) { ins(i, ED, w); sum += w; } if (oud[i] > ind[i]) { ins(ST, i, w); } } dinic(); int ans = n - g; printf("%d ", ans); for (int i = 2; i <= 2 * m; i += 2) { if (cap[i] == 0)printf("%d %d ", w[i], w[i ^ 1]); else printf("%d %d ", w[i ^ 1], w[i]); } } int main() { scanf("%d", &casenum); for (casei = 1; casei <= casenum; ++casei) { scanf("%d%d", &n, &m); ST = 0; ED = n + 1; MS(first, 0); id = 1; for (int i = 1; i <= n; ++i)oud[i] = ind[i] = 0; for (int i = 1; i <= m; ++i) { int x, y; scanf("%d%d", &x, &y); ++oud[x]; ++ind[y]; ins(x, y, 1); } solve(); } return 0; }
F. st-Spanning Tree
You are given an undirected connected graph consisting of n vertices and m edges. There are no loops and no multiple edges in the graph.
You are also given two distinct vertices s and t, and two values ds and dt. Your task is to build any spanning tree of the given graph (note that the graph is not weighted), such that the degree of the vertex s doesn't exceed ds, and the degree of the vertex t doesn't exceed dt, or determine, that there is no such spanning tree.
The spanning tree of the graph G is a subgraph which is a tree and contains all vertices of the graph G. In other words, it is a connected graph which contains n - 1 edges and can be obtained by removing some of the edges from G.
The degree of a vertex is the number of edges incident to this vertex.
The first line of the input contains two integers n and m (2 ≤ n ≤ 200 000, 1 ≤ m ≤ min(400 000, n·(n - 1) / 2)) — the number of vertices and the number of edges in the graph.
The next m lines contain the descriptions of the graph's edges. Each of the lines contains two integers u and v (1 ≤ u, v ≤ n, u ≠ v) — the ends of the corresponding edge. It is guaranteed that the graph contains no loops and no multiple edges and that it is connected.
The last line contains four integers s, t, ds, dt (1 ≤ s, t ≤ n, s ≠ t, 1 ≤ ds, dt ≤ n - 1).
If the answer doesn't exist print "No" (without quotes) in the only line of the output.
Otherwise, in the first line print "Yes" (without quotes). In the each of the next (n - 1) lines print two integers — the description of the edges of the spanning tree. Each of the edges of the spanning tree must be printed exactly once.
You can output edges in any order. You can output the ends of each edge in any order.
If there are several solutions, print any of them.
3 3
1 2
2 3
3 1
1 2 1 1
Yes
3 2
1 3
Understanding
给你一个图,求一个生成树,使得s的度数不超过ds,t的度数不超过dt,按输入顺序输出方案
Solution
Greedy+并查集.
先将不含s和t的其他点组成连通块。
然后接下来就是用s,t将构成树。
首先每个连通块只有3种情况:
- 与s或t相连,就只能连起,ds--||dt--
- 与s和t都相连,加入队列中之后处理
- 都不相连"No"
考虑将s与t连起,并且dsdt最大
如果有一个块与st相连,那么连起。否则,就看是不是已经连通,再否则就看s可不可以与t相连,再否则"No"
接下来因为s与t相连,其它的块就只需要找s||t连。
最后ds||dt <0 "No" else 输出结果。
Code
notice //this的地方
// <F.cpp> - Mon Oct 3 21:43:10 2016 // This file is made by YJinpeng,created by XuYike's black technology automatically. // Copyright (C) 2016 ChangJun High School, Inc. // I don't know what this program is. #include <iostream> #include <vector> #include <algorithm> #include <cstring> #include <cstdio> #include <cstdlib> #include <cmath> #define MOD 1000000007 #define INF 1e9 #define IN inline #define RG register using namespace std; typedef long long LL; typedef long double LB; const int MAXN=200010; const int MAXM=400010<<1; inline int max(int &x,int &y) {return x>y?x:y;} inline int min(int &x,int &y) {return x<y?x:y;} inline LL gi() { register LL w=0,q=0;register char ch=getchar(); while((ch<'0'||ch>'9')&&ch!='-')ch=getchar(); if(ch=='-')q=1,ch=getchar(); while(ch>='0'&&ch<='9')w=w*10+ch-'0',ch=getchar(); return q?-w:w; } int fr[MAXN],f[MAXN];int te;bool k[MAXM]; int to[MAXM],ne[MAXM],ev[MAXM],eu[MAXM],w[MAXM];vector<int>a[MAXN],b,c,d; IN void link(int u,int v,int p){ to[++te]=v;ne[te]=fr[u];fr[u]=te;w[te]=p; to[++te]=u;ne[te]=fr[v];fr[v]=te;w[te]=p; } IN int find(int x){return x==f[x]?x:f[x]=find(f[x]);} IN void pri(){printf("No");exit(0);} int main() { freopen("F.in","r",stdin); freopen("F.out","w",stdout); int n=gi(),m=gi(); for(int i=1;i<=m;i++){ eu[i]=gi();ev[i]=gi(); link(eu[i],ev[i],i); } int s=gi(),t=gi(),ds=gi(),dt=gi(); for(int i=1;i<=n;i++)f[i]=i;te=0; for(int i=1;i<=n;i++){ if(i==s||i==t)continue; for(int o=fr[i];o;o=ne[o]){ if(to[o]==s||to[o]==t)continue; f[i]=find(i);f[to[o]]=find(to[o]); if(f[i]!=f[to[o]])k[w[o]]=1,f[f[i]]=f[to[o]]; } } for(int i=1;i<=n;i++){ find(i);//this a[f[i]].push_back(i); }//this TLE→n^2 for(int i=1;i<=n;i++){ if(i==s||i==t||f[i]!=i)continue;int be1=0,be2=0; for(int j,kk=0,g=a[f[i]].size();j=a[f[i]][kk],kk<g;kk++) if(f[j]==i){ for(int o=fr[j];o;o=ne[o]) if(to[o]==s)be1=w[o];else if(to[o]==t)be2=w[o]; if(be1&&be2)break; } if(!be1&&!be2)pri();//this if(be1&&be2)b.push_back(be1),c.push_back(be2); else{ if(be1)ds--,f[i]=s,k[be1]=1; if(be2)dt--,f[i]=t,k[be2]=1; } } if(b.size())ds--,dt--,k[b[0]]=1,k[c[0]]=1;else {//this te=find(1); for(int i=1;i<=n;i++)if(find(i)!=te){te=-1;break;}//this if(te==-1){//this te=0; for(int i=fr[s];i;i=ne[i]) if(to[i]==t){te=1;k[w[i]]=1;break;} if(!te)pri();ds--;dt--;f[s]=t; } } for(int to=b.size(),i=1;i<to;i++){ if(ds){ds--;k[b[i]]=1;continue;} dt--;k[c[i]]=1; }//this if(ds<0||dt<0)pri(); printf("Yes "); for(int i=1;i<=m;i++)if(k[i])printf("%d %d ",eu[i],ev[i]);//this return 0; }