题目描述
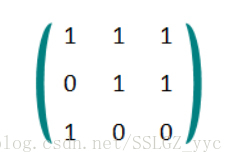
小X最近迷上了矩阵,他定义了一个对于一种特殊矩阵的特征函数G。对于N*N的矩阵A,A的所有元素均为0或1,则G(A)等于所有A[i][j]*A[j][i]的和对2取余之后的结果。举一个例子:
对于上图这个3 * 3矩阵A,G(A)=(1 * 1 + 1 * 0 + 1 * 1 + 0 * 1 + 1 * 1 + 1 * 0 + 1 * 1 + 0 * 1 + 0 * 0) mod 2=0
当然询问一个矩阵的G值实在是太简单了。小X在给出一个N*N矩阵的同时将给你Q个操作,操作描述如下:
操作1:形如一个整数1和一个整数x,表示将第x行的元素全部“翻转”。
操作2:形如一个整数2和一个整数x,表示将第x列的元素全部“翻转”。
操作3:形如一个整数3,表示询问当前矩阵的特征值G。
“翻转”的定义为将1变成0,将0变成1。
输入
第1行:两个正整数N,Q。 N表示矩阵的行数(列数),Q表示询问的个数。
接下来N行:一个N*N的矩阵A,0<=A[i][j]<=1。
接下来Q行:Q个操作。
输出
一行若干个数,中间没有空格,分别表示每个操作的结果(操作1和操作2不需要输出)。
输入样例
3 12
1 1 1
0 1 1
1 0 0
3
2 3
3
2 2
2 2
1 3
3
3
1 2
2 1
1 1
3
输出样例
01001
说明
30% N<=100, Q<=10^5
100% N<=1,000, Q <=5*10^5
.
.
.
.
.
分析
我们可以发现:a[i][j]*a[j][i]+a[j][i]*a[i][j] 对于答案毫无意义
因此,答案为矩阵的 右上至左下 的对角线的G值
对于一个操作,无论它是在哪一行哪一列,它都会对线上的一个值(只有一个)进行影响,那么每次只需将答案取反即可。
.
.
.
.
.
程序:
#include<iostream>
#include<cstdio>
using namespace std;
inline int read()
{
int s=0,w=1;
char ch=getchar();
while (ch<'0'||ch>'9')
{
if (ch=='-') w=-1;
ch=getchar();
}
while (ch>='0'&&ch<='9')
{
s=s*10+ch-'0';
ch=getchar();
}
return s*w;
}
int main()
{
int n,q;
bool ans=0;
n=read();
q=read();
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
{
int x;
x=read();
if (i==j) ans=(ans+x)%2;
}
for (int i=1;i<=q;i++)
{
int x=read();
if (x==3) printf("%d",ans); else
{
int y=read();
ans=ans^1;
}
}
return 0;
}