深度优先搜索

Depth First Search

Depth-first search (DFS) follows the strategy to search ”deeper” in the graph whenever possible. In DFS, edges are recursively explored out of the most recently discovered vertex vv that still has unexplored edges leaving it. When all of vv's edges have been explored, the search ”backtracks” to explore edges leaving the vertex from which vv was discovered.

This process continues until all the vertices that are reachable from the original source vertex have been discovered. If any undiscovered vertices remain, then one of them is selected as a new source and the search is repeated from that source.

DFS timestamps each vertex as follows:

• d[v]d[v] records when vv is first discovered.
• f[v]f[v] records when the search finishes examining vv’s adjacency list.

Write a program which reads a directed graph G=(V,E)G=(V,E) and demonstrates DFS on the graph based on the following rules:

• GG is given in an adjacency-list. Vertices are identified by IDs 1,2,...n1,2,...n respectively.
• IDs in the adjacency list are arranged in ascending order.
• The program should report the discover time and the finish time for each vertex.
• When there are several candidates to visit during DFS, the algorithm should select the vertex with the smallest ID.
• The timestamp starts with 1.

Input

In the first line, an integer nn denoting the number of vertices of GG is given. In the next nn lines, adjacency lists of uu are given in the following format:

uu kk v1v1 v2v2 ... vkvk

uu is ID of the vertex and kk denotes its degree. vivi are IDs of vertices adjacent to uu.

Output

For each vertex, print idid, dd and ff separated by a space character in a line. idid is ID of the vertex, dd and ffis the discover time and the finish time respectively. Print in order of vertex IDs.

Constraints

• 1≤n≤1001≤n≤100

Sample Input 1

4
1 1 2
2 1 4
3 0
4 1 3

Sample Output 1

1 1 8
2 2 7
3 4 5
4 3 6

Sample Input 2

6
1 2 2 3
2 2 3 4
3 1 5
4 1 6
5 1 6
6 0

Sample Output 2

1 1 12
2 2 11
3 3 8
4 9 10
5 4 7
6 5 6

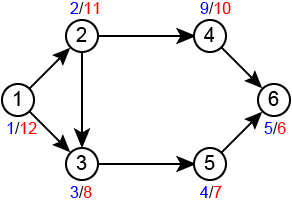
This is example for Sample Input 2 (discover/finish)

Reference

Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.

题意：深度优先搜索遍历图，记录每个节点第一次被访问的时间和调查完这个节点的邻接表之后的时间(结束访问时刻)

基础的DFS

代码：

#define _CRT_SECURE_NO_DEPRECATE
#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<cstring>
#include<set>
#include<string>
using namespace std;
typedef long long ll;
const int N_MAX = 300;
vector<int>G[N_MAX];
int n;
int Start[N_MAX], End[N_MAX];
int Time;
bool vis[N_MAX];
void dfs(int cur) {//当前走到cur点,time是当前的时间
    Start[cur] = ++Time;
    vis[cur] = true;
    int size = G[cur].size();
    for (int i = 0; i < size;i++) {
        int v = G[cur][i];
        if (vis[v] == false) {//这个节点还没到达过
            dfs(v);
        }
      }
    End[cur] = ++Time;//访问结束
}

int main() {
    while (scanf("%d",&n)!=EOF) {
        Time = 0;
        memset(vis, 0, sizeof(vis));
        for (int i = 0; i < n;i++) {
            int from, num;
            scanf("%d%d",&from,&num);
            from--;
            for (int j = 0; j < num;j++) {
                int to;
                scanf("%d",&to);
                to--;
                if(to!=from)G[from].push_back(to);
            }
        }
        
        for (int i = 0; i < n;i++) {
            if(!vis[i])dfs(i);
        }
        
        for (int i = 0; i < n;i++) {
            printf("%d %d %d
",i+1,Start[i],End[i]);
        }
        for (int i = 0; i < n;i++) {
            G[i].clear();
        }

    }

    return 0;
}