2017—2018 20162329 张旭升 实验报告：树

实验二：数

课程：程序设计与数据结构
班级： 1623
姓名： 张旭升
学号：20162329
指导教师：娄嘉鹏 王志强
实验日期：10月23日

实验密级： 非密级
预习程度： 已预习

必修/选修： 必修
实验序号： cs_29

实验名称：二叉树、树型结构的实现及应用

1. 实现二叉树

2. 中序先序序列构造二叉树

3. 决策树

4. 表达式树

5. 实现二叉查找树

6. 红黑树源码分析

实验要求

---

1.没有Linux基础的同学建议先学习《Linux基础入门（新版）》《Vim编辑器》 课程

2. 完成实验、撰写实验报告，实验报告以博客方式发表在博客园，注意实验报告重点是 运行结果，遇到的问题(工具查找，安装，使用，程序的编辑，调试，运行等)、解决 办法（空洞的方法如“查网络”、“问同学”、“看书”等一律得0分）以及分析（从中可 以得到什么启示，有什么收获，教训等）。报告可以参考范飞龙老师的指导

3. 严禁抄袭，有该行为者实验成绩归零，并附加其他惩罚措施。

---

一、实现二叉树

参考教材p375,完成链树LinkedBinaryTree的实现（getRight,contains,toString,preorder,postorder）
用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试，提交测试代码运行截图，要全屏，包含自己的学号信息
课下把代码推送到代码托管平台

书上已经帮我们创建好了二叉树的接口，并帮我们已经实现了部分方法，我们只需要实现以下方法就可以了：

public LinkedBinaryTree<T> getRight() throws Exception {     //获取右子树的方法
     if (root == null)
         throw new Exception ("Get left operation "
                 + "failed. The tree is empty.");

     LinkedBinaryTree<T> result = new LinkedBinaryTree<>();
     result.root = root.getRight();
     return result;
 }


 public boolean contains (T target) throws Exception {     //查找某元素是否存在的方法
    BTNode<T> node = null;
    boolean result = true;
     if (root != null)
         node = root.find(target);
    if(node == null)
        result = false;
     return result;
 }

 public boolean isEmpty() {    //判断树是否为空的方法
     boolean result = false;
     if(root == null)
         result = true;
     return result;
 }

 public String toString() {     //树的打印方法
     ArrayList<T> list = null;
     try {
         list = levelorder();
     } catch (Exception e) {
         e.printStackTrace();
     }
     String result = "";
    for(T i : list){
        result += i + "	";
    }
    return result;
 }

 public  ArrayList<T> preorder() {     //树的先序遍历方法
    ArrayList<T> list = new ArrayList<>();

    if(root!=null)
        root.preorder(list);
    return list;
 }

 public  ArrayList<T> postorder() {    //树的后序遍历的方法
     ArrayList<T> list = new ArrayList<>();

     if(root!=null)
         root.postorder(list);
     return list;
 }

源码链接

测试截图：

二、中序先序序列构造二叉树

基于LinkedBinaryTree，实现基于（中序，先序）序列构造唯一一棵二㕚树的功能，比如教材P372，给出HDIBEMJNAFCKGL和ABDHIEJMNCFGKL,构造出附图中的树
用JUnit或自己编写驱动类对自己实现的功能进行测试，提交测试代码运行截图，要全屏，包含自己的学号信息
课下把代码推送到代码托管平台

1.实现思路

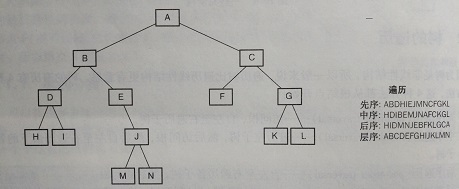
如图，先序遍历出的先序序列的第一个元素就是整个树的根结点，而中序序列恰好是以根结点为界，将树的左右子树都分在了根结点的两边，而我们就可以用这样的思路来用两个序列对树进行重构，具体操作就是，每次在中序序列中查找先序序列中第一个元素的位置，然后以该元素为界在中序序列中将该元素的左边定为其左子树，右边定为其右子树，然后以先左后右的顺序对左右子树再进行上面的操作，直到在中序序列中只有先序序列的第一个元素时结束，该方法可以用递归的思想进行实现。

实现代码：

public BTNode<T> reConstructBinaryTree(T [] pre,T [] in) {
    BTNode root=new BTNode(pre[0]);//前序的第一个数定为根
    int len=pre.length;
    //当只有一个数的时候
    if(len==1){
        root.left=null;
        root.right=null;
        return root;
    }
    //找到中序中的根位置
    T rootval= (T) root.getElement();
    int i;
    for(i=0;i<len;i++){
        if(root.getElement()==in[i])
            break;
    }
    //创建左子树
    if(i>0){
        T[] pr=(T[])new Object[i];
        T[] ino=(T[])new Object[i];
        for(int j=0;j<i;j++){
            pr[j]=pre[j+1];
        }
        for(int j=0;j<i;j++){
            ino[j]=in[j];
        }
        root.left=reConstructBinaryTree(pr,ino);
    }else{
        root.left=null;
    }
    //创建右子树
    if(len-i-1>0){
        T[] pr=(T[])new Object[len-i-1];
        T[] ino=(T[])new Object[len-i-1];
        for(int j=i+1;j<len;j++){
            ino[j-i-1]=in[j];
            pr[j-i-1]=pre[j];
        }
        root.right=reConstructBinaryTree(pr,ino);
    }else{
        root.right=null;
    }
    return root;
}

2.源码链接

3.测试截图：

三、决策树

完成PP16.6
提交测试代码运行截图，要全屏，包含自己的学号信息
课下把代码推送到代码托管平台

1.实现思路：

二叉树中树的一个结点只能有两个左右子树，又因为树多以链式结构构建，所以以某个结点为根的话下面将分出多条链，我们可以利用链的环环相扣的模式来构建决策或者测试程序。具体思路就是在根结点中设置一个问题，然后用户可以根据问题回答对或错，分别对应左右子树中的下一个问题，直到所有问题回答完毕后，最后一个结点会输出一个结论（决策）。

代码实现：

public questionGame() {
    String e1 = "是动物吗？";
    String e2 = "它有没有长尾巴？";
    String e3 = "会游泳吗？";
    String e4 = "能直立行走吗？";
    String e5 = "结果：人！";
    String e6 = "结果：昆虫！";
    String e7 = "结果：鱼！";
    String e8 = "结果：猫！";
    String e9 = "很大吗？";
    String e10 = "结果：树！";
    String e11 = "带刺吗？";
    String e12 = "结果：玫瑰！";
    String e13 = "结果：花";

    LinkedBinaryTree<String> n1, n2, n3, n4, n5, n6, n7, n8, n9, n10, n11, n12, n13;
    n12 = new LinkedBinaryTree<>(e12);
    n13 = new LinkedBinaryTree<>(e13);
    n11 = new LinkedBinaryTree<>(e11,n12,n13);

    n10 = new LinkedBinaryTree<>(e10);
    n9 = new LinkedBinaryTree<>(e9,n10,n11);

    n8 = new LinkedBinaryTree<>(e8);
    n7 = new LinkedBinaryTree<>(e7);
    n3 = new LinkedBinaryTree<>(e3,n7,n8);

    n5 = new LinkedBinaryTree<>(e5);
    n6 = new LinkedBinaryTree<>(e6);
    n4 = new LinkedBinaryTree<>(e4,n5,n6);

    n2 = new LinkedBinaryTree<>(e2,n3,n4);

    tree = new LinkedBinaryTree<>(e1,n2,n9);
}
public void Game() throws Exception {
    Scanner scan = new Scanner(System.in);

    while (tree.size()>1){
        System.out.println(tree.getRootElement());
        String result = scan.nextLine();
        if(result.equalsIgnoreCase("Y"))
            tree = tree.getLeft();
        else if(result.equalsIgnoreCase("N"))
            tree = tree.getRight();
    }
    System.out.println(tree.getRootElement());
}

2.源码链接

3.测试截图：

四、表达式树

完成PP16.8
提交测试代码运行截图，要全屏，包含自己的学号信息
课下把代码推送到代码托管平台

1.实现思路：

在计算机中对于运算中缀表达式是无法明确计算的，因为当式子过长时，总会出现运算优先级的问题，而这种判断计算机是不具备的，所以在计算机表达式的运算中常常将中缀表达式转换为后缀表达式，之前我们用栈的数据结构实现过该功能，现在我们用树来实现。具体思路是，当我们获取到一个中缀表达式时，我们的思路就是先计算优先级高的（即乘除和括号），然后在全是同样低优先级（即加减）的情况下再顺序计算，我们将获取到的表达式中的数字和操作符分开储存在两个列表里，数是以结点的形式储存，而操作符是以数据的方式储存，注意：操作符只存储加或减，当遇到乘除号时就将它前面和后面的数设为它的左右叶子结点存在数的列表里，知道表达式读取完毕，就顺序的从操作符列表取一个符号然后就吧数列表的前两个元素设为它的子节点，存在数列表的第一个，一直到操作符列表为空为止。

代码实现：

public BTNode creatTree(String str){
    StringTokenizer tokenizer = new StringTokenizer(str);
    String token;
    ArrayList<String> operList = new ArrayList<>();

    ArrayList<LinkedBinaryTree> numList = new ArrayList<>();
    while (tokenizer.hasMoreTokens()){
        token = tokenizer.nextToken();
        if(token.equals("(")){
            String str1 = "";
            while (true){
                token = tokenizer.nextToken();
                if (!token.equals(")"))
                    str1 += token + " ";
                else break;
            }
            LinkedBinaryTree S = new LinkedBinaryTree();
            S.root = creatTree(str1);
            numList.add(S);
        }
        if(as(token)){
            operList.add(token);
        }else if(md(token)){
            LinkedBinaryTree left = numList.remove(numList.size()-1);
            String A = token;
            token = tokenizer.nextToken();
            if(!token.equals("(")) {
                LinkedBinaryTree right = new LinkedBinaryTree(token);
                LinkedBinaryTree node = new LinkedBinaryTree(A, left, right);
                numList.add(node);
            }else {
                String str1 = "";
                while (true){
                    token = tokenizer.nextToken();
                    if (!token.equals(")"))
                        str1 += token + " ";
                    else break;
                }
                LinkedBinaryTree S = new LinkedBinaryTree();
                S.root = creatTree(str1);
                LinkedBinaryTree node = new LinkedBinaryTree(A,left,S);
                numList.add(node);
            }
        }else
            numList.add(new LinkedBinaryTree(token));
    }
    while(operList.size()>0){
        LinkedBinaryTree left = numList.remove(0);
        LinkedBinaryTree right = numList.remove(0);
        String oper = operList.remove(0);

        LinkedBinaryTree node = new LinkedBinaryTree(oper,left,right);
        numList.add(0,node);
    }
    root = (numList.get(0)).root;

    return root;
}

private boolean as(String token){
    return (token.equals("+")||
            token.equals("-"));
}

private boolean md(String token){
    return (token.equals("*")||
            token.equals("/"));
}

2.源码链接

3.测试截图：

五、实现二叉查找树

完成PP17.1
提交测试代码运行截图，要全屏，包含自己的学号信息
课下把代码推送到代码托管平台

1.实现思路：

与第一个实验一样，书上已经给我定义好了接口类，并实现了部分方法，我们只需要对缺少的方法进行补充就可以了。

代码实现：

public T findMin() {      //查找最小值的方法
    BTNode<T> r =  root;
    while (r.getLeft() != null)
        r = r.getLeft();
    return  r.getElement();
 }
 public T findMax() {      //查找最大值的方法
     BTNode<T> r =  root;
    while (r.getRight() != null)
        r = r.getRight();
    return  r.getElement();
 }

2.源码链接

3.测试截图：

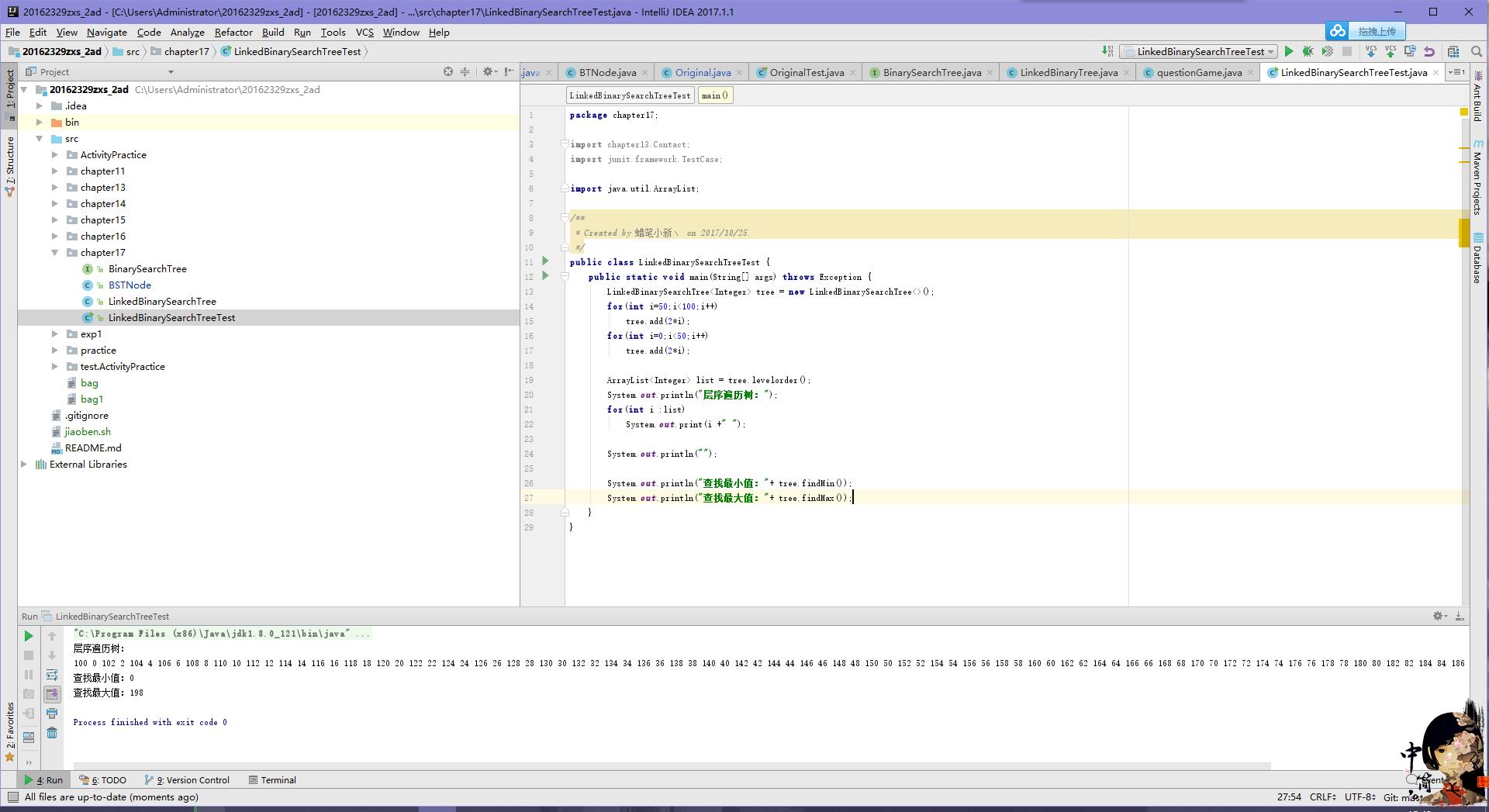
六、红黑树源码分析

1.集合一般提供两种常规的Map实现，一种是HashMap,另一种是TreeMap，下面将具体分析这两种map的实现：

HashMap：基于哈希表实现。使用HashMap要求添加的键类明确定义了hashCode()和equals()[可以重写hashCode()和equals()]，为了优化HashMap空间的使用，您可以调优初始容量和负载因子。

(1)HashMap(): 构建一个空的哈希映像
(2)HashMap(Map m): 构建一个哈希映像，并且添加映像m的所有映射
(3)HashMap(int initialCapacity): 构建一个拥有特定容量的空的哈希映像
(4)HashMap(int initialCapacity, float loadFactor): 构建一个拥有特定容量和加载因子的空的哈希映像

TreeMap：基于红黑树实现。TreeMap没有调优选项，因为该树总处于平衡状态。

(1)TreeMap():构建一个空的映像树
(2)TreeMap(Map m): 构建一个映像树，并且添加映像m中所有元素
(3)TreeMap(Comparator c): 构建一个映像树，并且使用特定的比较器对关键字进行排序
(4)TreeMap(SortedMap s): 构建一个映像树，添加映像树s中所有映射，并且使用与有序映像s相同的比较器排序

2.HashMap通过hashcode对其内容进行快速查找，而 TreeMap中所有的元素都保持着某种固定的顺序，

如果你需要得到一个有序的结果你就应该使用TreeMap（HashMap中元素的排列顺序是不固定的）。

3.线程方面：HashMap 非线程安全 TreeMap 线程安全

在Java里，线程安全一般体现在两个方面：
<1多个thread对同一个java实例的访问（read和modify）不会相互干扰，它主要体现在关键字synchronized。如ArrayList和Vector，HashMap和Hashtable
（后者每个方法前都有synchronized关键字）。如果你在interator一个List对象时，其它线程remove一个element，问题就出现了。

<2每个线程都有自己的字段，而不会在多个线程之间共享。它主要体现在java.lang.ThreadLocal类，而没有Java关键字支持，如像static、transient那样。

4.AbstractMap抽象类和SortedMap接口

AbstractMap抽象类：(HashMap继承AbstractMap)覆盖了equals()和hashCode()方法以确保两个相等映射返回相同的哈希码。如果两个映射大小相等、包含同样的键且每个键在这两个映射中对应的值都相同，则这两个映射相等。映射的哈希码是映射元素哈希码的总和，其中每个元素是Map.Entry接口的一个实现。因此，不论映射内部顺序如何，两个相等映射会报告相同的哈希码。
SortedMap接口：（TreeMap继承自SortedMap）它用来保持键的有序顺序。SortedMap接口为映像的视图(子集)，包括两个端点提供了访问方法。除了排序是作用于映射的键以外，处理SortedMap和处理SortedSet一样。添加到SortedMap实现类的元素必须实现Comparable接口，否则您必须给它的构造函数提供一个Comparator接口的实现。TreeMap类是它的唯一一份实现。

5.两种常规Map性能

HashMap：适用于在Map中插入、删除和定位元素。
Treemap：适用于按自然顺序或自定义顺序遍历键(key)。

6.总结：HashMap通常比TreeMap快一点(树和哈希表的数据结构使然)，建议多使用HashMap，在需要排序的Map时候才用TreeMap

• 它的左、右子树也分别为排序二叉树。