Pylab的使用
学习使用Python进行科学计算,然而很难找到简单实用,又循序渐进的例子。正好手边有一本《Matlab可视化大学物理学》,里面的例子非常清晰地解释了Matlab在物理学中的应用。重新使用Python实现这些例子,学习了Python,又学习了科学计算思想,一举两得。
1.1Pylab简介
pylab是Matplotlib和Ipython提供的一个模块,提供了类似Matlab的语法,在启动Ipython时可以使用--pylab启动,它相当于导入了如下库:
import numpy
import matplotlib
from matplotlib import pylab, mlab, pyplot
np = numpy
plt = pyplot
from IPython.display import display
from IPython.core.pylabtools import figsize, getfigs
from pylab import *
from numpy import *
1.2简单应用
1.2.1画圆
(cos^2x+sin^2x = 1)
n = 10
#生成50个元素的行向量
phi = linspace(0, 2*pi)
# 此时绘制x,y可以得到一个圆
x = cos(phi)
y = sin(phi)
for i in range(1,n):
for j in range(1,i):
#(绘图 1)
plot(x + 2 * j, y - 2 * j)
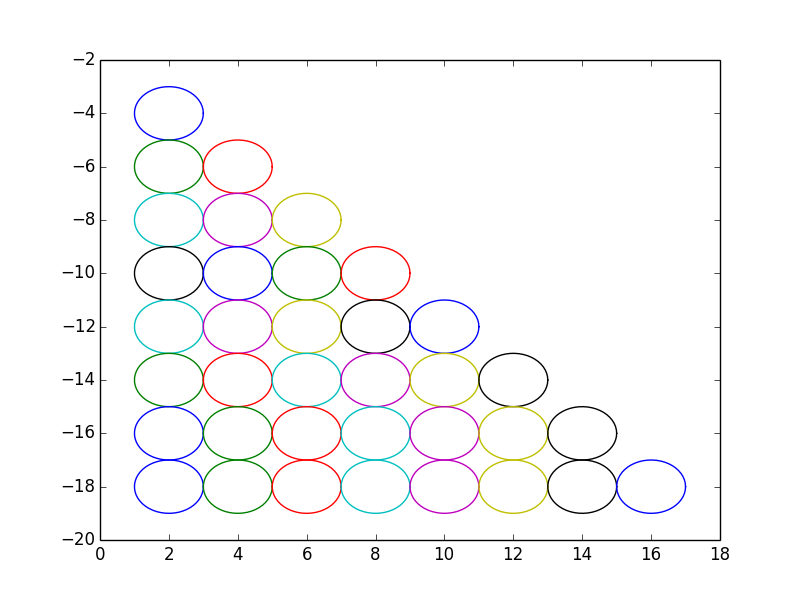
如果将绘图1指令改为:
plot(x + 2*j -i, y - sqrt(3) * i)
可以绘制出交错堆叠。
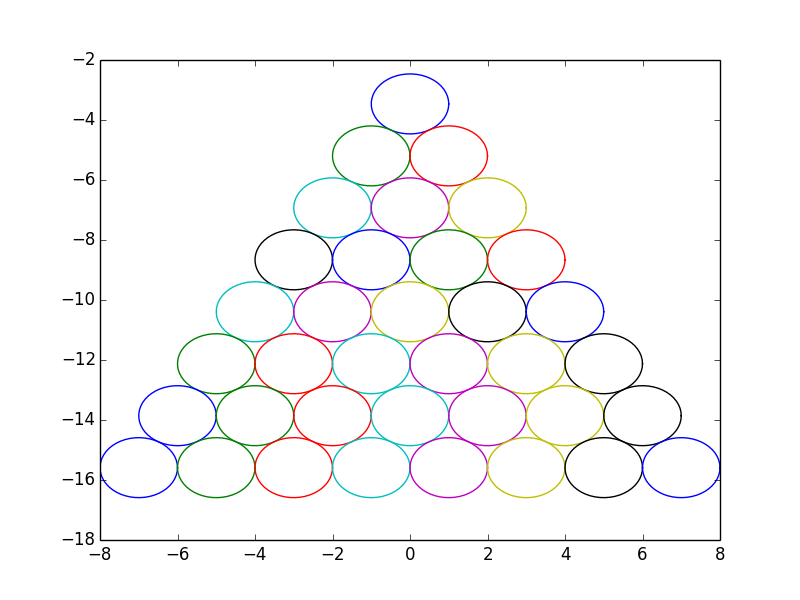
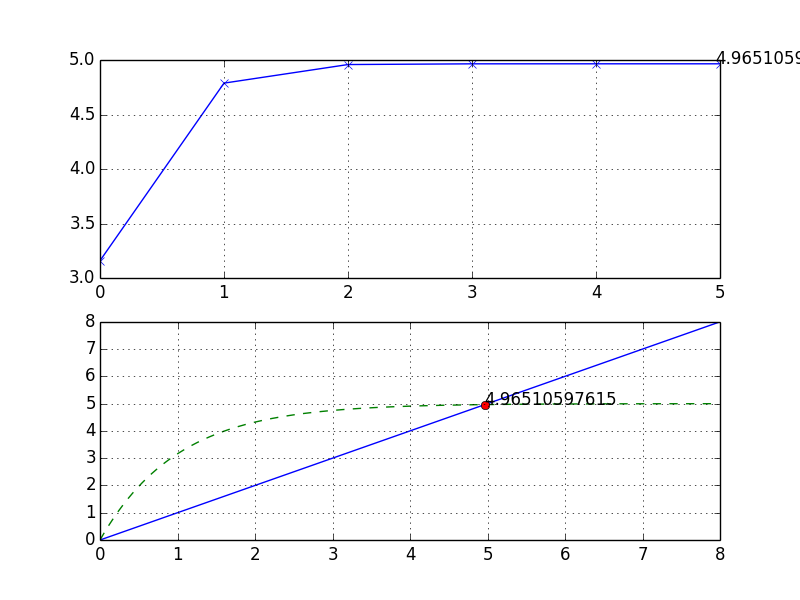
1.2.2不定循环(indefinite loop)与超越方程(transcentental equation)
超越方程在数学与物理中十分常见,然而并没有确定的解析解法。需要使用数值解或图形解。
在黑体辐射中,峰值波长与温度成反比,比例系数为维恩常数(Wien's displacement law)。根据普朗克公式求维恩常数时,产生如下的超越方程:
[x+5(e^{-x}-1)=0
]
超越方程的解也应该是下面一条直线和指数函数曲线的交点:
[y=x , y = 5[1-e^{(-x)}]
]
对于数值计算而言,可以使用牛顿法求解以上方程。
x0 = 1 #iteration method
xx = []
while True:
x = 5 * (1 - exp( - x0))
xx.append(x)
if len(xx) > 1000:
break
if abs(x0 - x) < 0.0001:
break
x0 = x
subplot(211)#绘图部分,首先绘制iteration method求得的解
plot(xx,"x-")
grid()
text(x0, x0, str(x0))
subplot(212)#然后绘制图形解法的解
nx = arange(0,8,0.01)
plot(nx, nx, nx, 5*(1 - exp( -nx)), "--")
plot(x0, x0, "o")
text(x0, x0, str(x0))
grid()
show()