传送门
不错的题8(不知为啥到我手上特判的贼多)
简述题意:给你(n)个结点,每个结点有一个初始值(a_i),以及目标值,并且给定两种边((u_i,v_i)),第一种边使(a_{u_i})和(a_{v_i})同时加一,第二种边使(a_{u_i})和(a_{v_i})一个加一,一个减一。问最后能否使所有结点变成目标状态。
以下是我在当时测试时的思路。
首先到达最终的目标,也就是说使得对应的结点的数值增加(b_i-a_i),让每个结点表示这个值,问题就转化成了能否使所有的数值变成(0)了。
看两种边有什么特别之处。一下子看第一种边没发现什么,第二种边相当于可以将一个结点上的部分数字“传输”到与其相邻的结点之处,稍加拓展不难发现第二种边构成的连通图中,任意一个结点可将其数字传到另外的任意一个结点,如下图:

这样的意义在于:能自由分配连通图中所有的数值(都转移到一个结点、或者分配到若干个点),可以无需关心具体的分配情况,于是将他们缩成一个点,其权值为(sum w_i)。
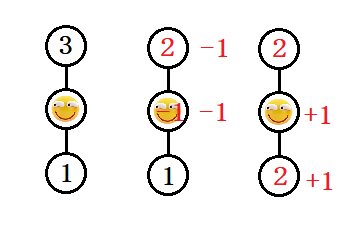
这样就只剩下第一种边了。它们只有两种情况:(1)连接两个连通块(即缩点后连接两个点),这个的影响是让连接的两个缩点加或减相等的数字;(2)在某个连通块内,这个的影响是让这个缩点加或减一个偶数。我们还是用传输的思想,手算会发现(1)可以将某个点的数值隔两个点传过去,如下图:
对于缩过点的图,每个由第一种边构成的连通块,仔细想想会发现:如果这个连通块不能被黑白染色,则一定可以将数值放到某一个奇环上的一个点,同样这个也是可逆的,故一个数一定可以借助奇环把另一个相等的数消除;反之,如果能被黑白染色,显然可以将所有黑点的数值和白点的数值移到一条相邻的边,然后再一起消掉。没有(2)情况的干扰下,对于每个连通块,按照上面分类讨论,如果仍然不能完全消除,那显然输出( ext{NO})了。所有的都满足才输出( ext{YES})。
加上(2),其实就是可以对权值调整,在有(2)的连通块下,不一定要全部消除,只要消到能剩余(2)的倍数就好啦(可以依靠这样的边在连通块内部就消除掉)。于是我们整理一下:
1、根据第二种边求出所有的连通块并且缩起来;
2、根据第一种边求出所有的连通块,对每个连通块判断能否黑白染色,如果能就染色,求出所有黑点和白点的权值和,顺便看看有没有情况(2);
3、检查该连通块是否满足要求:a.如果不能黑白染色,只需要看这个连通块的权值和是不是偶数;b.如果能,判断黑点权值和和白点权值和的关系,如果有(2),那么只需差为偶数即可;否则必须相等(具体详见上文);
4、如果所有的连通块都能通过测试,输出( ext{YES});否则输出( ext{NO})。
时间复杂度( ext{O}(Tn))。可以通过。
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define min(a, b) (a) < (b) ? (a) : (b)
#define max(a, b) (a) > (b) ? (a) : (b)
#define rep(i, a, b) for (int i = a, i##end = b; i <= i##end; ++i)
#define per(i, a, b) for (int i = a, i##end = b; i >= i##end; --i)
#define rep0(i, a) for (int i = 0, i##end = a; i < i##end; ++i)
#define per0(i, a) for (int i = a-1; ~i; --i)
#define chkmax(a, b) a = max(a, b)
#define chkmin(a, b) a = min(a, b)
inline int read() {
int w = 0, f = 1; char c;
while (!isdigit(c = getchar())) c == '-' && (f = 1);
while (isdigit(c)) w = w*10+(c^48), c = getchar();
return w * f;
}
const int maxn = 114514;
int n, m;
std::vector<int> G1[maxn], G2[maxn], G[maxn];
int id[maxn], delta[maxn], tag[maxn], col[maxn], idcnt = 0;
// id为连通块编号、delta表示a[i]-b[i](相反亦可),tag表示有没有(2)情况,col为染色情况,idcnt表示连通块个数
ll sum[maxn]; // 每个连通块内的权值总和
void dfs(int u) {
sum[id[u] = idcnt] += delta[u]; // 标记连通块并且合并权值
rep0(i, G2[u].size()) if (!id[G2[u][i]]) dfs(G2[u][i]);
}
int paint(int u, ll &white, ll &black, int &flag) {
int ok = 1; // 表示是否染色成功
col[u] == 1 ? white += sum[u] : black += sum[u]; flag |= tag[u]; // 计算white,black点的权值
rep0(i, G[u].size()) {
int v = G[u][i];
if (col[v]) { if (col[v] == col[u]) ok = 0; continue; } // 失败
col[v] = 3-col[u];
ok &= paint(v, white, black, flag);
}
return ok;
}
int main() {
for (int T = read(); T; T--) {
n = read(), m = read();
rep(i, 1, n) delta[i] = read();
rep(i, 1, n) delta[i] -= read();
rep(i, 1, n) G1[i].clear(), G2[i].clear(); // 清空
rep(i, 1, m) {
int t = read(), u = read(), v = read();
if (t == 1) G1[u].push_back(v), G1[v].push_back(u);
if (t == 2) G2[u].push_back(v), G2[v].push_back(u);
}
memset(id, 0, sizeof id); idcnt = 0;
rep(i, 1, n) if (!id[i]) G[++idcnt].clear(), sum[idcnt] = tag[idcnt] = col[idcnt] = 0, dfs(i); // 初始化+标记
rep(u, 1, n)
rep0(i, G1[u].size()) {
int v = G1[u][i];
if (id[u] == id[v]) tag[id[u]] = 1; else G[id[u]].push_back(id[v]);
}
int ans = 1;
rep(i, 1, idcnt) {
if (col[i]) continue; // 染过色直接跳过
ll white = 0, black = 0; int flag = 0;
col[i] = 1;
if (paint(i, white, black, flag)) { // 染色成功
if (flag) { if ((white ^ black) & 1) { ans = 0; break; } } // 有(2)情况判断差是否为偶数
else if (white != black) { ans = 0; break; } // 没有就判断是否相等
} else if ((white ^ black) & 1) { ans = 0; break; } // 不成功判断差是否为偶数
}
printf("%s
", ans ? "YES" : "NO");
}
return 0;
}