Resource:《Introduction to Evolutionary Computing》
1. What is an evolutionary algorithm?
There are many different variants of evolutionary algorithms. The common underlying behind all these techniques is the same: given a population of individuals within some environment that has limited resources, competition for those resources causes natural selection (survival of the fittest)
2. Components of Evolutionary Algorithms
- Representation (definition of individuals)
- Evalution function (or fitness function)
- Population
- Parent selection mechanism
- Variation operators, recombination and mutation
- Survivor selection mechanism (replacement)
- Initialisation procedure
- Termination condition
The general scheme of an evolutionary algorithm as a flowchart:
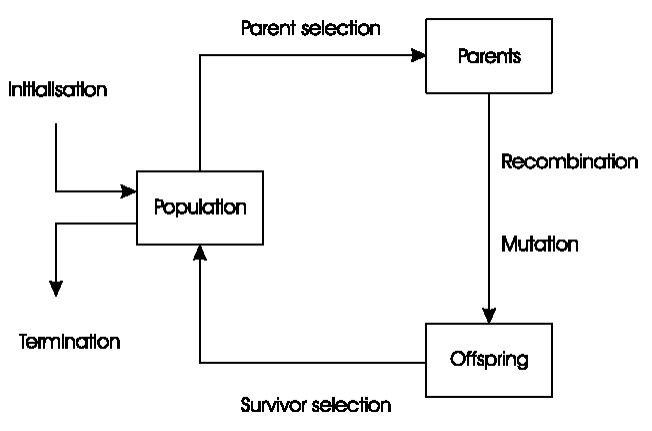
The general scheme of an evolutionary algorithm in pseudocode:

3. Genetic Algorithms
3.1 Introduction
This is commonly referred as a means of generating new candidate solutions.
This has:
- a binary representation
- fitness proportionate selection
- a low probability of mutation
- an emphasis on genetically inspired recombination as a means of generating new candidate solutions.
An introductory example: f(x) = x^2
3.2 Representation of Individuals
- binary representations
- integer representations
- real-valued or floating-point representation
- permutation representation
3.3 Mutation
- mutation for binary representations
- mutation operators for integer representations
- mutation operators for floating-point representations
- mutation operators for permutation representations
3.4 Recombination
- recombination operators for binary representations
- recombination operators for integer representations
- recombination operators for floating-point representations
- recombination operators for permutation representations
- multiparent recombination
3.5 Population models
- generational model
- steady-state model
generational model: In each generation we begin with a population of size μ, from which a mating pool of μ parents is selected. Next, λ (=μ) offspring are created from the mating pool by the application of variantion operators, and evaluated. After each generation, the whole population is replaced by its offspring, which is called the "next generation".
steady state model: The entire population is not changed at once, but rather a part of it. In this case, λ (<μ) old individuals are replaced by λ new ones, the offspring. The percentage of the population that is replaced is called the generational gap, and is equal to λ/μ. Usually, λ = 1 and a corresponding generation gap of 1/μ.
3.6 Parent Selection
- fitness proportional selection
- ranking selection
- implementing selection probabilities
- tournament selection
3.7 Survivor Selection
The survivor selection mechanism is responsible for managing the process whereby the working memory of the GA is reduced from a set of μ parents and λ offspring to produce the set of μ individuals for the next generation.
This step in the main evolutionary cycle is also called replacement.
age-based replacement
fitness-based replacement